【2024/3/12】汉诺塔问题C++

目录

题目

汉诺塔问题描述

图解（来源网络，仅供学习参考，权侵删）

本质思路：递归！

代码

---

题目

汉诺塔问题描述

汉诺塔（Hanoi Tower），又称河内塔，源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。问应该如何操作？

图解（来源网络，仅供学习参考，权侵删）

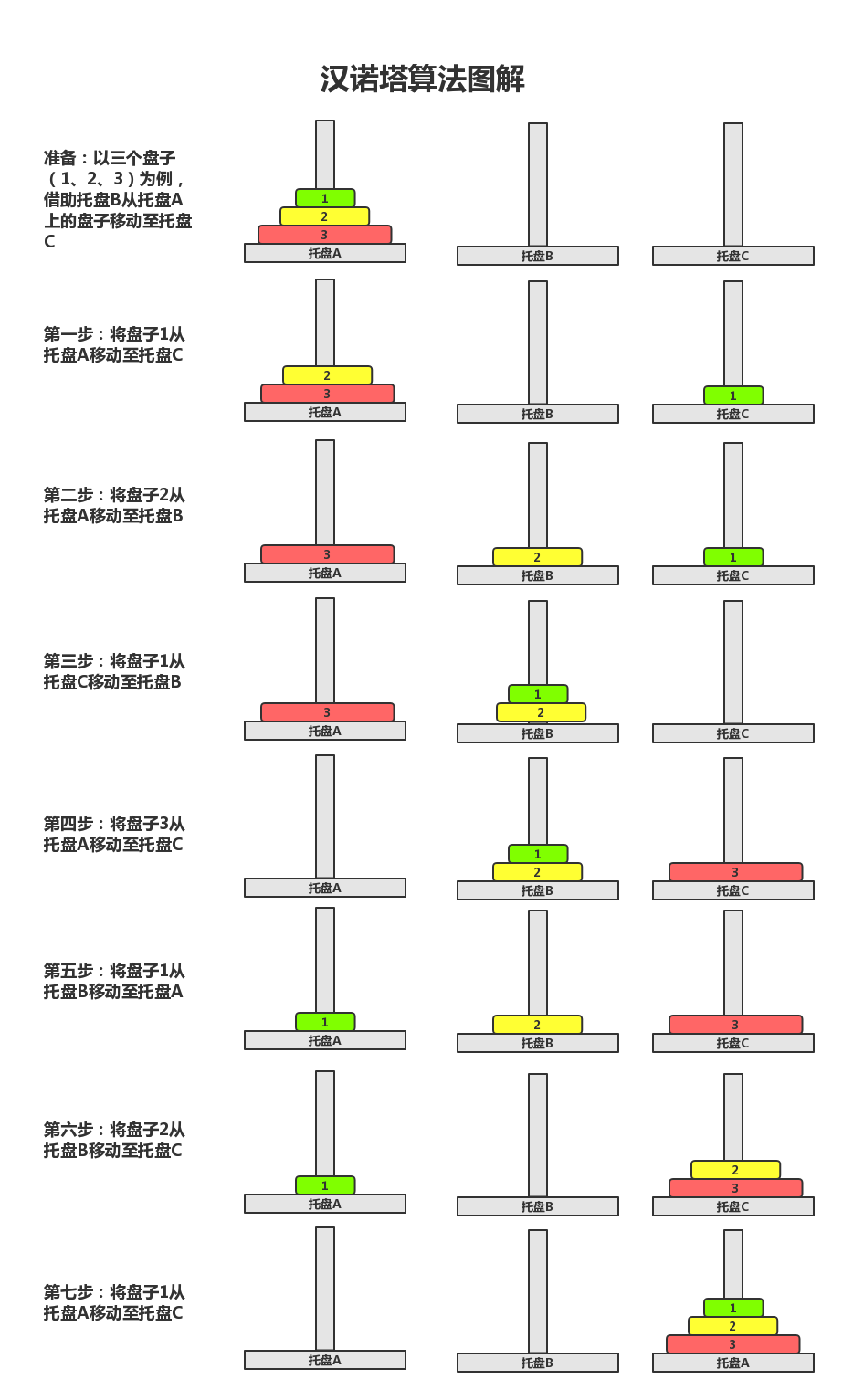
本质思路：递归！

注：理解不了，可以先去了解斐波那契数列来初步理解递归思想（斐波那契数列）https://blog.csdn.net/qq_62662919/article/details/128163754?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522171023830616800182750249%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=171023830616800182750249&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-128163754-null-null.142^v99^pc_search_result_base2&utm_term=%E6%96%90%E6%B3%A2%E9%82%A3%E5%A5%91%E6%95%B0%E5%88%97c%2B%2B&spm=1018.2226.3001.4187

解决递归问题我们三步走

1.明确目标函数功能，也就是你希望这个函数执行什么样的任务，例如：递归执行n！；

2.寻找递归结束条件，也就是参数为什么的时候，递归结束，例如：求解n！，即f(n)=n*(n-1),以n=2时是结束；

3.找出函数的等价关系式，例如斐波那契数列的两个等价式；

我们现在应当解答这三个问题，那么

1.功能：递归求解完成汉诺塔问题；

2.何时结束，自然是如图解一样，层数递减，减到最后剩一个（即n=1）时结束

如汉诺塔操作公式{ n==1  return 1;}

                             {n>1     f(n-1);    }、

3.等价式，上已给出。

 我以代码为实例解释

代码

第一种

​#include<bits/stdc++.h>//万能库，编译器当中可以使用#include<iostream>
using namespace std;
int count=0;//计数器，用于统计是第几步操作
int hanoi(int n,int a,int b,int c)//注意a，b，c仅为表达而已，一定要搞清楚实参是什么
{      // 盘数 起始1 目标3 暂存2
	if(n==1)//递归结束条件
	{
		count++;
		cout<<"第"<<count<<"步:盘子从"<<a<<"柱移至"<<b<<"柱"<<endl;
		return 0;
	}
	else//以下为递归操作，else本身是无需加入的，为简洁可去，该处为逻辑性故加
	{
		hanoi(n-1,a,c,b);
		count++;
		cout<<"第"<<count<<"步:盘子从"<<a<<"柱移至"<<b<<"柱"<<endl;
		hanoi(n-1,c,b,a);
	}
}
int main()
{
	int x;
	cin >> x;//输入层数
	hanoi(x,1,3,2);//调用函数
	return 0;
}

第二种，多加一个函数

#include<iostream>
#include<cstdio>
using namespace std;
void hanoi(int n,char A,char B,char C);///汉诺塔递归算法
void move(int n,char x,char y);///移动实现
int main(){
    int num;///要移动的盘子数
    cout<<"请输入要移动的盘子数：";
    cin>>num;
    hanoi(num,'A','B','C') ;
    return 0;
}
///具体实现
void hanoi(int n,char A,char B,char C){//n代表  A柱子上面的盘子数量

if(n==1){
    move(n,A,C);//如果只有一个盘子，直接从  A 移动到  C
}else{
    hanoi(n-1,A,C,B);//将 n-1个盘子从  A 移动到  B
    move(n,A,C);
    hanoi(n-1,B,A,C); //将 n-1个盘子从 B 移动到  C
}

}
void move(int n,char x,char y){
    printf("第%d个盘子从%c--->%c\n",n,x,y);
}