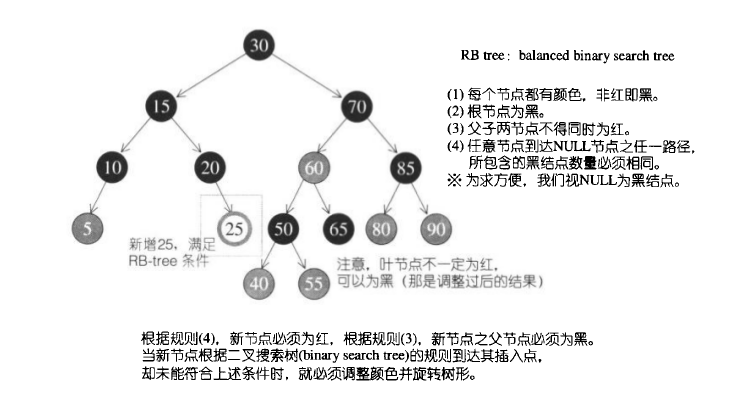
红黑树遵守的规则:一头(根)一脚(叶子节点)黑(黑色),黑同(从任意节点开始至NULL结点的黑色节点的个数相等)红不连(红色节点不能相连)
以下是红黑树的插入和旋转函数的简易实现:
#include <iostream>
#include <assert.h>
#include <string.h>
using namespace std;
typedef int Type;
typedef enum{RED=0, BLACK}Color; //节点的颜色
typedef struct Node{
Color color; //节点颜色
Type key; //节点的值
struct Node *left, *right, *parent; //左,右及父节点指针
}*PNode; //节点指针
//树的结构定义
typedef struct RB_TREE{
Node *root; //根结点
Node *Nil; //一个实现技巧,用于判断节点是否为空等
}RB_TREE;
Node *Buynode()
{
Node *p = new Node;
assert(p != NULL);
memset(p, 0, sizeof(Node));
return p;
}
//构造一个空树
void InitTree(RB_TREE &t)
{
t.Nil = Buynode();
t.root = t.Nil;
t.Nil->color = BLACK;
t.Nil->key = -1;
}
//左旋
void RotateLeft(RB_TREE &t, Node *p)
{
Node *s = p->right; //s为不平衡节点p的右树
p->right = s->left; //将s的左树挂接至p的右树
if(s->left != t.Nil){ //若s的左树不为空,就改变其左树的父节点
s->left->parent = p;
}
s->parent = p->parent; //改变s的父节点
if(p->parent == t.Nil){ //说明为p为根结点,旋转之后s为根结点
t.root = s;
}else if(p = p->parent->left){ //p之前位于左树就将s作为新的左树
p->parent->left = s;
}else{
p->parent->right = s; //否则s为p的父节点的右树
}
s->left = p; //p作s的左树
p->parent = s; //更改p的父节点
}
//右旋
void RotateRight(RB_TREE &t, Node *p)
{
Node *s = p->left;
p->left = s->right;
if(s->right != t.Nil){
s->right->parent = p;
}
s->parent = p->parent;
if(p->parent == t.Nil){
t.root = s;
}else if(p = p->parent->left){
p->parent->left = s;
}else{
p->parent->right = s;
}
s->right = p;
p->parent = s;
}
//调整树的平衡
void Insert_Fixup(RB_TREE &t, Node *z)
{
Node *y;
while(z->parent->color == RED){ //红红相连不平衡
if(z->parent == z->parent->parent->left){ //左侧插入
y = z->parent->parent->right; //y为插入节点的伯父节点
if(y->color == RED){
z->parent->color = BLACK;
z->parent->parent->color = RED;
y->color = BLACK;
z = z->parent->parent;
continue;
}else if(z == z->parent->right){ //左侧的内侧插入
z = z->parent;
RotateLeft(t, z); //左旋
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
RotateRight(t, z->parent->parent); //右旋
}else{ //右侧插入
y = z->parent->parent->left;
if(y->color == RED){
z->parent->color = BLACK;
z->parent->parent->color = RED;
y->color = BLACK;
z = z->parent->parent;
continue;
}else if(z == z->parent->left){ //右侧的内侧插入
z = z->parent;
RotateRight(t, z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
RotateLeft(t, z->parent->parent);
}
}
t.root->color = BLACK;
}
bool Insert(RB_TREE &t, Type x)
{
Node *p = t.Nil;
Node *s = t.root;
//找到合适的插入位置
while(s != t.Nil){
p = s;
if(x == s->key){
return false;
}else if(x < s->key){
s = s->left;
}else{
s = s->right;
}
}
//构造节点
Node *q = Buynode();
q->key = x;
q->parent = p;
//将节点插入树中的合适位置
if(p == t.Nil){ //则说明该树之前没有节点,则此节点为其根结点
t.root = q;
}else if(x < p->key){ //插入节点在节点p的左子树
p->left = q;
}else{ //插入节点在右子树
p->right = q;
}
//设置插入节点的信息
q->left = q->right = t.Nil;
q->color = RED;
//调整树的平衡
Insert_Fixup(t, q);
return true;
}
int main()
{
int ar[] = {100, 40, 6};
RB_TREE rb;
InitTree(rb);
int n = sizeof(ar) / sizeof(int);
for(int i = 0; i < n; ++i){
Insert(rb, ar[i]);
}
return 0;
}























 330
330

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








