算法的功能
对于任意上下文无关的文法消除左递归
问题分析
一、产生式直接消除左递归
形如
P→Pα|β
可以通过直接消除转化为:
P→βP′P′→αP′|ϵ
二、产生式间接消除左递归
有时候虽然形式上产生式没有递归,但是因为形成了环,所以导致进行闭包运算后出现左递归,如下:
S→Qc|cQ→Rb|bR→Sa|a
虽不具有左递归,但S、Q、R都是左递归的,因为经过若干次推导有
- SQcRbcSabc
- QRbSabQcab
- RSaQcaRbca
就显现出其左递归性了,这就是间接左递归文法。
消除间接左递归的方法是:
把间接左递归文法改写为直接左递归文法,然后用消除直接左递归的方法改写文法。
如果一个文法不含有回路,即形如PP的推导,也不含有以ε为右部的产生式,那么就可以采用下述算法消除文法的所有左递归。
消除左递归算法:
- (1) 把文法G的所有非终结符按任一顺序排列,例如,A1,A2,…,An。
- (2)
for (i=1;i<=n;i++)
for (j=1;j<=i-1;j++)
{ 把形如Ai→Ajγ的产生式改写成Ai→δ1γ /δ2γ /…/δkγ
其中Aj→δ1 /δ2 /…/δk是关于的Aj全部规则;
消除Ai规则中的直接左递归;
}
- (3) 化简由(2)所得到的文法,即去掉多余的规则。
利用此算法可以将上述文法进行改写,来消除左递归。
首先,令非终结符的排序为R、Q、S。对于R,不存在直接左递归。把R代入到Q中的相关规则中,则Q的规则变为Q→Sab/ ab/ b。
代换后的Q不含有直接左递归,将其代入S,S的规则变为S→Sabc/ abc/ bc/ c。
此时,S存在直接左递归。在消除了S的直接左递归后,得到整个文法为:
S→abcS′|bcS′|cS′S′→abcS′|εQ→Sab|ab|bR→Sa|a
可以看到从文法开始符号S出发,永远无法达到Q和R,所以关于Q和R的规则是多余的,将其删除并化简,最后得到文法G[S]为:
S→abcS′|bcS′|cS′S′→abcS′|ε
当然如果对文法非终结符排序的不同,最后得到的文法在形式上可能不一样,但它们都是等价的。例如,如果对上述非终结符排序选为S、Q、R,那么最后得到的文法G[R]为:
R→bcaR′|caR′|aR′R′→bcaR′|ε
容易证明上述两个文法是等价的。
代码实现
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <string>
#include <vector>
#include <queue>
#include <cctype>
#include <map>
#include <set>
#define MAX 507
using namespace std;
class WF
{
public:
string left;
set<string> right;
WF ( const string& temp )
{
left = temp;
right.clear();
}
void print ( )
{
printf ( "%s::=" , left.c_str() );
set<string>::iterator it = right.begin();
printf ( "%s" , it->c_str());
it++;
for ( ; it!= right.end() ; it++ )
printf ( "|%s" , it->c_str() );
puts("");
}
void insert ( const string& temp )
{
right.insert(temp);
}
};
map<string,int> VN_dic;
vector<WF> VN_set;
string start;
bool used[MAX];
void remove1 ( )
{
for ( int i = 0 ; i < VN_set.size() ; i++ )
for ( int j = 0 ; j < i ; j++ )
{
vector<string> cont;
set<string>& right1 = VN_set[i].right;
set<string>& right2 = VN_set[j].right;
char ch = VN_set[j].left[0];
set<string>::iterator it1 = right1.begin();
set<string>::iterator it2;
for ( ; it1 != right1.end() ; it1++ )
if ( it1->at(0) == ch )
for ( it2 = right2.begin() ; it2 != right2.end() ; it2++ )
cont.push_back ( *it2 + it1->substr(1) );
int nn = right1.size();
while ( nn-- )
{
if ( right1.begin()->at(0) == ch )
right1.erase ( right1.begin() );
else
{
cont.push_back ( *right1.begin() );
right1.erase ( right1.begin() );
}
}
for ( int i = 0 ; i < cont.size() ; i++ )
right1.insert ( cont[i] );
}
#define DEBUG
#ifdef DEBUG
for ( int i = 0 ; i < VN_set.size() ; i++ )
VN_set[i].print();
#endif
}
void remove2 ( )
{
for ( int i = 0 ; i < VN_set.size() ; i++ )
{
char ch = VN_set[i].left[0];
set<string>& temp = VN_set[i].right;
set<string>::iterator it = temp.begin();
string tt = VN_set[i].left.substr(0,1)+"\'";
bool flag = true;
for ( ; it != temp.end() ; it++ )
if ( it->at(0) == ch )
{
VN_set.push_back ( WF(tt));
VN_dic[tt] = VN_set.size();
flag = false;
break;
}
int x = VN_dic[tt]-1;
if ( flag ) continue;
vector<string> cont;
set<string>& ss = VN_set[x].right;
ss.insert ( "~" );
while (!temp.empty())
{
if ( temp.begin()->at(0) == ch )
ss.insert(temp.begin()->substr(1)+tt);
else
{
cont.push_back (temp.begin()->substr(0)+tt);
}
temp.erase(temp.begin());
}
puts ("");
for ( int i = 0 ; i < cont.size() ; i++ )
{
temp.insert ( cont[i] );
}
}
#define DEBUG
#ifdef DEBUG
for ( int i = 0 ; i < VN_set.size() ; i++ )
VN_set[i].print();
#endif
}
void dfs ( int x )
{
if ( used[x] ) return;
used[x] = 1;
set<string>::iterator it = VN_set[x].right.begin();
for ( ; it != VN_set[x].right.end(); it++ )
for ( int i = 0 ; i < it->length() ; i++ )
if ( isupper(it->at(i)) )
{
if ( it->length() > i+1 && it->at(i+1) == '\'' )
dfs ( VN_dic[it->substr(i,2)]-1 );
else
dfs ( VN_dic[it->substr(i,1)]-1 );
}
}
void simplify ( )
{
memset ( used , 0 , sizeof ( used ) );
int x = VN_dic[start]-1;
dfs ( x );
puts ( "finish" );
vector<WF> res;
for ( int i = 0 ; i < VN_set.size() ; i++ )
if ( used[i] )
res.push_back ( VN_set[i] );
VN_set.clear();
VN_set = res;
}
void print ()
{
puts("**********消除左递归后的结果********");
for ( int i = 0 ; i < VN_set.size() ; i++ )
VN_set[i].print();
puts("");
}
int main ( )
{
char buf[MAX];
int n;
VN_dic.clear();
VN_set.clear();
start="S";
puts ("请输入文法G[S]的产生式数量");
while ( ~scanf ("%d" , &n ) )
{
scanf ( "%d" , &n );
while ( n-- )
{
scanf ( "%s" , buf );
int len = strlen ( buf ),i;
for ( i = 0 ; i < len ; i++ )
if ( buf[i] == ':' )
{
buf[i] = 0;
break;
}
string temp = buf;
if ( !VN_dic[temp] )
{
VN_set.push_back ( WF(temp));
VN_dic[temp] = VN_set.size();
}
int x = VN_dic[temp]-1;
temp = buf+i+3;
VN_set[x].insert(temp);
}
remove1();
remove2();
simplify();
print();
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
测试
测试样例:
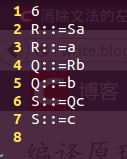
测试结果:
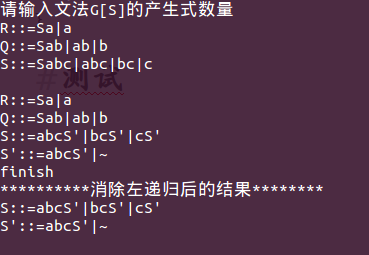
























 3357
3357

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








