Back Tracking(回溯法)

定义： 问题的解决方案定义为一个 n 元组：(x1, x2, …, xn)，其中 xi 取自有限集 Si。 一般来说，我们需要：
a. 找到最大化（或最小化）特定目标函数 P(x1, x2, …, xn) 的向量。
b. 找到满足特定标准函数 P(x1, x2, …, xn) 的（或所有）向量。
约束(Constraints)：
显式约束： 约束每个分量 xi 的值；所有满足显式约束的元组构成一个可能的解空间。
隐式约束： 组件间约束；隐式约束识别那些在解空间中满足标准函数的约束。

8-Queen problem

问题描述： 将 8 个皇后放在 8×8 棋盘上，使它们中的任何两个都不冲突，即它们中的任何两个都不位于同一行、列或对角线上。
用 1 到 8 标记行和列，还有皇后。
示例：

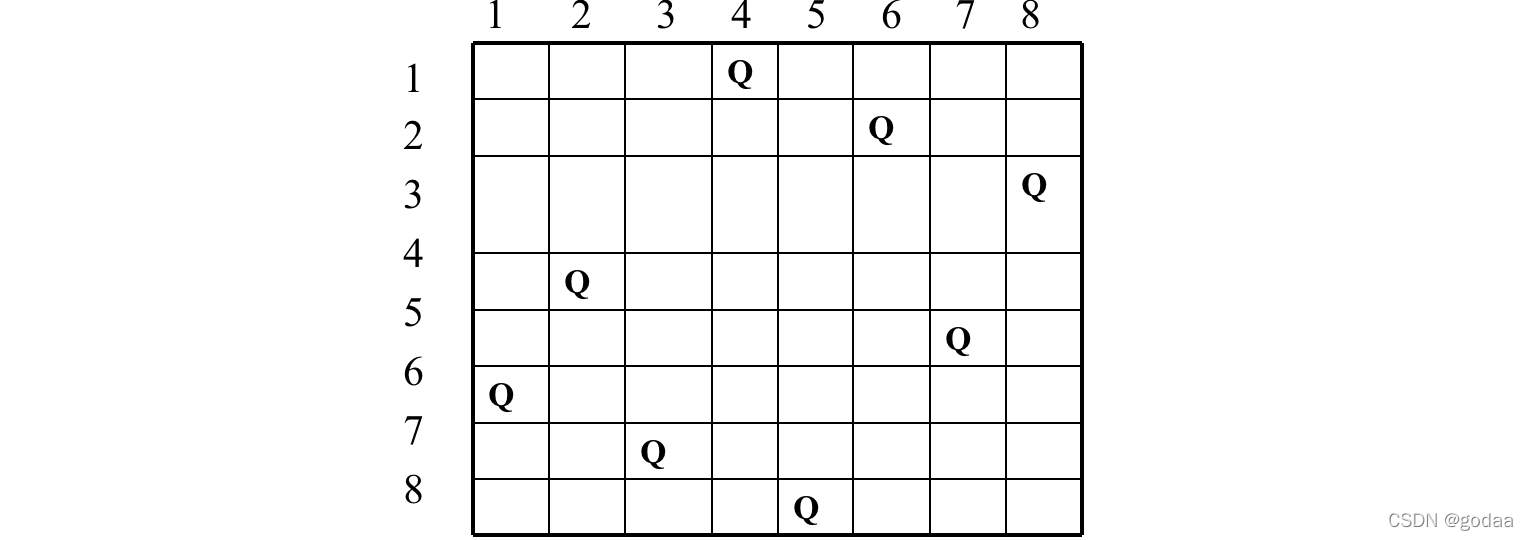
假设女王 i 位于第 i 行。
解可以定义为一个 8 元组 (x1, x2, …, x8)，其中 xi 是皇后 i 的列号。
上面的解是(4，6，8，2，7，1，3，5)。
显式约束： xi ∈ Si，Si={1,2,3,4,5,6,7,8}, 1≤ i≤ 8。解空间由 8^8 个 8 元组组成。
隐式约束： 它们中的任何两个都不位于同一行、同一列（任意两个 xi 不同）或对角线。
解空间由从根到每个叶子的所有路径组成，例如（4，2，3，1）。
问题状态： 树中的每个节点在解决问题时标识一个问题状态。
状态空间： 从根到每个节点的所有路径
解决方案状态： 那些问题状态，从根的路径标识解决方案空间中的向量（满足显式约束）。
答案状态： 那些从根的路径标识答案的解决方案状态(满足隐式约束)
状态空间树：

回溯法解决问题的方式： DFS
流程图：

在状态空间树中搜索：

1. 基本概念
   活节点：一个已生成的节点，其子节点尚未全部生成。
   E-node：当前正在生成其子节点的节点。
   死节点：所有儿子都已生成或不需要生成儿子的节点。
2. 以 DFS 方式生成问题状态
   E节点R的子C一旦生成，生成的子C就成为新的E节点，节点C在所有以节点C为根的树都被检查后，节点R将再次成为E节点。
   
   一个 E 节点一直是 E 节点，直到它变成一个死节点。
   回溯法的伪代码:
   
   T(X(1),…,X(k-1)) ： 返回所有可能的 X(k) ，给定 X(1),…,X(k-1)。
   B(X(1),…,X(k))： 返回 X(1),…,X(k) 是否满足隐式约束。
   第一个if: 是否有没有为当前节点生成的子。这里使用了bound function(限界函数）。
   第二个if: 判断是否为答案状态，是则输出
   第三个if: DFS方式，让新生成的节点成为 E 节点。
   else: 所有的儿子都被检查过，回溯。
   N Queen 伪代码：

Bound function:
   

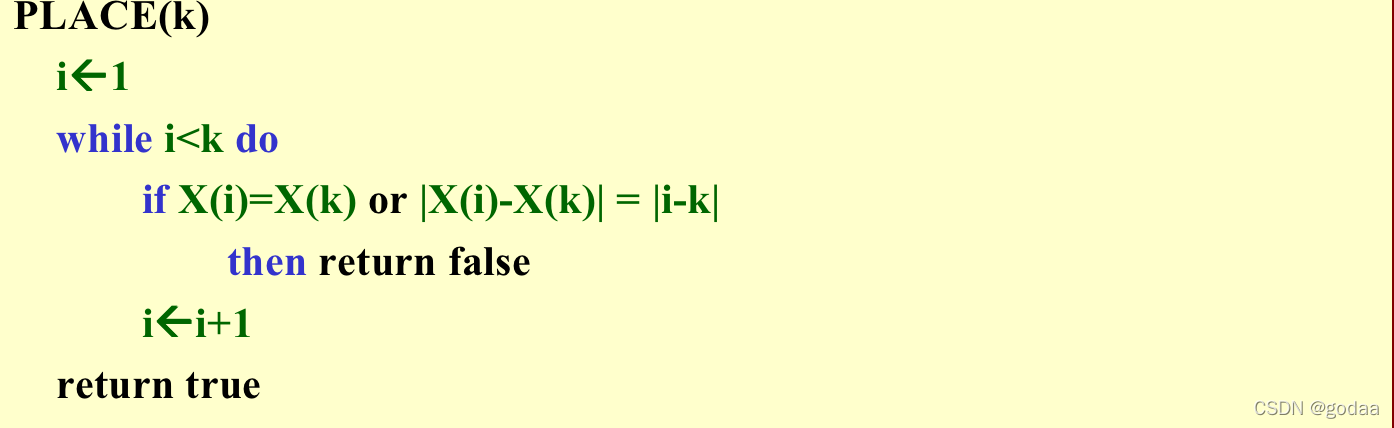
Subset-sum problem

问题描述： 给定n+1个正整数：wi，1≤i≤n，M，求出W={wi}的所有子集，其中汇总等于M。
例如。 n＝4，(wl，w2，w3，w4)＝(11，13，24，7)，M＝31
预期的子集是（11，13，7）和（24，7）。
解决方案形式：
子集和问题的解定义为一个 n 元组 (x1，x2，… ，xn)，其中 xi∈ {0，1}, 1≤i≤n。 如果wi包含在子集中，则xi＝1，否则xi＝0。
以上答案可以定义为（1，1，0，1）和（0，0，1，1）。
状态空间树：

很容易确定 X(i)/生成问题状态。
Bound function:

判断一个branch是否是应该被放弃，需测试条件，假设在level k 积累到的和为S,由于所有的权重都是事先排好序的，也即从小到大，所以如果S+wk+1>M,那么显然再沿着这条branch下去不可能得到一个可行解，只要还有能够找到的可能性，即如果S+∑wi(i=k+1~n)<=M,就沿着这个branch下去。两种情况综合起来就是限界函数。
伪代码：

其中,S=∑wi(I=1 ~ k-1)xi , r = ∑wi(I=k ~ n)
Initial call: SUMOFSUB(0,1,∑wi(i=1~n))
示例：
(w1, w2, w3, w4 ) = ( 5, 10 , 15, 20 ) ; M = 25

0-1 knapsack problem

问题描述： 小偷抢劫了一家商店，发现了 n 件物品，其中物品 i 的价值为 $pi，重量为 wi 磅，小偷最多可以在他的背包中携带 M ∈ N但他想尽可能多地装载有价值的物品。 他应该怎么选择？
定义解的形式为： 一个解定义为一个 n 元组 (x1，x2，… ，xn)，其中 xi∈{0，1}, 1≤i≤n。 如果第 i 项被取走，则 xi＝1，否则 xi＝0。
需要注意的是：这是一个优化问题，我们会找到一个最佳答案，而不是可行的答案。
状态空间树：

Bound function:

如果右边描述的方法返回的利润大于现在获得的利润则继续搜索。
伪代码：