二叉树的递归实现（前序，中序，后序，层序，高度，叶子节点数，第k层节点数）

一：二叉树是我们学过最常用也是最基础的数据结构，要想学好二叉树

①首先要学会利用含有非法值得数组前序遍历★建立一颗二叉树；

②然后我们要会用递归的方式对这颗二叉树进行★前序，★中序，★后序的遍历打印，也要学会利用队列的先进先出的原则对着棵树进行★层序访问；

③然后我们还要知道这颗二叉树的基本信息；比如，★二叉树的总节点个数，★二叉树的叶子节点个数，★二叉树的第k层的节点个数，★二叉树的高度（深度）；
二：完整代码

#include<iostream>
using namespace std;
#include<assert.h>
#include<queue>

template<class T>
struct TreeNode
{
    TreeNode( const T& data=T())
        :_data(data)
        ,_left(NULL)
        ,_right(NULL)
    {}
    int _data;
    TreeNode<T>* _left;
    TreeNode<T>* _right;
};

template<class T>
class BinaryTree 
{
    typedef  TreeNode<T>  Node;
public:
    BinaryTree()//无参构造函数
        :_root(NULL)
    {}
    BinaryTree(const T* arr,int sz,const T invalid)//有参构造函数
    {
        assert(arr);
        int index=0;//数组中的位置
        _root=BuildTree(arr,sz,invalid,index);
    }
    BinaryTree(const BinaryTree<T>& bt)//拷贝构造
    {
        _root=Copy(bt._root);
    }
    BinaryTree<T>&  operator=(const BinaryTree<T>& bt)//赋值运算符重载1
    {
        if (this!=&bt)
        {
            Node* tmp=Copy(bt._root);//拷贝源对象给中间变量
            Free(_root);//释放本对象
            _root=tmp;//将中间变量给本对象
        }
        return  *this;
    }
    //BinaryTree<T>&  operator=(const BinaryTree<T>& bt)//赋值运算符重载2（现代写法）
    //{
    //       std::swap(_root,bt._root);
    //  return *this;
    //}
    void PreOrder()//前序遍历打印（递归）
    {
        cout<<"前序打印:";
        _PreOrder(_root);
    }
    void InOrder()//中序遍历打印（递归）
    {
        cout<<"中序打印:";
        _InOrder(_root);
    }
    void EndOrder()//后序遍历打印（递归）
    {
        cout<<"后序打印:";
        _EndOrder(_root);
    }
    void SeqOrder()//层序遍历打印
    {
        cout<<"层序打印:";
        _SeqOrder(_root);
    }
    int Szie()//二叉树节点数
    {
        return _Szie(_root);

    }
    int Hight()//二叉树的高度
    {
        return _Hight(_root);
    }
    int  GetLeafNodeNumber()//求叶子节点数
    {
        return _GetLeafNodeNumber(_root);
    }
    int Get_K_NodeNumber(int k)//求第k层节点数
    {
        return _Get_K_NodeNumber(_root,k);
    }
protected:  
    Node* BuildTree(const T*arr,int sz,const T& invalid, int& index)//前序遍历建树
    {
        assert(arr);
        if (index<sz && arr[index]!=invalid)
        {
            Node* root=new Node(arr[index]);
            root->_left=BuildTree(arr,sz,invalid,++index);
            root->_right=BuildTree(arr,sz,invalid,++index);
            return root;
        }
        return NULL;
    }
    Node* Copy(Node* root)//先序遍历拷贝(递归)
    {
        Node* tmp=NULL;
        if (root)
        { 
            tmp=new Node(root->_data);
            tmp->_left=Copy(root->_left);
            tmp->_right=Copy(root->_right);
        }
        return tmp;
    }
    void Free(Node*& root)//后序遍历的方式释放树
    {
        if (root)
        {
            Free(root->_left);
            Free(root->_right);
            delete  root;
            root=NULL;
        }

    }
    void _PreOrder(Node* root)//前序遍历打印
    {
        if (root)
        {
            cout<<root->_data<<"->";
            _PreOrder(root->_left);
            _PreOrder(root->_right);
        }

    }
    void _InOrder(Node* root)//中序遍历打印
    {
        if (root)
        {       
            _InOrder(root->_left);
            cout<<root->_data<<"->";
            _InOrder(root->_right);
        }

    }
    void _EndOrder(Node* root)//后续遍历打印
    {
        if (root)
        {
            _EndOrder(root->_left);
            _EndOrder(root->_right);
            cout<<root->_data<<"->";
        }

    }
    void _SeqOrder(Node* root)//层序遍历打印
    {
        //利用队列先进先出的特点层序的打印二叉树的节点
        queue<Node*> q;
        if (root)//首先判断树的跟目录不为空
        {
            q.push(root);//将根目录入队列
        }
        while (!q.empty())//当队列不为空时，此时队列中一直有元素，则继续进入循环打印
        {
            Node* tmp=q.front();
            cout<<tmp->_data<<"->";
            q.pop();
            if (tmp->_left)
            {
                q.push(tmp->_left);
            }
            if (tmp->_right)
            {
                q.push(tmp->_right);
            }
        }

    }
    int _Szie( Node* root)//二叉树节点数
    {
        int count=0;//定义一个count计数器
        if (NULL==root)//情况一：如果root为空，则节点数为0
        {
            count=0;
        }
        else//情况二：root不为空
        {
            //树的节点=左子树的节点数+右子树的节点数+1（根）；
            count=_Szie(root->_left)+_Szie(root->_right)+1;
        }
        return count;
    }
    int _Hight(Node* root)//二叉树的高度
    {

        if (NULL==root)//情况一：root为空
        {
            return 0;
        }
        //情况二：root不为空,此时该树高度为左右子树中大的树高度+1（根）
        return _Hight(root->_left)>_Hight(root->_right)? 
              (_Hight(root->_left)+1):(_Hight(root->_right)+1);

    }
    int _GetLeafNodeNumber(const Node* root)//二叉树的叶子节点数
    {   
        if (NULL==root)//情况一：root为空
        {
            return 0;
        }
        if (NULL==root->_left && NULL==root->_right)//情况二：该节点左右子树都为空
        {
            return 1;
        }
        //情况三：左右子树都不为空

        return _GetLeafNodeNumber(root->_left)+_GetLeafNodeNumber(root->_right); 
    }
    int _Get_K_NodeNumber(Node* root,int k)//求二叉树的第k层的
    {
        assert(k>0);        
        if (NULL==root)
        {
            return 0;
        }
        if (k==1)
        {
            return 1;
        }
        return _Get_K_NodeNumber(root->_left,k-1)+_Get_K_NodeNumber(root->_right,k-1);  
    }
protected:
    Node*  _root;
};

测试代码：

void Test()
{
    /*int arr[]={1,2,'#',3,'#','#',4,5,'#',6,'#',7,'#','#',8};*/
    int arr[] = {1, 2, 3, '#', '#', 4, '#' , '#', 5, 6,'#','#','#'};
    int sz=sizeof(arr)/sizeof(arr[0]);
    BinaryTree<int>  bt2(arr,sz,'#');//调用带有参数的构造函数
    BinaryTree<int>  bt1(bt2);//调用拷贝构造函数
    BinaryTree<int>  bt;//调用默认构造函数
    bt=bt1;//调用赋值运算符重载
    bt.PreOrder();
    cout<<endl;
    bt.InOrder();
    cout<<endl;
    bt.EndOrder();
    cout<<endl;
    bt.SeqOrder();
    cout<<endl;
    cout<<"二叉树的节点数："<<bt.Szie()<<endl;
    cout<<"二叉树的叶子节点个数:"<<bt.GetLeafNodeNumber()<<endl;
    cout<<"二叉树的高度:"<<bt.Hight()<<endl;
    cout<<"二叉树第1层节点数："<<bt.Get_K_NodeNumber(1)<<endl;
    cout<<"二叉树第2层节点数："<<bt.Get_K_NodeNumber(2)<<endl;
    cout<<"二叉树第3层节点数："<<bt.Get_K_NodeNumber(3)<<endl;
    cout<<"二叉树第4层节点数："<<bt.Get_K_NodeNumber(4)<<endl;
    cout<<"二叉树第5层节点数："<<bt.Get_K_NodeNumber(5)<<endl;


}
int main()
{
    Test();
    return 0;
}

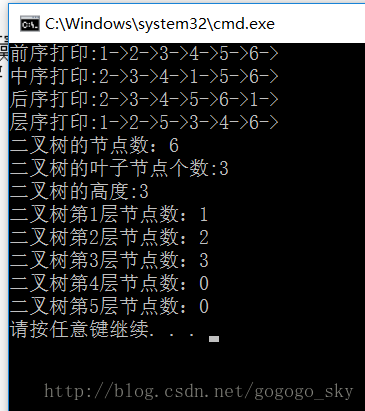
三：运行结果

后面还有二叉树的非递归实现。。。敬请关注 ——-O(∩_∩)O哈哈~