《剑指offer》:[25]二叉树中和为某一值的路径

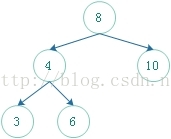
题目：输入一棵二叉树和一个整数，打印出二叉树中结点值的和为输入整数的所有路径。从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。

分析如下：

例如上图和整数18。第一条路径8,4,6。第二条路径8,10。
这里需要明确一个概念：路径就是从根节点出发到叶子结点。一定是到叶子结点结束，而不是中间的某个结点。
这就要求我们需要从根节点开始遍历，前中后三种遍历中也只有前序遍历是首先访问根节点。
因为这里的访问存在回溯的问题，因为我们需要遍历完所有的路径，这里就需要我们保存以访问的结点信息。然后在回溯的时候我们就能明确的知道此事处于何地，进退有序。

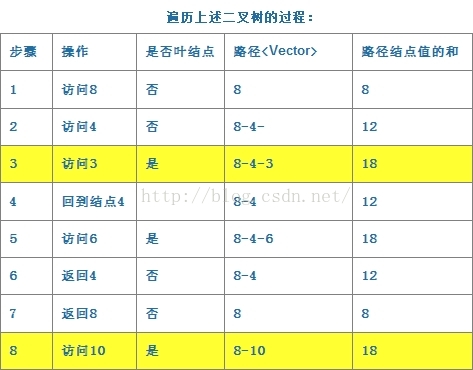
遍历的过程如下图所示：

具体实现代码如下：

#include <iostream>
#include <vector>
using namespace std;
struct BinartyTree
{
	int data;
	BinartyTree *pLeft;
	BinartyTree *pRight;
};
BinartyTree *pRoot1=NULL;
int arr[5]={8,4,10,3,6};
vector <int> path;
void Loop(BinartyTree **root,int data);
void CreateTree(BinartyTree**root,int *array,int lenght);
void FindPath(BinartyTree *tree,int expectionSum);
void FindPathhelp(BinartyTree *tree,int expectedSum,vector<int> &paths,int currentSum);

void CreateTree(BinartyTree**root,int *array,int lenght)
{
	for(int i=0;i<lenght;i++)
		Loop(root,array[i]);
}
void Loop(BinartyTree **root,int data)
{
	BinartyTree *pNode=new BinartyTree;
	pNode->data=data;
	pNode->pLeft=pNode->pRight=NULL;
	if(NULL==*root)
		*root=pNode;
	else
	{
		BinartyTree *back=NULL;
		BinartyTree *current=*root;
		while(current)
		{
			back=current;
			if(current->data>data)
				current=current->pLeft;
			else
				current=current->pRight;
		}
		if(data > back->data)
			back->pRight=pNode;
		else
			back->pLeft=pNode;
	}
}

void PreOrder(BinartyTree *tree)
{
	BinartyTree *temp=tree;
	if(temp)
	{
		cout<<temp->data<<" ";
		PreOrder(temp->pLeft);
		PreOrder(tree->pRight);
	}
}
void FindPathhelp(BinartyTree *tree,int expectedSum,vector<int> &paths,int currentSum)
{
	currentSum+=tree->data;
	paths.push_back(tree->data);
	bool isleaf=NULL==tree->pLeft && NULL ==tree->pRight;
	if(currentSum==expectedSum && isleaf) //如果找到，则打印出路径结果；
	{
		cout<<"The path is found:"<<endl;
		vector<int>::iterator iter;
		for(iter=path.begin();iter!=path.end();iter++)
			cout<<*iter<<" ";
		cout<<endl;
	}
	//如果不是叶子结点，则遍历它的子结点；
	if(tree->pLeft !=NULL)
		FindPathhelp(tree->pLeft,expectedSum,paths,currentSum);
	if(tree->pRight !=NULL)
		FindPathhelp(tree->pRight,expectedSum,paths,currentSum);
	//返回到父结点之前，在路径上删除当前的结点；
	paths.pop_back();
}
void FindPath(BinartyTree *tree,int expectionSum)
{
	if(NULL==tree)
		return;
	int currentSum=0;
	FindPathhelp(tree,expectionSum,path,currentSum);
}

int main()
{
	CreateTree(&pRoot1,arr,5);
	FindPath(pRoot1,18);
	system("pause");
	return 0;
}

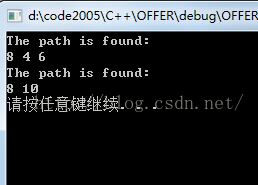
运行结果：

小结：当我们遇到一个问题无从下手的时候，我们可以举一个实际简单的例子，这样可以很快的帮我们理清思路，找到规律，然后再将其推向一般化。当我们遇到复杂的问题的时候，我们可以采取“各个击破”的军事思想，这种思想的精髓是当敌我悬殊时，我们可以把强大的敌人分割开来，然后集中优势兵力打被分隔开的小股力量，各个击破。那么我们在解决问题的时候，我们就可以把问题化简为单个的小问题，然后逐个解决小问题，这种“分治法”可能会使问题容易很多。