题目:从上往下打印二叉树
此题实质是考察树的遍历算法,只是这种遍历不是我们熟悉的前、中、后序遍历,而是我们的层次遍历。其实也很简单。分析如下:
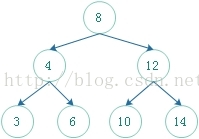
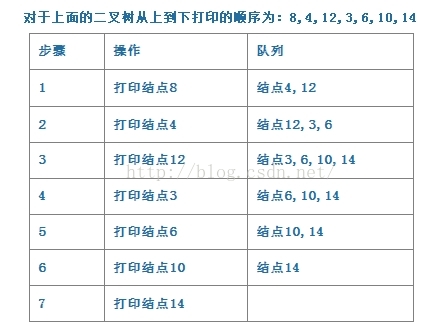
按层打印毫无疑问,我们需要从根节点开始,然后依次打印其子节点,为了能保证能打印其子节点,我们应该先保存其两个子节点。如上图先打印根结点8,然后保存其
左右结点4,12;然后再打印4,接着将3,6结点依次放入容器中;接着结点12,依次往下...很明显这是一个队列结构。所以我们可以借助一个队列来完成。
其实现代码如下:
此题实质是考察树的遍历算法,只是这种遍历不是我们熟悉的前、中、后序遍历,而是我们的层次遍历。其实也很简单。分析如下:
按层打印毫无疑问,我们需要从根节点开始,然后依次打印其子节点,为了能保证能打印其子节点,我们应该先保存其两个子节点。如上图先打印根结点8,然后保存其
左右结点4,12;然后再打印4,接着将3,6结点依次放入容器中;接着结点12,依次往下...很明显这是一个队列结构。所以我们可以借助一个队列来完成。
其实现代码如下:
#include <iostream>
#include <deque>
#include <queue>
using namespace std;
struct BinaryTree
{
int data;
BinaryTree *pLeft;
BinaryTree *pRight;
};
BinaryTree *pRoot1=NULL;
deque<BinaryTree*> d1;
int arr[7]={8,4,12,3,6,10,14};
void InsertTree(BinaryTree *root,int data);
void CreateTree(BinaryTree **root,int *array,int length);
void PrintFronTopToBottom(BinaryTree *root);
void InsertTree(BinaryTree *root,int data)
{
if(root->data > data)
{
if(NULL==root->pLeft)
{
BinaryTree *pNode=new BinaryTree;
pNode->data=data;
pNode->pLeft=pNode->pRight=NULL;
root->pLeft=pNode;
}
else
InsertTree(root->pLeft,data);
}
else
{
if(NULL==root->pRight)
{
BinaryTree *pNode=new BinaryTree;
pNode->data=data;
pNode->pLeft=pNode->pRight=NULL;
root->pRight=pNode;
}
else
{
InsertTree(root->pRight,data);
}
}
}
void CreateTree(BinaryTree **root,int *array,int length)
{
for(int i=0;i<length;i++)
{
if(NULL==*root)
{
BinaryTree *pNode=new BinaryTree;
pNode->data=arr[i];
pNode->pLeft=pNode->pRight=NULL;
*root=pNode;
}
else
InsertTree(*root,arr[i]);
}
}
void PrintFronTopToBottom(BinaryTree *root)
{
if(!root)
return;
BinaryTree *temp=root;
d1.push_back(root);
while(d1.size())
{
temp=d1.front();
d1.pop_front();
cout<<temp->data<<" ";
if(temp->pLeft)
d1.push_back(temp->pLeft);
if(temp->pRight)
d1.push_back(temp->pRight);
}
}
int main()
{
CreateTree(&pRoot1,arr,7);
PrintFronTopToBottom(pRoot1);
//PreOrder(pRoot1);
cout<<endl;
system("pause");
return 0;
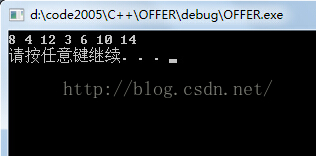
}运行结果:
























 73
73

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








