基于车头灯的PCANet车辆识别

基于PCANet的卷积神经网络架构用于车辆型号识别系统

摘要

车辆型号识别在智能交通系统中起着至关重要的作用。现有的大多数车辆型号识别方法主要集中在定位车辆图像中的大范围全局特征，或提取多个局部从属级特征。本文提出了一种基于主成分分析网络的卷积神经网络（PCNN），并聚焦于车辆的一个有区分性的局部特征——车头灯，用于车辆型号识别。所提模型无需精确地定位和分割车头灯。具体而言，PCNN证实了主成分分析（PCA）和CNN在从车头灯图像中提取层次特征以及降低传统CNN系统计算复杂度方面的有效性。为了进一步提升训练过程，同时保持网络的判别性，采用随机梯度下降优化的反向传播方法更新全连接层。所提方法在一个包含13300张训练图像和2660张测试图像的数据集上进行了验证。该模型对各种失真具有较强的鲁棒性。实验表明，PCNN在PLUS数据集上针对38个汽车品牌和车辆型号的平均准确率达到99.51%，优于当前最先进的技术。此外，所提方法在公开的CompCars数据集上也验证了其有效性，在357个车辆型号上实现了89.83%的准确率。

索引术语

主成分分析、卷积神经网络、反向传播、优化、随机梯度下降、车辆型号识别。

一、引言

车辆型号识别是智能交通系统（ITS）中的一项重要任务，该系统包括智能停车系统、交通流量分析、交通监控和电子收费。此外，在车辆识别中，车辆型号识别至关重要，因为在刑事案件中，车辆车牌和车辆标志经常被非法更换。因此，车辆车牌定位[1]–[3]和车辆型号识别同样重要，在提供车辆所有权信息以打击非法活动方面至关重要。此外，在获知车辆型号后，还可确定其物理尺寸或类型信息，例如轿车、微型面包车、运动型多用途汽车（SUV）等。随后，车辆型号及其类型信息可用于基于车辆类型的电子收费系统，从而最终优化交通流量。尽管车辆型号识别在智能交通系统领域具有重要意义，但此前大多数车辆识别研究集中在车牌识别[4]、车辆品牌识别[5]、车辆类型分类[6]，以及三维模型车辆类型分类[7],[8]。

除了上述已被广泛研究的传统课题外，车辆品牌与型号识别（VMMR）也是一项具有挑战性的任务，并且有很大的提升潜力。皮尔斯和皮尔斯[9]利用方映射梯度（SMG）或局部归一化Harris强度（LNHS）作为全局特征提取器，应用于图像象限，以朴素贝叶斯分类器进行车辆型号分类。尽管其分类准确率达到96%，但该方法在复杂环境（例如具有挑战性的视角和阴影条件）下仍然存在局限性。彼得罗维奇和库茨[10]通过对车辆前视图像的归一化结构提取特征，在77种车辆型号上获得了93%的准确率。Psyllos et al.[11]提出了一种基于尺度不变特征变换（SIFT）关键点的框架，用于提取VMMR的不变特征。然而，他们的框架无法为每张车辆图像提供具体的车辆型号。Hsieh et al.[12]采用对称加速稳健特征（SURF）作为特征提取器，以网格化方式检测多类别车辆品牌与型号。报告的平均准确率为99.07%，但该方法在不同视角和光照变化下表现不佳。Siddiqui et al. [13]提出了加速稳健特征包（BoSURF）和一种多类分类器支持向量机（SVM）系统用于车辆型号识别，报告了最高的平均准确率94.84%。然而，他们的方法在大范围的光照变化和非正面视角下仍然受限。Clady et al. [14]设计了一种基于定向轮廓点的框架用于车辆类型识别。通过采用三种投票算法和距离误差，该框架在50种车辆型号上实现了93.1%的准确率。张[15]研究了两种特征提取器，即Gabor小波变换和金字塔方向梯度直方图（PHOG），用于车辆类型分类。通过第二分类器集成增强了分类可靠性，从而达到了98.65%的准确率。上述VMMR中的一些方法仍受限于对手工设计特征（如SIFT）的强依赖性，这类方法效率低下，并且在应对视角变化、光照不足和噪声等各种失真时缺乏鲁棒性。

最近，一些研究人员在智能交通系统领域利用深度学习技术从低层到高层提取特征。高层特征基于堆叠可训练阶段进行提取，然后通过多类分类器进行分类。Dong et al.[16]采用半监督卷积神经网络（CNN）进行车辆类型分类。他们引入了稀疏拉普拉斯滤波器学习方法，并使用softmax分类器，实现了88.11%的准确率。Huang et al.[17]将主成分分析（PCA）作为CNN的预训练策略，以改进车辆标志识别的训练过程。他们在初始训练时间减少60倍的情况下，报告了99.07%的识别准确率。Yang et al.[18]针对每辆车的不同视角应用CNN进行车辆型号识别。Liu et al.[19]提出了一种深度相对距离学习（DRDL）方法，该方法采用双分支深度卷积神经网络将原始车辆图像投影到欧几里得空间，用于车辆再识别。Fang et al.[20]提出了一种由粗到细的CNN框架用于细粒度车辆型号识别。他们的框架从车辆图像的全局和局部区域中提取判别性和层次性特征。基于少量车辆区域（如整个前部、中心、左侧和右侧部分），他们在细粒度车辆型号识别任务上达到了98.29%的准确率。

尽管这些方法表现出优越的性能，但大多数方法依赖于车辆的多个部件来实现准确识别，因此可能极其耗时。局部区域特征，即前大灯和车牌，因其对环境变化具有鲁棒性[21]，在汽车型号识别中受到重视。根据我们的研究结果，识别任务可以仅关注车辆头灯的一侧，因为车辆前视图中间存在对称轴。值得注意的是，每个车辆型号的车头灯都具有判别性特征。此外，由于车头灯的物理尺寸小于其他部件（如格栅、保险杠、发动机罩等），其在识别系统中需要计算的参数更少。更重要的是，与车辆标志不同，车头灯几乎不可更换且很少被更换，从而使车辆识别更具有相关性。除此之外，人们经常提到，当未使用高性能图形处理器（GPU）进行并行计算时，CNN的训练过程所需时间将呈指数级增长。

为了解决上述问题，我们利用主成分分析（PCA）在生成卷积滤波器方面的优势，同时保留传统CNN的层次结构和判别性。与使用车辆大量全局和局部特征的方法不同，基于PCANet的卷积神经网络（PCNN）能够仅从车头灯学习到用于车辆型号识别的重要特征。由PCA卷积滤波器学习得到的特征图随后被输入到展平的全连接层中。用于分类。因此，我们省略并跳过了对通过主成分分析生成的卷积滤波器进行exhaustive反向传播（BP）训练的过程。此外，通过仅考虑车头灯进行车辆型号识别，计算成本大幅降低，同时并未牺牲其性能。本文工作的贡献总结如下：
- 提出了一种用于车辆型号识别的端到端PCNN框架，该框架可显著降低训练过程的计算代价，同时保持CNN的判别性。
- 提出了一种能够自动提取层次特征的方法，并且对车辆头灯图像中的各种失真具有鲁棒性，适用于车辆型号识别。
- 证明了简单而高效的粗分割技术足以准确定位车辆头灯的位置。因此，对于车辆型号识别而言，不再需要对全局或局部特征进行精确检测。

本文其余部分组织如下。基于主成分分析和卷积神经网络的车辆型号识别系统在第二节中进行说明。第三节展示了数据集、实验结果及分析。我们在第四节总结了本项工作。

II. 所提基于PCANet的CNN模型框架

A. 感兴趣区域的粗略分割

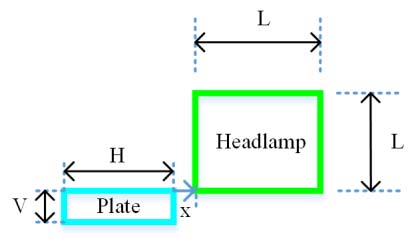
图1展示了所提出的利用粗分割技术的车辆头灯检测系统。如图1(a)所示，原始的车辆左前视图图像来自交通监控系统。这些原始图像首先被转换为8位分辨率的灰度图像，然后执行车牌定位（LPL）模块。LPL模块采用滑动同心窗口（SCW）分割方法、二值化处理，以及连通域标记和二值测量[22]。在LPL之后，车辆车牌的左上和右下坐标被确定，如图1中的红色点所示。LPL模块的输出是如图2中浅蓝色矩形框所示，尺寸为H × V的车牌区域。

根据图2，车头灯区域基于车辆车牌右上角的像素坐标进行粗略分割。经过LPL处理后，车头灯的左下角坐标被定义为从车牌右上角坐标水平平移x= 40像素得到的位置。本研究中采用较大尺寸为L × L的车辆前大灯分割区域，以适应不同车辆型号的前大灯，如图1(c)和图2中的绿色框所示。因此，车辆前大灯有很大概率位于该粗分割区域内。本研究仅考虑了38种车辆型号，未包含尺寸较大的车辆，即运动型多用途车（SUV）和四轮驱动（4WD）车辆。

B. 基于PCANet的CNN（PCNN）

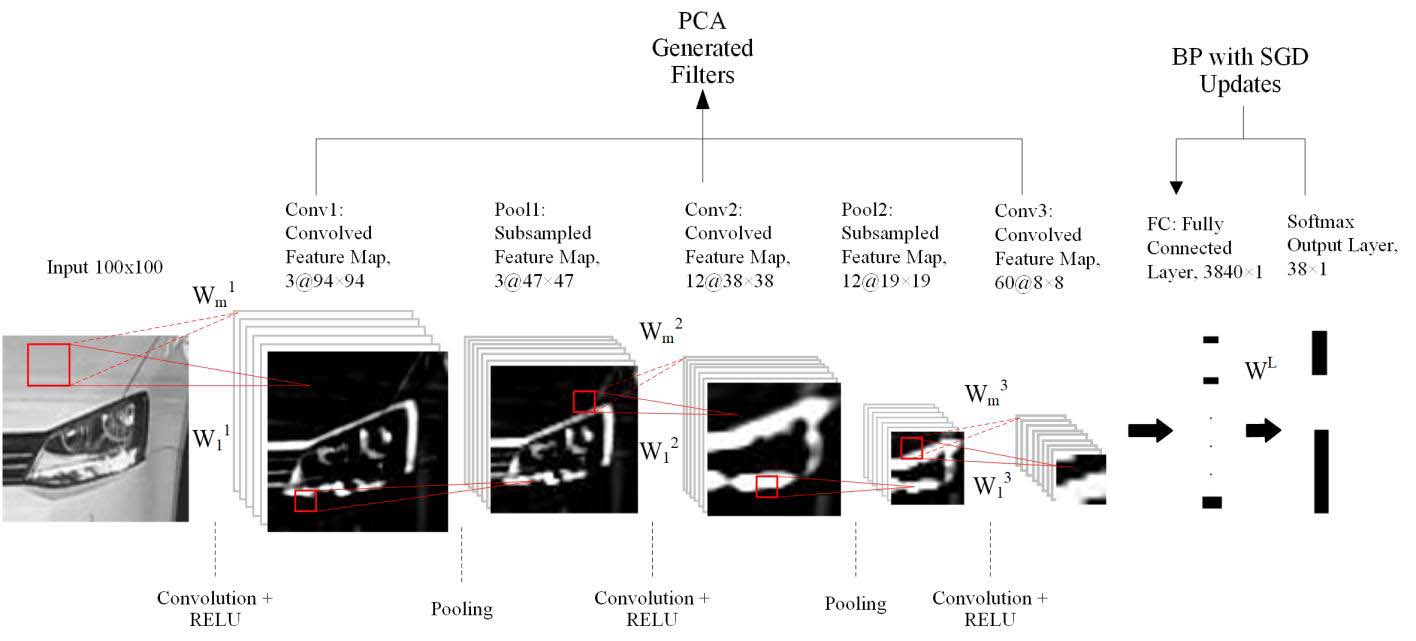
基于PCANet的卷积神经网络结构如图3所示。PCNN是一个端到端系统，其输入为粗分割的尺寸为100 × 100像素的车头灯图像，输出为车辆型号类别预测。PCANet能够学习图像中的非线性关系，因此对噪声具有鲁棒性。此外，PCANet具有低计算成本，并且在适应各种条件方面表现出优越性[23]–[25]。PCANet是一种基于以下三个部分的图像分类网络：1）主成分分析（PCA）用于学习多级滤波器组；2）二值哈希；3）分块直方图。为了降低计算成本，所提出的PCNN利用PCA来学习卷积滤波器。与PCANet不同的是，PCNN采用了非线性激活、池化层和全连接层，不仅能够提取判别性特征，还能提供平移、旋转、缩放等不变性。在PCNN中，各卷积层Conv1、Conv2和Conv3的输入分别为前大灯图像、Conv1的输出特征图以及Conv2的输出特征图。

1) 卷积层，Conv

假设我们有N个输入车头灯训练图像{Ti} N i=1 ，大小为m × m，并且假设在第s阶段的卷积滤波器尺寸（或块大小）为ks × ks。在第一阶段（或s= 1）即Conv1中，我们使用方形块大小k1×k1从第i个训练图像中提取所有重叠块，并通过减去各自的块均值对每个块进行归一化。所有块被向量化并组合成矩阵形式

$$
X_i=[x_1^i, x_2^i,…, x_{\hat{m}\hat{m}}^i] \in R^{k_s \times k_s}
$$

其中，每个$x_j^i$表示 i中第j个向量化且归一化的图像块，而$\hat{m}= m −(k_s/2)$。均值归一化和向量化操作在所有输入的前大灯图像上进行，我们得到

$$
X=[X_1, X_2,…, X_N] \in R^{k_s k_s \times N \hat{m} \hat{m}}
$$

其中Xi是图像Ti的去均值向量。

然后我们计算VVT的特征向量。假设第s层的卷积滤波器数量为Fs。主成分分析用于在执行矩阵变换时最小化重构误差，其公式如下

$$
\min_{V\in R^{k_1\times k_2\times F_s}} | X - V V^T X | F^2, \quad \text{s.t. } V^T V= I {F_s}
$$

其中$IFS$是方阵大小为$Fs$的单位矩阵，$V=[V_1,V_2,…,V_m]$是$m × m$正交归一化滤波器。因此，将$XX^T$的$Fs$个主特征向量选作卷积阶段的PCA滤波器

$$
W_{sf} = \text{mat}_{k_s,k_s}(q_f(X X^T)) \in R^{k_s\times k_s}, \quad f= 1, 2,…, F_s
$$

其中，$\text{mat}_{k_s,k_s}(v)$ 是将向量形式的$v \in R^{k_s k_s}$ 转换为方阵权重矩阵$W \in R^{k_s\times k_s}$的操作，而$q_f(X X^T)$表示$XX^T$的第$f$个主特征向量。因此，我们提取$XX^T$的前$Fs$个主特征向量作为第$s-$阶段的卷积滤波器。这些提取出的主特征向量捕捉了去均值训练图像整体的主要方差，从而获得最大解释性。

在卷积阶段，利用主成分分析生成的权重滤波器，在第$s$阶段生成多个输出的卷积特征图，定义为$C_{sy}, y= 1, 2,…,N × Fs$，其中$y$为输出特征图总数。卷积过程的公式如下：

$$
C_{sy}= R(T_i \otimes W_{sf})
$$

其中⊗表示二维卷积操作，Ti是第i个输入图像或特征图，$W_{sf}$对应于在第s阶段由主成分分析（PCA）生成的第f个卷积滤波器，R是修正线性单元（ReLU），其计算方式为$R(x)= \max(0, x)$。与传统的常见激活函数如tanh或sigmoid相比，修正线性单元（ReLU）激活函数在特征提取过程中提供了非线性，对训练目的更有效[26]。

Conv2和Conv3层中的卷积阶段与Conv1类似，仅在卷积滤波器的尺寸和数量上有所不同。

2) 池化层1，Pool1

池化过程旨在显著缩小尺寸输入特征图，从而最大化输出对平移和旋转的不变性。更重要的是，此阶段还将减少参数数量，从而防止过拟合，并提高网络中的计算效率。每个输出特征图是在（s+1）‐th阶段通过对第s阶段前一层的相应特征图执行最大池化过程获得的

$$
C_{s+1 y} = \text{down}(C_{s y})
$$

其中$\text{down}(·)$是一个对输入特征图进行下采样的池化过程。我们采用尺寸为(px × py)的非重叠矩形区域，在前一层的输入特征图上检测并选取最大响应，其中下采样因子为px= py= 2，步长为=1。因此，该层输出特征图的尺寸将变为输入特征图尺寸的一半，即m/2和m/2。最终，车辆前照灯图像的多尺度特征将在该过程结束时被聚合。池化层2中的池化阶段将重复池化层1中的相同过程。

3) 全连接层，FC

线性分类在全连接层的末端实现。我们在网络的最后一层使用了softmax分类器（或多项逻辑斯蒂分类器）来对多类车头灯或车辆型号进行分类。来自前一个第三卷积层的具有固定维度的特征向量将作为输入馈送到softmax分类器。softmax分类器的输出产生每个前大灯图像对应其车辆型号类别的概率，其中概率最高的类别即为预测的车辆型号类别。为了生成多类车辆型号分类问题的输出概率，softmax分类器的响应变量h可取R个值，可以推广为

$$
P(h= r|x; W_L)= \frac{\exp(w_r^T x)}{\sum_{i=1}^R \exp(w_i^T x)}
$$

其中h是车辆型号类别标签，$x \in \mathbb{R}^{(K+1)\times 1}$是K维特征向量，$w \in \mathbb{R}^{(K+1)\times 1}$表示权重向量，$W_L=[w_1, w_2,…, w_N] \in \mathbb{R}^{(K+1)\times N}$为全连接层中的权重参数，每个wi对应不同类别的权重参数。

4) 交叉熵损失函数

为了衡量softmax层输出的预测类别与真实类别之间的误差，我们使用损失函数E(W)作为

$$
E(W)= -\left[\sum_{i=1}^N \sum_{r=1}^R 1{h^{(i)}= r}\log \frac{\exp(w_r^T x^{(i)})}{\sum_{j=1}^R \exp(w_j^T x^{(i)})}\right]
$$

其中$1{•}$表示指示函数，使得$1{$为真实类别$}= 1$或$1{$为虚假类别$}= 0$。为了防止过拟合问题，我们在公式(8)中添加了一个正则化项（或权重衰减项）D，其表达式为，

$$
D= \frac{\lambda}{2}\sum(W_L)^2
$$

其中WL是全连接层的权重参数，λ是权重衰减参数，我们在实验中使用λ= 10−5。

C. 反向传播与优化技术

我们利用反向传播（BP）通过仅更新全连接层的权重参数$W_L$及其偏置$B_L$来最小化误差或损失函数。通过网络向后传播的误差或增量可表示为每个单元或节点相对于全连接层参数扰动的敏感度。其表达式为

$$
\nabla_{W_L} E(W)= -\sum_{i=1}^N 1{h^{(i)}= r}- P(h^{(i)}= r|x^{(i)}; W_L)
$$

其中 $\nabla_{W_L}E(W)$表示全连接层权重参数$W_L$的梯度。采用随机梯度下降（SGD）优化技术在每次迭代中更新全连接层的权重参数。所有权重和偏置均基于LeCun et al.[27]提出的归一化初始化方法进行随机初始化，即$U[-(\sqrt{6}/\sqrt{n_i+ n_{i+1}}), (\sqrt{6}/\sqrt{n_i+ n_{i+1}})]$，其中$n_i$和$n_{i+1}$分别为第$i$层和第$i+1$层的神经元数量。反向传播计算梯度，而随机梯度下降使用小批量训练图像来更新权重参数。每次迭代中的新更新由以下公式给出：

$$
W_L^{i+1}= W_L^i - \alpha\nabla_{W_L} E(W)
$$

其中 $\alpha$是学习率。权重参数的更新通过使用代价及其相对于小批量大小的训练集的梯度来计算。在我们的方法中，初始值采用 $\alpha= 0.01$，并且每次SGD迭代的小批量大小为256张图像。在SGD中使用小批量可以最小化参数更新中的方差，从而在训练过程中实现更稳定的收敛。为了进一步加快收敛速度并避免在SGD训练过程中陷入局部极小值的问题，我们在模型中引入了动量方法。将更新向量的动量分数 $\gamma$融入当前的SGD更新中，从而得到公式(11)

$$
v^{i+1}= \gamma v^i+ \alpha_i\nabla_{W_L} E(W)^i
$$

其中$\alpha$表示第$i$次迭代时的学习率，$\gamma$设为0.9。权重和偏置参数的新更新定义如下

$$
W_L^{i+1}= W_L^i - v^{i+1}
$$
and
$$
b_L^{i+1}= b_L^i - v^{i+1}
$$

分别为，其中$v^i$表示与权重参数$W_L$具有相同维度的第$i$次迭代的速度向量，$\nabla_{W_L}E(W)^i$是在第$i$次迭代时关于$W_L$计算的损失函数的导数或梯度。学习率$\alpha_{i+1}$在每次迭代中进行退火处理。

$$
\alpha_{i+1}= \alpha_i \cdot (1+ 0.0005\cdot t)^{-1}
$$

其中$\alpha_i$是第$i$次迭代时的学习率。在结合上述所有步骤后，我们得到了经过优化的参数，这些参数由PCNN算法更新并获取，如算法1中所规定。

传统CNN的训练过程由于通过反向传播训练进行参数更新，所需时间呈指数增长。大量研究工作已经由[23],[24],和[28]开展，用于研究使用PCANet进行图像分类的有效性。因此，在我们的实验中，仅采用了PCANet在卷积阶段生成滤波器的策略。为了利用CNN的判别性拓扑并同时加快训练过程，我们对全连接层的权重参数进行初始化，然后迭代更新其参数。我们对测试数据集进行了验证

算法 1 基于PCANet的卷积神经网络（PCNN）

函数 PCNN $(T, W_{conv}, W_L, b_L, \alpha, \gamma)$
使用主成分分析生成$W_{conv}$
随机初始化 $W_L$ 和 $b_L$
重复在函数$(8)$中计算$E(W)$
在函数$(10)$中计算$\nabla_{W_L}E(W)$
使用随机梯度下降（SGD）在函数$(13)$中更新$W_L$
使用随机梯度下降在函数$(14)$中更新$b_L$
直到函数$(8)$被最小化
直到达到总迭代次数
返回$(W_L, b_L)$
结束函数

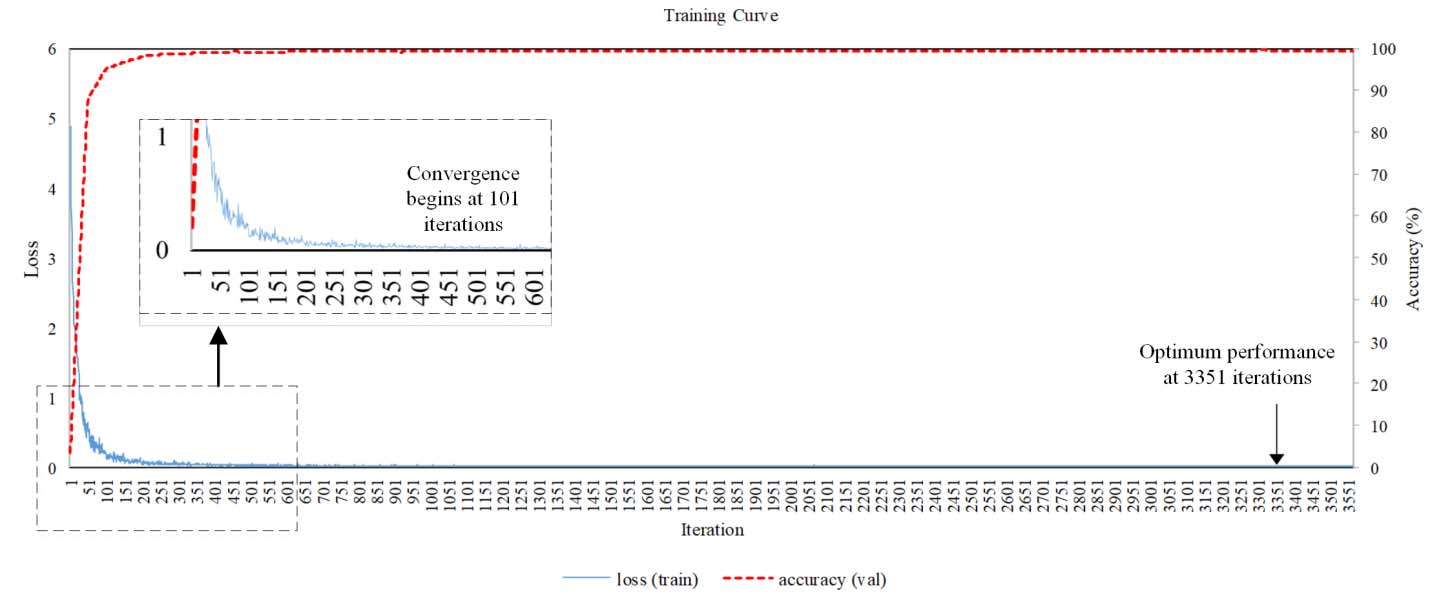
为了寻找更新后具有最佳分类性能的网络，每个训练周期都会进行迭代。如图4所示，该网络的训练过程在第101次迭代时开始收敛。事实上，如图4所示，我们的模型仅需36分钟即可完成PCNN的训练，并在第3351次迭代时达到最高的识别准确率。所有实验均在一台配备Intel Core i5中央处理器和8GB随机存取内存的台式机上，使用MATLAB 2015完成，未使用图形处理单元（GPU）。

III. 实验

A. 数据集

我们基于从PLUS马来西亚南北大道（NSE）生成的数据集评估了所提出模型的有效性和鲁棒性。该数据集包含了来自马来西亚最新的38种最常见的车型的车辆前大灯图像。总共采集了15960张户外车辆图像，这些图像是从电子道路收费系统的监控摄像头获取的。如图3所示，图像中包含了一些有用的车辆信息，例如车辆车牌、车辆品牌标志和前大灯细节。在我们提出的系统中，通过左前侧车头灯确定其独特特征，用于车辆型号分类。采集图像中的汽车根据左前侧前大灯被分为38种汽车型号。

所提出的系统已采用粗分割技术来定位和检测感兴趣区域（ROI），即前大灯区域。为此，首先使用滑动同心窗（SCW）方法检测车辆的车牌。以车牌作为参考点，随后定位并分割出左前侧大灯区域。车辆前照灯图像被转换为 100×100像素的灰度格式，并进行归一化处理。相机捕捉的原始图像表现出多种户外成像条件，例如光照变化。为了验证所提出系统的鲁棒性，我们进一步通过在图像中引入各种失真（如平移、旋转和噪声）来扩充数据集。一个包含13300张车辆前照灯图像的训练数据集和一个包含2660张车辆前大灯图像的测试数据集生成了38个车辆型号类别。这38个类别包含11个不同且在道路上常见的汽车品牌（或制造商）。一些相似的车辆型号因发布年份不同而被视为不同的类别，例如2013年发布的日产Almera，如图6(a)所示，及其2015年发布的改款车型，如图6(b)所示。

本研究共收集了38个车辆型号类别用于性能评估，分别为：Ford Fiesta、Nissan Almera N17、Nissan Almera N17 Facelift、Nissan Livina L10、Nissan Sylphy G11、Peugeot 207、Volkswagen Jetta、Volkswagen Polo、Suzuki Swift Second Generation、Suzuki Swift Third Generation、Honda Accord Eight Generation、Honda City Fourth Generation、Honda City Fifth Generation、Honda City Sixth Generation、Honda Civic FD、Honda Civic FB4、Honda Jazz Third Generation、Toyota Altis E140、Toyota Avanza F600、Toyota Camry XV40、Toyota Vios NCP42、Toyota Vios NCP93、Toyota Vios NCP150、Proton Exora、Proton Iriz、Proton Persona CM6、Proton Preve P3-21A、宝腾Saga BLM、宝腾Saga FLX、Perodua Alza、Perodua Axia、Perodua Bezza、Perodua Myvi第一代、Perodua Myvi第二代、Perodua Myvi第三代、Perodua Viva、现代伊兰特MD和起亚K3，如表I所示。

B. 结果与分析

提出了一种基于PCANet的卷积神经网络（PCNN）来评估车辆型号识别系统的性能。在所提系统中，我们通过多次实验选择了卷积核的数量和尺寸以实现最优性能。获得的车辆型号分类准确率基于从车辆图像中100%正确分割的车头灯区域。根据表I，车辆型号识别的平均准确率为99.51%。我们所提出的方法在利用车头灯作为感兴趣区域（ROI）的左前侧视角下表现良好。仅有总共13张识别错误的图像，这些图像属于以下类别：本田飞度、丰田Avanza、丰田Yaris NCP42、丰田Yaris NCP150、宝腾Exora、宝腾Preve、宝腾Saga FLX、Perodua Myvi第一代和Perodua Myvi第二代。与最近相关研究工作的比较结果列于表II中。即使仅使用一个特征或感兴趣区域（车头灯），我们所提模型在识别车辆型号方面仍优于其他已报道的方法。我们系统的训练过程和测试过程分别为36分钟和每张图像123毫秒。因此，我们所提方法的计算成本低，非常适合实时应用。这种低计算成本主要归因于采用了粗分割的车辆前大灯，因为车头灯具有足够的判别性来代表不同的车辆型号。此外，利用车头灯作为局部特征的优势在于系统只需计算少量参数，而无需提取其他最具判别性的特征，从而进一步降低了计算成本。

C. 讨论

为了验证所提模型的鲁棒性，我们进一步在1330张测试图像中引入了一些失真，即平移、旋转、噪声和光照。这些失真图像的质量比实时公共交通中的图像更差。每次实验的失真程度从低到高，包括极端情况。

1) 对平移的鲁棒性

我们进一步平移了粗分割车灯图像，如图7所示。

测试数据集有一半在水平方向或垂直方向，或两个方向上进行了平移。如表III所示，在平移5像素以内的识别准确率保持在90%以上。当平移超过10像素时，准确率开始显著下降。除平移为10像素的情况外，所有其他情况的准确率均高于70%。

在水平和垂直方向上均如此。如图7(c)所示，10像素的平移可能导致车头灯丢失重要的边缘信息。由于边缘是每个车辆型号类别独有的特征，丢失其中一部分将影响分类性能。因此，可以看出，包含完整形状或前大灯图像边缘的图像具有更好的性能。

2) 对缩放的鲁棒性

与之前的实验类似，从测试数据集中随机选择了1330张车头灯图像。在此实验中，对随机选择的测试图像应用了0.6到1.4范围内的不同缩放因子。图9展示了一些缩放后的前大灯图像示例。图8绘制了不同缩放因子下的平均准确率曲线。当缩放因子低于0.7或高于1.4时，分类准确率显著下降。可以看出，所提出的方法对缩放具有较强的鲁棒性，在缩放因子介于0.8和1.3之间时，其准确率保持在80%以上。

0.6、(b) 0.8、(c) 1、(d) 1.2、(e) 1.4的前大灯图像)

3) 对旋转的鲁棒性

在对车头灯进行粗略分割后，来自38个车辆型号类别的1330张测试图像被旋转 −20°至20°，如图11所示。旋转角度模拟了交通监控摄像头中的大多数极端情况。每张测试图像的平均识别准确率如图10所示。所提模型在 −15°至15°的旋转角度范围内实现了超过81%的准确率。

当旋转角度超过 ±15°时，准确率显著下降。可以看出，所提模型在 −15°到15°范围内的各种旋转角度下均具有较强的鲁棒性。

−20°, (b) −10°, (c) 0°, (d) 10°, (e) 20° 的前大灯图像)

4) 抗噪鲁棒性

由于各种成像条件的影响，从测试数据集中随机选择了1330张测试图像，并引入高斯噪声。为了验证所提模型的抗噪鲁棒性，在前大灯图像中引入了不同水平的高斯噪声。我们采用张等人的方法[31]，在随机选择的图像中引入噪声水平σ为10至100的高斯噪声。当噪声水平从10增加到100时，分类准确率略有下降。如图12所示，在所有噪声水平下，平均准确率均保持在97%以上。图13展示了受高斯噪声影响而质量下降的前大灯图像示例。其中一些图像因噪声干扰严重而几乎无法被观察者识别，如图13(e)所示。

20, (b) 40, (c) 60, (d) 80, (e) 100 的前大灯图像示例)

5) 特殊情况考虑

为了进一步验证系统在不同光照条件下的泛化能力，本文还研究了一些车头灯处于工作模式的车辆头灯图像，如图14(a)和(b)所示。这些图像是在低光条件下由交通监控摄像头拍摄的。我们使用所提模型对这些图像进行了测试，未进行任何额外的预处理过程或光照转换。尽管车头灯处于工作模式，我们所提的模型仍能基于前大灯图像识别车辆型号。异常情况明确列在错误分类一栏中。

表IV中的结果显示，前大灯与原始外观略有不同。因此，我们推测这些前大灯可能经过车主自行改装或定制化。由于我们的模型所学习到的最重要特征是前大灯结构和边缘，该结果表明，前大灯的物理改装会对识别结果产生一定影响。

6) 结果对比

我们还将MatConvNet[32]的CNN方法应用于我们的数据集。如表V所示，所提出的PCNN方法以99.51%的准确率优于CNN方法的98.68%。值得注意的是，所提出的PCNN的准确率是在未在GPU上并行实现的情况下达到的，而CNN运行则相反。显然，PCNN同时减少了计算时间并提高了分类准确率。

为了验证我们所提出方法的有效性，我们在车辆监控‐natureCom‐pCars数据集[18]上实现了PCNN。需要注意的是，在CompCars数据集中，无论发布年份如何，同一汽车型号都被归为同一个类别。事实上，同一型号但不同年份发布的车辆其车头灯可能具有不同的物理结构和特征。换句话说，同一个型号类别可能包含不止一种车头灯设计。此外，我们所提出的基于车头灯分类的识别方法对车头灯特征较为敏感。因此，我们根据车辆品牌、型号及其发布年份，将初始的车辆型号类别从281类进一步细分为357类。

Fang et al.[20]在CompCars数据集上实现了Zhang[15]和Hsieh et al.[12]的方法，结果如表VI所示。与其他最先进的方法相比，我们提出的方法在357个车辆型号上达到了89.83%的准确率。该方法不仅处理了最多的类别数量，而且取得了令人满意的结果。更重要的是，这带来了本工作的另一项重要成就，即它不仅能分类车辆品牌和型号（或车型间差异），还能基于车头灯特征进一步区分其发布年份的细微差异（或车型内变化）。据我们所知，目前尚无其他文献工作对此进行过如此深入的分析。

IV. 结论

本文提出了一种基于PCANet的卷积神经网络（PCNN）用于车辆型号识别。我们所提出的方法无需对车辆图像中的局部特征进行精确检测与分割。通过分层PCNN网络自动提取的判别性特征，对各种平移、旋转和噪声具有良好的鲁棒性。利用主成分分析（PCA）生成卷积滤波器，并仅使用一个重要的局部特征——车头灯，显著降低了训练过程的计算成本，同时取得了优异的结果。我们提出的系统在实时交通监控数据集上进行了实验，该数据集包含了马来西亚最新且最常见的车辆型号。为了验证所提系统的鲁棒性，测试数据集进一步引入了多种失真，即平移、旋转和噪声。此外，我们的系统还在全面的CompCars数据集上进行了评估，并取得了优异的结果。此外，结合GPU的并行实现将大大降低计算成本，使其更适用于实时应用。在未来工作中，我们将专注于更具挑战性的包含不同视角和失真的数据集。