在前面讨论的各种数据结构中,记录在各种结构中的相对位置是随机的,和在记录的关键字之间不存在有确定的关系,因此在查找记录是需要进行一系列和关键字的比较。
而理想的情况是不希望进行任何的比较,一次存取便能得到所查记录。那就必须在记录的存储位置和它的关键字之间建立一种确定的关系f,使每个关键字和结构中有一个唯一的存储位置与之相对应。我们称这个对应关系f为哈希函数,而按这个思想建立的表为哈希表。
许多应用都需要一种数据结构,支持查找,插入,删除的等字典操作。散列表(哈希表)是实现字典操作的一种有效的数据结构。尽管在最坏情况下,散列表中查找一个元素的时间与链表中查找的时间相同,达到了Θ(n)。但是实际应用中散列表的查找性能很好,平均时间可以达到O(1)。
散列表是普通数组概念的推广,在散列表中,不是直接把关键字作为数组的下标,而是根据关键字计算出相应的下标。散列是一种极其有效和实用的技术:基本的字典操作平均只需要O(1)的时间。
一:直接寻址表
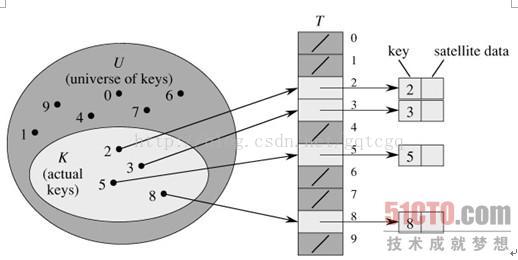
直接寻址表就是数组。当关键字的全域U比较小时,直接寻址是一种简单而有效的技术。比如,如果全域为U={0,1,…,m-1}。则可以使用长度为m的数组:
二:散列表
直接寻址技术的缺点很明显:如果全域U很大,则存储大小为|U|的数组是不切实际的,而且如果实际存储的关键字集合K相对于全域U来说很小的时候,会造成巨大的浪费。此时采用散列表。
1:定义
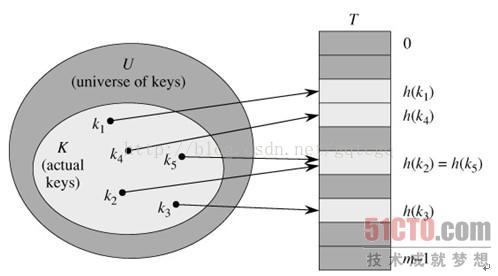
在直接寻址方式下,具有关键字k的元素存放在索引为k的位置中,在散列表中,该元素存放在h(k)中。h()就是一个散列函数。它将关键字的全域U映射到散列表T[0..M-1]的槽位上:
这里会存在所谓“冲突”的问题:两个关键字可能被映射到同一个槽位中。由于全域|U|>M,所以冲突是无法避免的,所以一方面需要精心设计散列函数来尽量减少冲突的次数,另一方面是需要解决冲突的方法。
2:链接法解决冲突
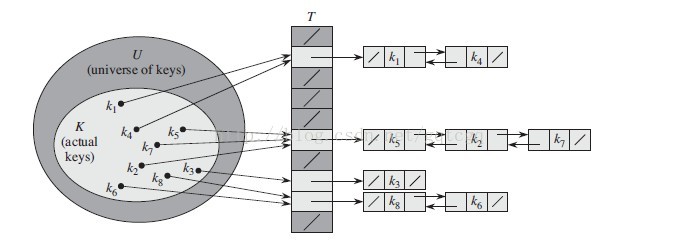
解决冲突的比较简单的方法就是链接法。它是把散列到同一个槽位的所有元素都放在一个链表中,然后数组中存放指针指向这个链表,如下图:
插入操作的最坏情况运行时间为O(1),因为只要计算出散列值,直接插入表头即可。
查找操作的最坏运行时间与表的长度成正比。
如果散列表中的链表是双向链表的话,删除一个元素可以在O(1)时间内完成。(以指针为参数,无须先查找)在单链表的情况下,删除和查找操作的运行时间相同。
3:链接法时间性能分析
给定一个具有m个槽位,存储了n个元素的散列表T,定义T的装载因子α为n/m,即,一个链表中的平均元素数目。α可能小于,等于,或大于1。
散列方法的平均性能依赖于所选取的散列函数h,将所有的关键字集合分布到m个槽位上的均匀程度。假定对于任何一个给定的元素,等可能的散列到m个槽位中的任何一个,且与其他元素被散列到什么位置上无关,称这个假设为简单均匀散列。
在简单均匀散列的情况下,对于采用链接法的散列表,一次不成功查找和一次成功查找所需的平均时间都为Θ(1+α)。因此,若散列表的槽位数正比于其中的元素个数,我们有n = O(m),于是,α = n/m = O(m)/m = O(1)。因此,查找时间平均为常数。由于插入操作首先需要调用CHAINED-HASH-SEARCH确认元素x的关键值未曾出现在表中,然后用O(1)时间将x插入到链表T[h(key[x])]中,所以期望的时间是O(1)。相仿地,删除操作对双向拉链表平均情形时间也是O(1),所以所有的字典操作可以在O(1)的平均时间内得到支持。
4:散列函数
一个好的散列函数应(近似的)满足简单均匀散列假设:每个关键字都等可能的被散列到m个槽位中的任何一个,并与其它关键字已散列到哪个槽位无关。遗憾的是一般无法检查这一条件是否成立,因为很少能知道关键字的概率分布,而且各个关键字可能不是完全独立的。
如果知道关键字的概率分布,比如关键字都是随机的k,它们独立均匀分布在区间[0…1]中,那么散列函数h(k) = km就能满足简单均匀散列的条件。
多数散列函数都假定关键字的全域为自然数集。因此如果给定的关键字不是自然数,需要找到一种方法将它们转换为自然数。比如一个字符串可以被转换为按适当的基数符号表示的整数。
a:除法散列法
散列函数为h(k) = k mod m
其中m为散列表的槽位数,使用除数散列法的时候,对于m的选择要慎重。比如m不应该是2的幂。否则如果m = 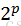
一个不太接近2的整数幂的素数是m个一个比较好的选择。
b:乘法散列法
h(k) = m(kA mod 1)
第一步,用关键字k乘以常数A(0<A<1),提取KA的小数部分(kA mod 1)。
第二部,用m乘以这个值。
在乘法散列法中,m的选择不是关键,一般选择m为2的某个次幂。最佳的选择为(A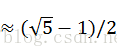
c:直接定址法
h(k) = k或 h(k) = a k + b 其中a和b为常数。实际中能使用这种哈希函数的情况很少。
数字分析法
假设关键字是以r为基的数(比如以10为基的十进制数),并且哈希表中可能出现的关键字都是事先知道的,则可取关键字的若干位组成哈希地址。
实际工作中需要根据不同的情况采用不同的哈希函数。通常,考虑的因素有:
计算哈希函数所需的时间;
关键字的长度;
哈希表的大小;
关键字的分布情况;
记录的查找频率。
5:开放寻址法
开放寻址法是另外一种处理冲突的方法。在该方法中,所有的元素都存放在散列表中。当查找某个元素的时候,需要系统的检查所有的表项,直到找到所需的元素,或者最终查明该元素不在表中。因此,在开放寻址法中,散列表有可能会被填满,因而装载因子α <= 1。
在开放寻址法中,字典操作需要找到一个”槽序列”,比如要插入元素,需要按照某个槽序列探查散列表,直到找到一个空槽。探查的序列不一定是0,1…m-1。而是要依赖于待插入的关键字。对于每一个关键字k,探查序列为:h(k,i) (0 <= i <= m-1)。伪代码如下:
HASH_INSERT(T, k)
i= 0
repeat
j = h(k, i);
if T[j] == NIL
T[j]= k;
return j;
else
i += 1;
until i==m
error "hash table overflow"
HASH_SERACH(T,k)
i = 0
repeat
j = h(k, i)
if T[j] == k
return j
i = i+1
until T[j] == NIL or i ==m
return NIL
删除操作执行起来比较困难,当我们从槽i中删除关键字时,不能简单地让T[i]=NIL,因为这样会破坏查找的过程。假设关键字k在i之后 插入到散列表中,如果T[i]被设为NIL,那么查找过程就再也找不到k了。解决这个问题的方法是引入一个新的状态DELETED,而不是NIL,这样在插入过程中,一旦发现DELETED的槽,便可以在该槽中放置数据,而查找过程不需要任何改动。但如此一来,查找时间就不再依赖于装载因子了,所以在必须删除关键字的应用中,往往采用链接法来解决碰撞。
均匀散列:假设每个关键字的探查序列等可能的为(0,1,……m-1)的m!种排列中的任何一种。真正的均匀散列难以实现,有三种技术常用来计算开放寻址法中的探查序列:线性探查,二次探查,双重探查。这些技术均不满足均匀散列的假设。
a:线性探查
h(k,i) = (h’(k) + i) mod m, i = 0,1,…,m-1
给定一个关键字k,首先探查槽位h’(k),然后是h’(k) + 1,以此类推,直到最后的h’(k)-1。在线性探查中,初始探查位置决定了整个序列,所以有m种不同的探查序列。
线性探查有个缺点,就是一次群集。当表中i,i+1,i+2位置上都已经填满时,下一个哈希地址为i,i+1,i+2,i+3的关键字记录都将竞争i+3的位置。随着连续被占用的槽位不断增加,平均查找时间也不断增加。
b:二次探查
h(k,i) = (h’(k) + 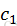
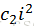
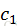
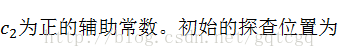
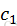
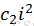
c:双重散列
h(k,i) = ( 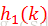
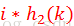
双重散列是开放寻址法中的最好方法之一,不像线性和二次探查,双重探查的的探查序列以两种不同的方式依赖于关键字k。为了能使探查序列查找到整个表,值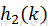
m为2的幂,而 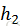
取m为素数, 则总是产生比m小的正整数。
双重探查法用到了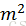
在开放寻址中,对于装载因子α,并假设是均匀散列,至多需要做1/(1-α)次探查。





















 2575
2575











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








