开头
背包问题
1.01 背包
01背包概述
01背包问题实质是组合问题,要求对于一堆信息,在有限制的条件下选择符合要求的方案
一般会用到两维,一维表示枚举到的物品,一维表示当前枚举的体积,用f[i][j]表示。
就最传统的01背包问题来说,集合划分依据,是当前枚举到的第i个物品选还是不选,对于不选,那么当前状态等价于f[i-1][j]
如果选,还需要细分为剩余体积是否能容下,如果能容下,当前状态等价于对于前i-1个物品去除当前物品的体积所能表示的集合,再加上当前物品的价值,
也就是f[i][j]=f[i-1][j-v[i]]+w[i];
可以发现在枚举物品时,状态的转移只和上一层状态相关,所以使用滚动数组优化,在使用滚动数组时,一定要注意,不能有状态的覆盖,例如经典01背包,如果体积还是从小到大枚举,那么当我们枚举到大体积时,会用到小体积的状态,但小体积的状态已经被覆盖,不再是上一层的状态,而是当前层的状态,所以01背包中的体积枚举要从大到小
代码模板
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1100;
int f[N];
int w[110],v[110];//w[]是物品体积,v[]是物品价值
int t;
int n;
int main()
{
cin>>t>>n;
for(int i=1;i<=n;i++)
{
cin>>w[i]>>v[i];
}
for(int i=1;i<=n;i++)
for(int j=t;j>=w[i];j--)
{
f[j]=max(f[j],f[j-w[i]]+v[i]);
}
cout<<f[t]<<endl;
}
1.采药
链接link
2.装箱问题
链接link
3.数字组合
链接link
4.波动数列
链接link
观察这个数列:
1 3 0 2 -1 1 -2 …
这个数列中后一项总是比前一项增加2或者减少3,且每一项都为整数。
栋栋对这种数列很好奇,他想知道长度为 n
和为 s
而且后一项总是比前一项增加 a
或者减少 b
的整数数列可能有多少种呢?
输入格式
共一行,包含四个整数 n,s,a,b
,含义如前面所述。
输出格式
共一行,包含一个整数,表示满足条件的方案数。
由于这个数很大,请输出方案数除以 100000007
的余数。
首先,在处理数学相关的题目时,应该先试着把公式写出来,由于这题是与数列相关,数列一般会有通项公式,所以先尝试把数列的通项公式写出来。
假设首项为x1,x1+x2+x3+…+xn=s,将x1,x2…xn替换成与x1相关的式子,x2=x1+d1,x3=x1+d1+d2,xn=x1+d1+d2+…+dn-1
所以可以变形为
nx1+(n-1)d1+(n-2)d2+…+2dn-2+dn-1=s
x1=[s-((n-1)d1+(n-2)d2+…+dn-1)]/n
根据题意可知,di为a或-b,这就转换成了,一共有n-1个数,每个数有两种选择,要将这n-1个选择组合在一起,求有多少种这样的方案。
在这题中的合法方案,就是组合后的x1是符合条件的数字,也就是x1为整数,所有对于[s-((n-1)d1+(n-2)d2+…+dn-1)]这部分来说,只有满足能整除n时,x1才会是整数,对于这种分子相减的形式,可以转换成同余形式,
s≡(n-1)d1+(n-2)d2+…+dn-1 (mod n)
分析到这步其实已经和x1无关了。
接来下定义状态表示:
首先,我们需要一维来枚举d,记为状态i,对于经典01背包的体积那维,在这道题中,应该是与余数相关的,怎么考虑这一维呢?
假设我们已经有了前n-1项,那对于第n项来说,怎么才能满足条件呢?
很显然,我们需要始终满足同余这个条件,第i项的通式为(n-i)di,
s≡c+(n-i)di,c≡s-(n-i)di
对于背包问题来说,是一个维数逐步扩大的枚举过程,例如经典背包中的体积,需要从小到大枚举所有符合的情况,
所以我们将s替换成需要枚举的j,所以第二维就定义成了总和%n =j;
所以f[i][j]:对于前i个数,总和对n取余的结果为j的所有方案的集合,集合属性为count
接下来考虑集合划分,我们将第di个取a,或-b作为划分依据
对于情况1,假设前面所有数的和为c
[c+(n-i)*a]%n=j;对于集合的划分,一定是从之前有的状态推得现有的状态,所以我们先考虑去掉第i项后前i-1项的情况是什么,
去掉第i项后,对等式变形,可得c ≡j-(n-i)*a mod(n),
f[i][j]=f[i-1][get_mod(j-(n-i)*a,n)]
对于情况2,同理可得
f[i-1][get_mod(j+(n-i)*b,n)]
由于集合是count,所以两种情况相加,就是这层的状态
对于取余数,要保证是正余数,有公式(a%b+b)%b
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1010,MOD=100000007;
int f[N][N];
int get_mod(int a,int b)
{
return (a%b+b)%b;
}
int main()
{
int n,s,a,b;
cin>>n>>s>>a>>b;
f[0][0]=1;
for(int i=1;i<n;i++)
for(int j=0;j<n;j++)
{
f[i][j]=(f[i-1][get_mod(j-(n-i)*a,n)]+f[i-1][get_mod(j+(n-i)*b,n)])%MOD;
}
cout<<f[n-1][get_mod(s,n)]<<endl;
}
2.完全背包
完全背包概述
完全背包与01背包最大的不同在于,每件物品不再是最多只能选1件,而是可以无限选
f[i][j]还是表示对于前i件物品,体积为j的所有满足方案的集合
考虑集合划分,以第i件物品选几件为划分依据
对于f[i][j]=max(f[i-1][j-0w[i]]+0v[i],f[i-1][j-1w[i]]+1v[i],f[i-1][j-2w[i]]+2v[i],f[i-1][j-kw[i]]+kv[i])
如果就这样枚举的话,我们需要枚举三维的变量,一维是物品数,二维是体积,三维是选择个数,很多情况下这样做会超时。
正如上文所提及,在做动态规划的问题时,都是从已知的状态去推断未知的状态,所以当i-1不好用时,就试着考虑下j-v[i]的情况,这样的推断也是满足要求的
f[i][j-v]=max(f[i-1][j-w]+f[i-1][j-2*w]+v+…+f[i-1][j-kw]+(k-1)v+f[i-1][j-kw]+(k-1)*v
这样就可以把f[i][j]中除了第一项外的式子等价替换成f[i][j-v]+v
这样的话f[i][j]=max(f[i-1][j],f[i-1][j-v]+v)
在完全背包中,当前状态的更新实际上用到的是本层的状态,所以不管怎么枚举体积,都不会改变上一层的状态,所以实际在写的时候,与01背包唯一的不同,就是枚举体积时,不需要从大到小枚举
代码模板
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1010;
int n,m;
int v[N],w[N];
int f[N];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
for(int j=v[i];j<=m;j++){
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
cout<<f[m]<<endl;
}
1. 买书
链接link
2.货币系统1
链接link
3.货币系统2
链接link
在网友的国度中共有 n种不同面额的货币,第 i 种货币的面额为 a[i],你可以假设每一种货币都有无穷多张。
为了方便,我们把货币种数为 n、面额数组为 a[1…n]的货币系统记作 (n,a)。
在一个完善的货币系统中,每一个非负整数的金额 x
都应该可以被表示出,即对每一个非负整数 x,都存在 n个非负整数 t[i] 满足 a[i]×t[i]的和为 x。
然而,在网友的国度中,货币系统可能是不完善的,即可能存在金额 x不能被该货币系统表示出。
例如在货币系统 n=3,a=[2,5,9]中,金额 1,3就无法被表示出来。
两个货币系统 (n,a)和 (m,b)
是等价的,当且仅当对于任意非负整数 x
,它要么均可以被两个货币系统表出,要么不能被其中任何一个表出。
现在网友们打算简化一下货币系统。
他们希望找到一个货币系统 (m,b)
,满足 (m,b)
与原来的货币系统 (n,a) 等价,且 m尽可能的小。
他们希望你来协助完成这个艰巨的任务:找到最小的 m。
本题的题意就是尽量减少原数组的元素个数,得到的新数组具有和原数组一样的功能,也就是对于任意一个x,要么同时能被凑出来,要么就同时不能被凑出来,
有个很直观的感觉,就是新数组里的数就是原数组里的数,并且是不能用里面的数凑出来的。对于这种贪心的思想,最好给出严格的证明.
假设存在a[],b[],两个数组满足题意,即size(b)<size(a),并且功能等价.假设b中存在某个元素不属于a,对于一个数x来说,可以被a,b凑出来
x=∑aiti,
x=bm*tm+c, bm是不属于a的一个数
首先c是能被b[]凑出来的数,根据条件,也是能被a[]凑出来的数可以把c也写成∑aiti,把t替换成k,c=∑aiki,
x-c>=0&&x-c=∑ai*(ti-ki),所以bmtm一定是可以被a[]凑出来的,
bmtm能被凑出来的前提条件是bm能被凑出来,所以bm一定能被a[]凑出来,同时,根据题意,bm一定不会是多个ai拼凑出来的,这个证明先留着,所以bm只能是a[]中的某个数,这就与假设矛盾,所以一定不存在某个bi,不属于ai
贪心2:最优数组b[]中的元素一定不会是多个ai拼凑而来的
假设最优解中存在某个元素是由多个ai拼凑出来的,已知有个数组b1[],这其中除了那个有多个ai拼凑出来的元素,其他元素与最优解相同,那么是否有元素是b[]能凑出,但b1[]不能凑出的呢,很显然不存在
所以本题就转换成了完全背包问题,首先要对原数组排序,对于第i个元素,考虑能否被前i-1个元素凑出
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=110,M=25100;
int t;
int n;
int a[N];
bool f[M];
int main()
{
cin>>t;
while(t--)
{
cin>>n;
memset(f,false,sizeof f);
for(int i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+1+n);
int res=0;
f[0]=true;
for(int i=1;i<=n;i++)
{
if(!f[a[i]]) res++;
for(int j=a[i];j<=a[n];j++)
f[j]|=f[j-a[i]];
}
cout<<res<<endl;
}
}
4.整数划分
链接link
5.包子凑数
链接link
小明几乎每天早晨都会在一家包子铺吃早餐。
他发现这家包子铺有 N
种蒸笼,其中第 i
种蒸笼恰好能放 Ai
个包子。
每种蒸笼都有非常多笼,可以认为是无限笼。
每当有顾客想买 X
个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干笼中恰好一共有 X
个包子。
比如一共有 3
种蒸笼,分别能放 3、4
和 5
个包子。
当顾客想买 11
个包子时,大叔就会选 2
笼 3
个的再加 1
笼 5
个的(也可能选出 1
笼 3
个的再加 2
笼 4
个的)。
当然有时包子大叔无论如何也凑不出顾客想买的数量。
比如一共有 3
种蒸笼,分别能放 4、5
和 6
个包子。
而顾客想买 7
个包子时,大叔就凑不出来了。
小明想知道一共有多少种数目是包子大叔凑不出来的。
输入格式
第一行包含一个整数 N。
接下来 N
行,每行包含一个整数 Ai。
输出格式
输出一个整数代表答案。
如果凑不出的数目有无限多个,输出INF。
数据范围1≤N≤100,1≤Ai≤100
输入样例1:
2
4
5
输出样例1:
6
输入样例2:
2
4
6
输出样例2:
INF
样例解释
对于样例1,凑不出的数目包括:1, 2, 3, 6, 7, 11。
对于样例2,所有奇数都凑不出来,所以有无限多个。
对于不能被凑出来的数,有一结论,只要用来凑数的几个数的最大公约数为1,那么就一定不会有无穷项凑不出来,相反,如果最大公约数不为1,那么就有无限项凑不出来.
可以简单证明下,首先,用来凑数的数都可以用他们的最大公约数的倍数来表示,ai=gcdti,所以说,用这几个数凑出来的数也满足公式x=gcdti,也就是说x一定是gcd的倍数,那么不是gcd倍数的数就一定没法凑出来,任何数都是1的倍数,所以,gcd=1时,就不会有无限个数凑不出来
这题首先的思路,就是先判断给出的数组是否最大公约数为1,接下来就是按照完全背包的思路来做
在凑数问题中,集合的属性应该是bool,也就是说数组记录的应该是一个数能否被凑出来,但本题需要不能被凑出来的数量,所以还需要一个变量来记录.
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=10010;
int a[110];
bool f[110][N];
int res;
int gcd(int a,int b)
{
return b?gcd(b,a%b):a;
}
int main()
{
int n;
scanf("%d",&n);
int d=0;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
d=gcd(d,a[i]);
}
if(d!=1)puts("INF");
else
{
f[0][0]=true;
for(int i=1;i<=n;i++)
for(int j=0;j<N;j++)
{
f[i][j]=f[i-1][j];
if(j>=a[i])f[i][j]|=f[i][j-a[i]];//只要有一种方案符合就行
}
int res=0;
for(int i=0;i<N;i++)
{
if(!f[n][i]) res++;
}
printf("%d",res);
}
}
3.多重背包
多重背包概述
多重背包中每个物品的选择次数不再是无上限,而是规定一定的数量
1.朴素版做法
在枚举物品和体积时,多一维枚举物品的数量
朴素版代码模板
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=25000;
int f[N];
int n,m;
int main()
{
cin>>n>>m;
f[0]=0;
for(int i=1;i<=n;i++)
{
int v,w,s;
cin>>v>>w>>s;
for(int j=m;j>=0;j--)
for(int k=0;k*v<=j&&k<=s;k++)
{
f[j]=max(f[j],f[j-k*v]+k*w);
}
}
cout<<f[m]<<endl;
}
2.二进制优化版:
可以思考,在枚举物品数时候,是否需要逐个枚举物品数呢,其实不需要,因为物品数量这一性质是具有结合律的,比如要拿三件物品,先拿两件,再拿一件也是可以的,既然如此,就可以使用倍增思想,类似于快速幂,所以二进制优化的多重背包的关键就在于,预处理物品数量,将其1种物品,按照取的数量,打包成多份体积和价值不同的商品,然后用01背包来解决
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
const int N=25000;
vector<int>v;
vector<int>w;
int f[N];
int n,m;
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
int a,b,s;
cin>>a>>b>>s;
int k=1;
while(k<=s)
{
v.push_back(k*a);
w.push_back(k*b);
s-=k;
k*=2;
}
if(s>0)
{
v.push_back(s*a);
w.push_back(s*b);
}
}
for(int i=0;i<v.size();i++)
for(int j=m;j>=v[i];j--)
f[j]=max(f[j],f[j-v[i]]+w[i]);
cout<<f[m]<<endl;
}
3.滑动窗口优化
4.分组背包
分组背包概述:
每组物品有若干个,同一组内的物品最多只能选一个,由此可以发现,对于同一组而言,必定只能选择一个,因为两两是互斥的。所以
考虑是否使用分组背包时,要抓住分组背包的实质是组内互斥
1.机器分配
总公司拥有M台 相同 的高效设备,准备分给下属的N个分公司。
各分公司若获得这些设备,可以为国家提供一定的盈利。盈利与分配的设备数量有关。
问:如何分配这M台设备才能使国家得到的盈利最大?
求出最大盈利值。
分配原则:每个公司有权获得任意数目的设备,但总台数不超过设备数M。
输入格式
第一行有两个数,第一个数是分公司数N,第二个数是设备台数M;
接下来是一个N*M的矩阵,矩阵中的第 i 行第 j 列的整数表示第 i 个公司分配 j 台机器时的盈利。
输出格式
第一行输出最大盈利值;
接下N行,每行有2个数,即分公司编号和该分公司获得设备台数。
答案不唯一,输出任意合法方案即可。
数据范围
1≤N≤10
,
1≤M≤15
输入样例:
3 3
30 40 50
20 30 50
20 25 30
输出样例:
70
1 1
2 1
3 1
根据题意,每个分公司提供的赢利一定是唯一的,也就是说,对于不同的分配方案,效果是互斥的,所以可以用分组背包解决,将同一个分公司的不同分配方案,看做一个物品组。
题目还有一个难点,就是如何求具体方案,对于dp求具体方案,一般用图论的方法思考,如果将dp看做一个最短路问题,那么具体的方案,就是点与点之间的转移,所以可以从后往前倒推出具体方案,
同时存入一个答案数组中
#include<iostream>
#include<algorithm>
using namespace std;
const int N=20;
int f[N][N];
int w[N][N];
int n,m;
int path[N];
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
cin>>w[i][j];
}
for(int i=1;i<=n;i++)//枚举物品
for(int j=0;j<=m;j++)//枚举体积
for(int k=0;k<=m;k++)//枚举选几次
{
if(j>=k)
{
f[i][j]=max(f[i][j],f[i-1][j-k]+w[i][k]);
}
}
cout<<f[n][m]<<endl;
//倒推方案,从后往前得到方案路径
int j=m;//先将体积变为最大,方便倒推
for(int i=n;i>=1;i--)
for(int k=0;k<=j;k++)//与01背包不同,还需枚举选择次数
{
if(f[i][j]==f[i-1][j-k]+w[i][k])
{
path[i]=k;
j-=k;
break;//只要找到一种方案就行
}
}
for(int i=1;i<=n;i++) cout<<i<<" "<<path[i]<<endl;
}
2.金明的预算方案
link
这题也可归为有依赖的背包问题。根据题意,首先将所有物品化作两类,一类为主件,一类为附件,同时组内的选择方案是互斥的,所以可以考虑分组背包解决,由于组内还需要枚举所有方案数,
但附件的数量并不大,所以还可以采用二进制优化的方式,枚举所有选择方案
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
#define v first
#define w second
using namespace std;
typedef pair<int, int> PII;
const int N = 60, M = 32010;
int n, m;
PII master[N];
vector<PII> servent[N];
int f[M];
int main()
{
cin >> m >> n;
for (int i = 1; i <= n; i ++ )
{
int v, p, q;
cin >> v >> p >> q;
p *= v;
if (!q) master[i] = {v, p};
else servent[q].push_back({v, p});
}
for (int i = 1; i <= n; i ++ )
for (int u = m; u >= 0; u -- )
{
for (int j = 0; j < 1 << servent[i].size(); j ++ )
{
int v = master[i].v, w = master[i].w;
for (int k = 0; k < servent[i].size(); k ++ )
if (j >> k & 1)
{
v += servent[i][k].v;
w += servent[i][k].w;
}
if (u >= v) f[u] = max(f[u], f[u - v] + w);
}
}
cout << f[m] << endl;
return 0;
}
5.二维费用的背包
概述:
思考方式与普通的背包问题并无多大区别,只需要多开几维即可
link
/*
集合:所有只从前i个物品中选,且总体积不超过j,总重量不超过k的选法
状态表示f[i,j,k]
属性:Max
状态计算 集合划分:1.所有不包含物品i的选法 2.所有包含物品i的选法
*/
#include<iostream>
using namespace std;
const int N=110;
int n,V,M;
int f[N][N];
int main()
{
cin>>n>>V>>M;
for(int i=0;i<n;i++)
{
int v,m,w;
cin>>v>>m>>w;
for(int j=V;j>=v;j--)
for(int k=M;k>=m;k--)
f[j][k]=max(f[j][k],f[j-v][k-m]+w);
}
cout<<f[V][M]<<endl;
}
潜水员
/*
集合:所有从前i个物品中选,且氧气含量至少是j,氮气含量至少是k的所有选法
状态表示f[i,j,k]
属性:Min
状态计算 1.所有不含物品i的所有选法 2.包含物品i的所有选法
体积描述的区别:
1.体积最多是j,初始化是全部是0,对于f(0,i),如果一件物品不选,不管体积多大价值都为0
2.体积恰好是j,初始化时,f(0,0)=0,其他为无穷(无穷根据题目是求最大值还是最小值确定),
对于f(0,i),只有i为0时才有可能存在,其他情况下不管怎么取都不存在
3.体积至少是j,初始化时,f(0,0)=0,其他为无穷,但在转移是f(0,负数)是合法状态,因为这个意思是至少为一个负数,
对于任何一个正数,都满足至少是负数的条件,所以遇到这种情况等价于f(x,0)
*/
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=22,M=80;
int n,m,k;
int f[N][M];
int main()
{
cin>>n>>m>>k;
memset(f,0x3f,sizeof f);
f[0][0]=0;
while(k--)
{
int v1,v2,w;
cin>>v1>>v2>>w;
for(int j=n;j>=0;j--)
for(int k=m;k>=0;k--)
f[j][k]=min(f[j][k],f[max(0,j-v1)][max(0,k-v2)]+w);
}
cout<<f[n][m]<<endl;
}
6.背包问题对于体积描述的区别
体积描述的区别:
1.体积最多是j,初始化是全部是0,对于f(0,i),如果一件物品不选,不管体积多大价值都为0
2.体积恰好是j,初始化时,f(0,0)=0,其他为无穷(无穷根据题目是求最大值还是最小值确定),
对于f(0,i),只有i为0时才有可能存在,其他情况下不管怎么取都不存在
3.体积至少是j,初始化时,f(0,0)=0,其他为无穷,但在转移是f(0,负数)是合法状态,因为这个意思是至少为一个负数,
对于任何一个正数,都满足至少是负数的条件,所以遇到这种情况等价于f(x,0)# 7.混合背包
8.有依赖的背包问题
有 N
个物品和一个容量是 V
的背包。
物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。
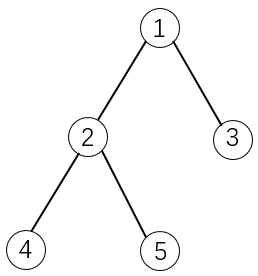
如下图所示:
如果选择物品5,则必须选择物品1和2。这是因为2是5的父节点,1是2的父节点。
每件物品的编号是 i
,体积是 vi
,价值是 wi
,依赖的父节点编号是 pi
。物品的下标范围是 1…N
。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
因为题目所给的是一个树形,所以考虑用树形dp来解决,可以发现,本题和金明的预算方案很像,最大的区别在于对于父节点来说,子节点的方案数可以有非常多,如果还用枚举方案的方法,作为集合的划分,效率非常低,所以需要新的集合划分依据,因为这题还用体积的限制,所以将体积作为集合的划分依据
/* 集合:所有从以u为根的子树中选,且总体积不超过j的方案
目标:f[u,j]
属性:Max
树形dp的框架,与金明的预算方案不同的地方是,金明的预算方案对于集合的划分依据是物品的选择,有2^k种,
但本题k有100,所以改变划分依据,根据体积来划分,这样会划分成m+1种,转变为多重背包问题
*/
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=110;
int n,m;
int v[N],w[N];
int h[N],e[N],ne[N],idx;
int f[N][N];
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u)
{
//对于物品u的何时放入有两种方式:1.是在遍历子节点的时候就加上,2.先去除物品u的体积,先考虑子节点的情况,再加上根节点
for(int j=v[u];j<=m;j++) f[u][j]=w[u];
for(int i=h[u];i!=-1;i=ne[i])
{
int son=e[i];
dfs(son);
for(int j=m;j>=v[u];j--)
{
for(int k=0;k<=j-v[u];k++)
f[u][j]=max(f[u][j],f[u][j-k]+f[son][k]);
}
}
//for(int i=m;i>=v[u];i--) f[u][i]=f[u][i-v[u]]+w[u];
//for(int i=0;i<v[u];i++) f[u][i]=0;
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof h);
int root;
for(int i=1;i<=n;i++)
{
int p;
cin>>v[i]>>w[i]>>p;
if(p==-1) root=i;
else add(p,i);
}
dfs(root);
cout<<f[root][m]<<endl;
}
9.背包问题求方案数
有 N
件物品和一个容量是 V
的背包。每件物品只能使用一次。
第 i
件物品的体积是 vi
,价值是 wi
。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出 最优选法的方案数。注意答案可能很大,请输出答案模 109+7
的结果。
动态规划可以理解为最短路问题,起点为(0,0) 终点为(n,m)
求最优解的数量,想到与最短路中求最短距离的条数
f[i,j]=max(f[i-1,j],f[i-1,j-vi]+wi)
g[i,j]表示f[i,j]取最大值的方案数
1.f[i-1,j]>f[i-1,j-vi]+wi g[i-1,j]
2.f[i-1,j]<f[i-1,j-vi]+wi g[i-1,j-vi]
3.f[i-1,j]=f[i-1,j-vi]+wi g[i-1,j]+g[i-1,j-vi]
#include<iostream>
#include<cstring>
using namespace std;
const int N=1010,mod=1e9+7;
int n,m;
int f[N],g[N];
int main()
{
cin>>n>>m;
//状态取恰好为j
memset(f,-0x3f,sizeof f);
f[0]=0;
g[0]=1;
for(int i=0;i<n;i++)
{
int v,w;
cin>>v>>w;
for(int j=m;j>=v;j--)
{
int maxv=max(f[j],f[j-v]+w);
int cnt=0;
if(maxv==f[j]) cnt+=g[j];
if(maxv==f[j-v]+w) cnt+=g[j-v];
g[j]=cnt%mod;
f[j]=maxv;
}
}
int res=0;
for(int i=0;i<=m;i++) res=max(res,f[i]);
int cnt=0;
for(int i=0;i<=m;i++)
if(res==f[i])
cnt=(cnt+g[i])%mod;
cout<<cnt<<endl;
}
10.背包问题求具体方案
有 N
件物品和一个容量是 V
的背包。每件物品只能使用一次。
第 i
件物品的体积是 vi
,价值是 wi
。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出 字典序最小的方案。这里的字典序是指:所选物品的编号所构成的序列。物品的编号范围是 1…N
如果只需要求出具体方案,那么可以像考虑最短路问题一样,用一个数组记录状态的转移即可,但题目还要求字典序最小,
如何求字典序最小的路径,可以从第一个物品开始思考,如果是能选就一定要选,不能选就一定不选
但路径是从终点开始倒推的,与求最小字典序的顺序是相反的,所以要想办法把这两顺序一致化,
可以将状态方程的计算顺序颠倒,这样就能将终点变为起点,在求最小字典序的过程中,还是从第一个物品开始枚举,
这样就能满足题意
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1010;
int f[N][N];
int v[N],w[N];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>v[i]>>w[i];
}
for(int i=n;i>=1;i--)//从最后一个物品开始枚举
for(int j=0;j<=m;j++)
{
f[i][j]=f[i+1][j];
if(j>=v[i])
{
f[i][j]=max(f[i+1][j],f[i+1][j-v[i]]+w[i]);
}
}
//结束后f[1][m]相当于正常的f[n][m],因为路径是从终点开始倒推的,所以下一次路径根据f[2][m-v]
//正常顺序 1<--2<--3...<---n-1<---n 交换后的顺序n<--n-1<---n-2...<---2<---1
int j=m;
int sum=0;
for(int i=1;i<=n;i++)
if(j>=v[i]&&f[i][j]==f[i+1][j-v[i]]+w[i])
{
cout<<i<<" ";
j-=v[i];
}
}





















 9412
9412











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








