相信大家考计算机二级时都背过这个关于二叉树的概念,不过只有自己动手写出来时才会发现它的奇妙之处。
先巩固一下概念:
二叉树的每个结点至多只有二棵子树(不存在度大于2的结点),二叉树的子树有左右之分,次序不能颠倒。二叉树的第i层至多有 个结点;深度为k的二叉树至多有
个结点;深度为k的二叉树至多有 个结点;对任何一棵二叉树T,如果其终端结点数为
个结点;对任何一棵二叉树T,如果其终端结点数为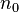 ,度为2的结点数为
,度为2的结点数为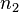 ,则
,则 。
。
 个结点;深度为k的二叉树至多有
个结点;深度为k的二叉树至多有 个结点;对任何一棵二叉树T,如果其终端结点数为
个结点;对任何一棵二叉树T,如果其终端结点数为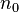 ,度为2的结点数为
,度为2的结点数为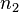 ,则
,则 。
。

1)二叉树数据结构
typedef struct node{
char data;
struct node *left;
struct node *right;
}BT;BT *creat_test()
{
/*
A
/ \
B C
/
D
\
E
*/
BT *pA=(BT *)malloc(sizeof(BT));
BT *pB=(BT *)malloc(sizeof(BT));
BT *pC=(BT *)malloc(sizeof(BT));
BT *pD=(BT *)malloc(sizeof(BT));
BT *pE=(BT *)malloc(sizeof(BT));
pA->data='A';
pB->data='B';
pC->data='C';
pD->data='D';
pE->data='E';
pA->left=pB;
pA->right=pC;
pB->left=NULL;
pB->right=NULL;
pC->left=pD;
pC->right=NULL;
pD->left=NULL;
pD->right=pE;
pE->left=NULL;
pE->right=NULL;
return pA;
}BT *creat_tree()
{
char ch;
BT *t;
// printf("\n请输入二叉树的元素:\n");
fflush(stdin);
ch=getchar();
if(ch=='#'){
t=NULL;
}else{
t=(BT *)malloc(sizeof(BT));
assert(NULL!=t);
t->data=ch;
t->left=creat_tree();
t->right=creat_tree();
}
return t;
}void pre_traverse(BT *btree)
{
if(btree){
printf("%c\t",btree->data);
pre_traverse(btree->left);
pre_traverse(btree->right);
}
}void in_traverse(BT *btree)
{
if(btree){
in_traverse(btree->left);
printf("%c\t",btree->data);
in_traverse(btree->right);
}
}void post_traverse(BT *btree)
{
if(btree){
post_traverse(btree->left);
post_traverse(btree->right);
printf("%c\t",btree->data);
}
}int leaf_count(BT *btree)
{
if(btree){
leaf_count(btree->left);
leaf_count(btree->right);
if(btree->left==NULL && btree->right==NULL){
num++;
}
}
return num;
}int depth_tree(BT *btree)
{
int hl,hr,hm;
if(btree){
hl=depth_tree(btree->left);
hr=depth_tree(btree->right);
hm=hl>hr?hl:hr;
return(hm+1);
}else{
return 0;
}
} void print_leaf(BT *btree)
{
if(btree){
if(btree->left==NULL && btree->right==NULL){
printf("%c\t",btree->data);
}
print_leaf(btree->left);
print_leaf(btree->right);
}
}





















 9385
9385

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








