1185:炮兵阵地（友好详解）

描述

司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队。一个N*M的地图由N行M列组成，地图的每一格可能是山地（用"H" 表示），也可能是平原（用"P"表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

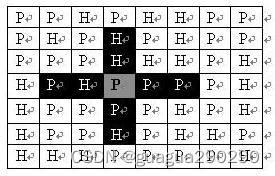
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。
现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。
输入
第一行包含两个由空格分割开的正整数，分别表示N和M；
接下来的N行，每一行含有连续的M个字符('P'或者'H')，中间没有空格。按顺序表示地图中每一行的数据。N <= 100；M <= 10。
输出
仅一行，包含一个整数K，表示最多能摆放的炮兵部队的数量。
样例输入
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
样例输出
6
来源
Noi 01

---

分析（有一些下标这里打不了就直接贴图了请谅解）

这种棋盘类型的问题+数据范围。看起来就像状态压缩。

因为相邻距离小于等于二的两列，不能互相攻击到，所以第i行，第i-1行，第i-2行不能产生冲突。所以得到（a & b）&& （a & c）&&（b & c）== 0 

而且在同一行内，大炮不能互相攻击到。
如果位置i有大炮，那么i+1和i+2的位置必须为0，两个同时为0 为true的话需要用||操作。

if ((state >> i & 1) && ((state >> i + 1 & 1) || (state i + 2 & 1)))
    return false;

状态初始化：
f[0][0][0] = 1

对于本题来说，直接开所有的状态空间，空间复杂度是 O(M×2ⁿ×2ⁿ)是会爆内存的

因此我们必须使用 滚动数组 进行优化

然后也可以预处理出来 相邻行之间的合法转移，也能避免掉一些不必要的不合法状态的枚举

---

代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>

using namespace std;

const int N = 110,M = 1 << 10;
int f[2][M][M]; // 第一维使用了滚动数组
vector<int>state; 
vector<int>pre[M];
int n,m;
int g[N]; // g[i]存第i行的地图
int cnt[M]; // cnt[i] 记录i中1的个数

bool check(int state)
{
    for(int i = 0 ; i < m ; i ++)
        if((state >> i & 1)&&((state >> i + 1 & 1)||(state >> i + 2 & 1)))return false;

    return true;    
}

int count(int state)
{
    int res=0;
    for(int i = 0 ; i < m ; i ++)res += state >> i & 1;
    return res;
}

int main()
{
    cin>>n>>m;

    for(int i = 1 ; i <= n ; i ++)  
        for(int j = 0 ; j < m ; j ++)
            {
                char c;
                cin>>c;
                if(c=='H')g[i] += 1 << j;
            }

    for(int i = 0 ; i < 1 << m ; i ++)
        if(check(i))
        {
            state.push_back(i);
            cnt[i] = count(i); 
        }

    //预处理合法状态能转移的状态    
    for (auto state_st : state)
        for (auto pre_st : state)
        	// 如果对应位没有同时为1
            if (!(state_st & pre_st))
                pre[state_st].push_back(pre_st);
                
    // f[i][j][k] :考虑前 i 层，且第 i 层状态是 j，第 i−1 层状态是 k 的方案
    // 枚举每一层
    for(int i = 1 ; i <= n + 2 ; i ++)
        for (auto i_st : state)//枚举当前层 
            if (!(g[i] & i_st))//第i层合法
                for (auto j_st : pre[i_st])//枚举上一层
                    if (!(g[i - 1] & j_st))//第i - 1层合法
                        for (auto u_st : pre[j_st])//枚举上二层
                            if (!(i_st & u_st))//判断当前行与前两行是否冲突
                                // 每次求一个最大值
                                f[i & 1][j_st][i_st] = max(f[i & 1][j_st][i_st] ,
                                                            f[i - 1 & 1][u_st][j_st] + cnt[i_st]);

    cout<<f[n + 2 & 1][0][0]<<endl;

    return 0;
}

给个赞和关注吧