1070:Deformed Wheel（变形车轮）（已翻译）（详解）（二分）

描述

The village's carpentry is located by a hill side. The carpenter's two little boys play with a piece of wood which looks like a deformed wheel with two identical convex polygon-shaped faces. One boy sets the wooden wheel on a slope at the hill top and let it roll down. The other boy is to quickly place himself at where he guesses the rolling wood would stop. Your program is to help him make the right guess.

More formally, we consider the wooden wheel as a simple convex polygon and we approximate the hill by a sequence of connected line segments with decreasing slopes. The slope of the last segment in the sequence is assumed to be zero, and the slope of the first segment is assumed to be a positive number. Initially, the wheel is placed on the hill such that there is at least one point of contact between the wheel and segments. For example in the following figure, the wheel in its initial position is drawn in solid lines, while the final position is drawn in dashed lines.

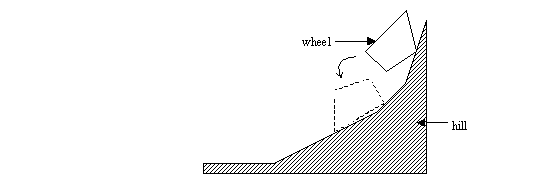
At any instant, the wheel rotates around one of its vertices, say P, if the y-coordinate of its center of gravity is decreased (note that this condition is necessary at any instant during the motion). It can be easily shown that at any instant, there is at most one such vertex. Rotation around P is stopped when the wheel touches a segment. The motion continues until no vertex can be found such that the wheel can rotate around it. At any instant, assume that changing the position of the center of gravity in any direction for at most 10-5 units, does not affect the stability of the wheel. Also assume that the friction between the wheel and the surface of the hill is so high that the wheel never slides on the surface.

这个村子的木工厂坐落在山边。木匠的两个小男孩在玩一块木头，这块木头看起来像一个变形的轮子，有两个相同的凸多边形面。一个男孩把木轮放在山顶的斜坡上，让它滚下来。另一个男孩快速地把自己放在他猜想的滚动的木头会停止的地方。你的计划是帮助他做出正确的猜测。更正式地说，我们认为木轮是一个简单的凸多边形，我们通过一系列连接的线段与斜率递减的山近似。序列中最后一段的斜率假设为零，第一段的斜率假设为正数。最初，车轮被放置在山丘上，以便在车轮和部件之间至少有一个接触点。例如，在下图中，轮子的初始位置是用实线描绘的，而最终位置是用虚线描绘的。在任何时刻，轮子都会绕着它的一个顶点旋转，比如说 P，如果它的重心的 y 坐标减小的话(注意，这个条件在运动过程中的任何时刻都是必要的)。可以很容易地证明，在任何时刻，最多只有一个这样的顶点。当车轮接触到一个部件时，围绕 P 的旋转就停止了。这种运动一直持续到找不到顶点为止，这样轮子就可以绕着它旋转。在任何时候，假设改变重心的位置在任何方向上最多10-5个单位，不影响车轮的稳定性。同时假设车轮与山体表面之间的摩擦力非常大，以至于车轮从未在山体表面上滑动过。

输入

The first line of the input contains a single integer t (1 <= t <= 10), the number of test cases, followed by the input data for each test case. In the first line of each test case there is an integer n (1 <= n <= 10), that indicates the number of the wheel vertices. In each of the next n lines, there is a pair of numbers which are x and y coordinates of the initial position of a vertex. After this, there is a single line containing the initial x and y coordinates of the center of gravity of the wheel. You can assume that the center of gravity is inside or on the boundary of the polygon (note that the given center of gravity is not necessarily computable from wheel's geometric shape). Next lines of the test data will describe the shape of the hill. The surface of the hill is approximated with a series of line segments with decreasing slopes ending with a horizontal line segment. For each segment, there is a line containing length and slope of a segment (both of them are real numbers). The lines are ordered in decreasing slope (The last line of this part of the input has slope zero). You can assume that the last (horizontal) line is long enough that the wheel would not pass its end. In the last line of the test case, there is a line containing the x and y coordinates of the right end-point of the first segment. All coordinates and slopes are real numbers.

输入的第一行包含一个整数 t (1 < = t < = 10) ，即测试用例的数量，然后是每个测试用例的输入数据。在每个测试用例的第一行中，有一个整数 n (1 < = n < = 10) ，表示轮子顶点的数目。在接下来的 n 行中，有一对数字，它们是顶点初始位置的 x 和 y 坐标。在此之后，有一条包含轮子重心初始 x 和 y 坐标的直线。你可以假设重心在多边形的内部或边界上(注意，给定的重心不一定能从轮子的几何形状计算出来)。测试数据的下一行将描述小山的形状。山的表面是近似的一系列线段与减少斜率结束与水平线段。对于每个段，都有一条包含段的长度和斜率的直线(它们都是实数)。这些线以斜率递减的方式排列(输入部分的最后一行的斜率为零)。您可以假定最后一条(水平)线的长度足以使车轮不会通过它的末端。在测试用例的最后一行中，有一行包含第一段右端点的 x 和 y 坐标。所有的坐标和斜率都是实数。

输出
For each test case, there should be a single line in the output , containing two numbers which are x and y coordinates of the wheel's center of gravity. Round the numbers in the output to 3 digits after decimal point.

对于每个测试用例，输出中应该有一条线，其中包含两个数字，即车轮重心的 x 和 y 坐标。将输出中的数字四舍五入到小数点后的3位。

样例输入
1
4
40 30
30 37
24 30
30 26
27 29
30 1
100 0
40 30
样例输出
28.854 20.031
来源
Tehran 2001

---

分析（一次就AC了，有点膨胀，出篇详解）

首先我们先把问题简化一下，我们先研究一个点绕另一个点旋转一定角度的问题。已知A点坐标(x1,y1)，B点坐标(x2,y2)，我们需要求得A点绕着B点旋转θ度后的位置。

A点绕B点旋转θ角度后得到的点，问题是我们要如何才能得到A’ 点的坐标。（向逆时针方向旋转角度正，反之为负）研究一个点绕另一个点旋转的问题，我们可以先简化为一个点绕原点旋转的问题，这样比较方便我们的研究。之后我们可以将结论推广到一般的形式上。

令B是原点，我们先以A点向逆时针旋转为例，我们过A’ 做AB的垂线，交AB于C，过C做x轴的平行线交过A’ 做x轴的垂线于D。过点C做x轴的垂线交x轴于点E。

令A的坐标(x,y)，A’ 坐标(x1,y1)，B的坐标(0,0)。我们可以轻松的获取AB的长度，而且显而易见A’ B长度等于AB。假设我们已知θ角的大小那么我们可以很快求出BC和A’ C的长度。BC=A’ B x cosθ，A’ C=A’ B x sinθ。

因为∠A’ CB和∠DCE为直角（显然的结论），则∠A’ CD +∠DCB =∠ECD +∠DCB=90度。

则∠A’ CD=∠ECD，∠A’ DC=∠CEB=90度，因此可以推断⊿CA’ D ∽⊿CBE。由此可以退出的结论有：

BC/BE=A’ C/A’ D和BC/CE=A’ C/CD

当然了DC和A’ D都是未知量，需要我们求解，但是我们却可以通过求出C点坐标和E点坐标间接获得A’ C和CD的长度。我们应该利用相似的知识求解C点坐标。

C点横坐标等于：((|AB| x cosθ) / |AB|) * x = x*cosθ

C点纵坐标等于：((|AB| x cosθ) / |AB|) * y = y*cosθ

则CE和BE的的长度都可以确定。

我们可以通过相⊿CA’ D ∽⊿CBE得出：

AD = x * sinθ DC = y * sinθ

那么接下来很容易就可以得出：

x1 = xcosθ- y * sinθ y1 = ycosθ + x * sinθ

则A’ 的坐标为(xcosθ- y * sinθ, ycosθ + x * sinθ)

我们可以这样认为：对于任意点A(x,y)，A非原点，绕原点旋转θ角后点的坐标为：(xcosθ- y * sinθ, ycosθ + x * sinθ)

接下来我们对这个结论进行一下简单的推广，对于任意两个不同的点A和B（对于求点绕另一个点旋转后的坐标时，A B重合显然没有太大意义），求A点绕B点旋转θ角度后的坐标，我们都可以将B点看做原点，对A和B进行平移变换，计算出的点坐标后，在其横纵坐标上分别加上原B点的横纵坐标，这个坐标就是A’ 的坐标。

推广结论：对于任意两个不同点A和B，A绕B旋转θ角度后的坐标为：

(Δxcosθ- Δy * sinθ+ xB, Δycosθ + Δx * sinθ+ yB )

注：xB、yB为B点坐标。

结论的进一步推广：对于任意非零向量AB（零向量研究意义不大），对于点C进行旋转，我们只需求出点A和B对于点C旋转一定角度的坐标即可求出旋转后的向量A’ B’ ，因为向量旋转后仍然是一条有向线段。同理，对于任意二维平面上的多边形旋转也是如此。

---

代码

#include<cstdio>
#include<cmath>
#include<vector>
using namespace std;
typedef struct{
	double x,y;
}POINT;
int n;
const double pi=3.1415926;
//当前点的位置
POINT p[10],g;
//存储长度和斜率
vector<double> vl,vs;
//存储每条直线的起点和斜率.
vector<POINT> vp;

inline double dis(POINT p1,POINT p2)
{
	return sqrt( (p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y) );
}

inline double dot(POINT p1,POINT p2,POINT p3)
{
	return (p3.x-p2.x)*(p1.x-p2.x)+(p3.y-p2.y)*(p1.y-p2.y);
}

double theta(POINT p2,POINT p1)
{
	double dx=p2.x-p1.x,dy=p2.y-p1.y,ret;
	if(dx==0)
	{
	
		if(dy>0)
			return	pi/2;
		else
		    return 1.5*pi;
	}
	else
	{
		ret=atan(dy/dx);
		if(dx>0)
		{
			if(dy>=0)
				return ret;
			else
				return 2*pi+ret;
		}
		else
			return pi+ret;	
	}
}
int main()
{
	int T;
	//cur_v,cur_l:当前旋转点所在的顶点和线段
	int i,j,cur_v,cur_l,flag;
	//dthe:旋转角度;tthe:角度变量
	double length,slope,dx,A,B,C,b,dthe,tthe,len;
	POINT tp;

	scanf("%d",&T);
	while(T--)
	{
		scanf("%d",&n);
		//input:输入多边形的顶点
		for(i=0;i<n;i++)
			scanf("%lf%lf",&p[i].x,&p[i].y);
	    scanf("%lf%lf",&g.x,&g.y);

		vl.clear();
		vs.clear();
        while(1)
		{
			scanf("%lf%lf",&length,&slope);
			vl.push_back(length);
			vs.push_back(slope);
			if(slope==0)
				break;
		}
		//第一条线段的右端点
		scanf("%lf%lf",&tp.x,&tp.y);
		vp.clear();
		vp.push_back(tp);
		for(i=1;i<vs.size();i++)
		{
			dx=vl[i-1]/sqrt(1+vs[i-1]*vs[i-1]);
			tp.x=vp[i-1].x-dx;
			tp.y=vp[i-1].y-dx*vs[i-1];
			vp.push_back(tp);

		}
		for(i=0;i<vl.size();i++)
		{
			for(j=0;j<n;j++)
				if( fabs( vs[i] * ( p[j].x - vp[i].x ) + vp[i].y - p[j].y ) <= 1e-6 )
				{
					cur_l=i;
					cur_v=j;
					break;
				}
			if(j<n)
				break;
		}
    	//上面得到的信息是旋转点在第i坡上,是多边形的第j个顶点
		if(vl.size()==1)
		{
			if( g.x > p[cur_v].x )
				flag = 1;
			else if(g.x < p[cur_v].x)
				flag = -1;
			else
				break;
			while(1)
			{
		
				//找出以p[cur_v]为原点的偏移角度最大的点
				tthe=100;
				for(i=0;i<n;i++)
					if( i!=cur_v && tthe - flag*theta(p[i],p[cur_v]) > 1e-9)
					{
						tthe = flag*theta(p[i],p[cur_v]);
						j = i;
					}
				len = dis(p[j],p[cur_v]);
				tp.x = p[cur_v].x + flag*len;
				tp.y = p[cur_v].y;
				dthe = theta(tp,p[cur_v]) - theta(p[j],p[cur_v]);
			
				for(i=0;i<n;i++)
				{
					len=dis(p[cur_v],p[i]);
					tthe=dthe+theta(p[i],p[cur_v]);
					p[i].x=p[cur_v].x+len*cos(tthe);
					p[i].y=p[cur_v].y+len*sin(tthe);
				}
				
				len=dis(g,p[cur_v]);
				tthe=dthe+theta(g,p[cur_v]);
				g.x=p[cur_v].x+len*cos(tthe);
				g.y=p[cur_v].y+len*sin(tthe);
				
				cur_v = j;
				if(flag==1 && g.x <= p[cur_v].x)
					break;
                if(flag==-1 && g.x >= p[cur_v].x)
					break;
			}
		}
		else
		{
			while(1)
			{
					
				//找到下一个旋转点
				//找出以p[cur_v]为原点的偏移角度最大的点
				tthe=-100;
				for(i=0;i<n;i++)
					if(i!=cur_v && tthe - theta(p[i],p[cur_v]) < 1e-9)
					{
						tthe = theta(p[i],p[cur_v]);
						j = i;
					}
			
				len=dis(p[j],p[cur_v]);
				for( ; cur_l+1<vl.size() && dis(p[cur_v],vp[cur_l+1])<len ; )
					cur_l++;
				//A*x^2+B*x+C=0;
				b=vp[cur_l].y-vs[cur_l]*vp[cur_l].x;
				A=1+vs[cur_l]*vs[cur_l];
				B=vs[cur_l]*(b-p[cur_v].y)-p[cur_v].x;
				B*=2;
				C=p[cur_v].x*p[cur_v].x;
				C+=(b-p[cur_v].y)*(b-p[cur_v].y)-len*len;
				//取值小的那个,并把(-B-sqrt(B^2-4*A*C))/2/A=>2*C/(-B+sqrt(B^2-4*A*C))
				tp.x=2*C/(-B+sqrt(B*B-4*A*C));
				tp.y=vs[cur_l]*tp.x+b;
			
				//将每个点都按一定角度旋转
				dthe = theta(tp,p[cur_v]) - theta(p[j],p[cur_v]);
				for(i=0;i<n;i++)
				{
					len=dis(p[cur_v],p[i]);
					tthe=dthe+theta(p[i],p[cur_v]);
					p[i].x=p[cur_v].x+len*cos(tthe);
					p[i].y=p[cur_v].y+len*sin(tthe);
				}
				//
				//len=dg[cur_v];
				len=dis(g,p[cur_v]);
				tthe=dthe+theta(g,p[cur_v]);
				g.x=p[cur_v].x+len*cos(tthe);
				g.y=p[cur_v].y+len*sin(tthe);
				//判断是否还会旋转
               	if( g.x >= p[j].x )
					break;
				cur_v = j;
			}
		}
		printf("%.3lf %.3lf\n",g.x,g.y);
	}
	return 0;
}

给个赞和关注吧