AES算法分析与实现

                                    AUTHOR:   Jeffrey.zhu

                                    BLOG：http://blog.csdn.net/gueter/

 

 

 

 

 

 

 

AES算法的主要数学基础是抽象代数，其中算法中的许多运算是按单字节（8bits）和4字节（32bits）定义的，单字节可看成有限域GF(2⁸)中的一个元素，而4字节则可以看成系数在GF(2⁸)中并且次数小于4的多项式（亦可以理解为：GF(256⁴)），单字节上的运算有两种：有限域GF(2⁸)上一个8次不可约多项式的模加、点乘（为方便代码实现，推出了X乘的概念），其中，这个不可约多项式为：m(x)= x⁸+x⁴+x³+x+1，类似地，4字节运算也分为两种：模加、乘法（为方便代码实现，推出了模乘的概念），而此时使用的模取M(x)=x⁴+1，由于x⁴+1=( x²+1)( x²+1)= ( x+1) ( x+1) ( x+1) ( x+1)，即非不可约，导致非0多项式乘法逆元（逆元求取主要用到了欧几里德（Euclid）算法）不一定存在，所以在AES算法中，只限于乘一个固定的有逆元的多项式：a(x)={03}x³+{01}x²+{01}x+{02}。

AES（128bits密钥）主要加解密流程如下图所示：

 

 

 

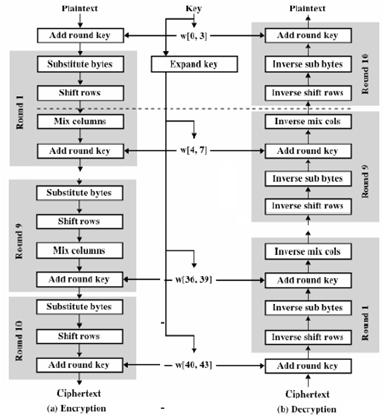
图中左边是加密流程，右边是解密流程，其中，Plaintext为明文，Ciphertext为密文，密钥长度可变，可指定为128、192、256比特，不同密钥长度决定了加解密算法的轮数（128位：10轮，192位：12轮，256位：14轮），算法征集之初，6轮迭代便可抵抗当时世界上已知的所有攻击，AES标准中至少留了4轮余量，按照这种说法，可以推知轮数越多，AES破解难度越大，也就是密钥越长越安全，所以今年8月份有人说256bits密钥长度的AES算法被破解，而128bits未被破解是没有根据的。

理解AES需要知道以下两个概念：