随机森林总结

2.2 随机森林

2.2.1 集成学习

1 概述

集成学习本身不是一个单独的机器学习算法，而是通过构建并结合多个机器学习器来完成学习任务。也就是我们常说的“博采众长”。集成学习可以用于分类问题集成，回归问题集成，特征选取集成，异常点检测集成等等，可以说所有的机器学习领域都可以看到集成学习的身影。本文就对集成学习方法进行简单的总结和概述。

集成学习有两个主要的问题需要解决，第一是如何得到若干个个体学习器，第二是如何选择一种结合策略，将这些个体学习器集合成一个强学习器。

2 集成学习之结合策略

1. 个体学习器已知的情况下

首先，我们介绍blending，blending就是将所有已知的个体学习器 g(t) 结合起来，发挥集体的智慧得到 强学习器G 。值得注意的一点是这里的 g(t) 都是已知的。blending通常有三种形式：

uniform：简单地计算所有g(t)的平均值

non-uniform：所有g(t)的线性组合

conditional：所有g(t)的非线性组合

其中，uniform采用投票、求平均的形式更注重稳定性，而non-uniform和conditional追求的更复杂准确的模型，但存在过拟合的危险。

1. 个体学习器未知的情况下

刚才讲的blending是建立在所有 g(t) 已知的情况。那如果所有个体学习器 g(t) 未知的情况，对应的就是学习法，做法就是一边学 g(t) ，一边将它们结合起来。学习法通常也有三种形式（与blending的三种形式一一对应）：

Bagging：通过bootstrap方法，得到不同g(t)，计算所有g(t)的平均值

AdaBoost：通过bootstrap方法，得到不同g(t)，所有g(t)的线性组合

Decision Tree：通过数据分割的形式得到不同的g(t)，所有g(t)的非线性组合

除了这些基本的集成模型之外，我们还可以把某些模型结合起来得到新的集成模型。

1. Bagging与Decision Tree结合起来组成了Random Forest。Random Forest中的Decision Tree是比较“茂盛”的树，即每个树的 g(t) 都比较强一些。
2. AdaBoost与Decision Tree结合组成了AdaBoost-DTree。AdaBoost-DTree的Decision Tree是比较“矮弱”的树，即每个树的gt都比较弱一些，由AdaBoost将所有弱弱的树结合起来，让综合能力更强。
3. GradientBoost与Decision Tree结合就构成了经典的算法GBDT。

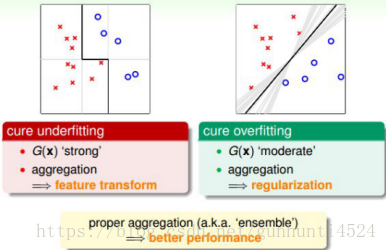
集成的核心是将所有的 g(t) 结合起来，融合到一起，即集体智慧的思想。这种做法之所以能得到很好的模型 G ，是因为集成具有两个方面的优点：cure underfitting和cure overfitting。

第一，集成 models 有助于防止欠拟合（underfitting）。它把所有比较弱的 g(t) 结合起来，利用集体智慧来获得比较好的模型 G 。集成就相当于是特征转换，来获得复杂的学习模型。

第二，集成 models 有助于防止过拟合（overfitting）。它把所有 g(t) 进行组合，容易得到一个比较中庸的模型，类似于SVM的最大间隔一样的效果，从而避免一些极端情况包括过拟合的发生。从这个角度来说，集成起到了正则化的效果。

由于集成具有这两个方面的优点，所以在实际应用中集成 models 都有很好的表现。

3 集成学习之Bootstrap

自助法(bootstrap)是统计学的一个工具，思想就是从已有数据集 D 中模拟出其他类似的样本 Dt 。

自助法在数据集较小、难以有效划分训练/测试集时很有用；此外，自助法能从初始数据集中产生多个不同的训练集，这对集成学习等方法有很大的好处。然而，自助法产生的数据集改变了初始数据集的分布，这会引入估计偏差。因此，在初始数据量足够时，留出法和交叉验证法更常用。

 

根据个体学习器的生成方式，目前集成学习分为两大类：

个体学习器之间存在强依赖关系、必须串行生成的序列化方法。代表是 Boosting；

个体学习器之间不存在强依赖关系、可同时生成的并行化方法。代表是 Bagging 和随机森林（Random Forest）。

2.2.2 Bagging

前面提到，想要集成算法获得性能的提升，个体学习器应该具有独立性。虽然 “独立” 在现实生活中往往无法做到，但是可以设法让基学习器尽可能的有较大的差异。

Bagging 给出的做法就是对训练集进行采样，产生出若干个不同的子集，再从每个训练子集中训练一个基学习器。由于训练数据不同，我们的基学习器可望具有较大的差异。

Bagging 是并行式集成学习方法的代表，采样方法是自助采样法（bootstrap），用的是有放回的采样。初始训练集中大约有 63.2% 的数据出现在采样集中。

Bagging 在预测输出进行结合时，对于分类问题，采用简单投票法；对于回归问题，采用简单平均法。

Bagging 优点：

 

高效。Bagging 集成与直接训练基学习器的复杂度同阶；

Bagging 能不经修改的适用于多分类、回归任务；

包外估计。使用剩下的样本作为验证集进行包外估计（out-of-bag estimate）。

Bagging 主要关注降低方差。（low variance）

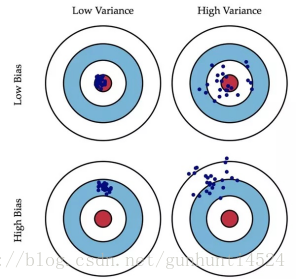
偏差（bias）：描述的是预测值（估计值）的期望与真实值之间的差距。偏差越大，越偏离真实数据，如上图第二行所示。

方差（variance）：描述的是预测值的变化范围，离散程度，也就是离其期望值的距离。方差越大，数据的分布越分散，如上图右列所示。

2.2.3 随机森林（Random Forest）

原理

随机森林（Random Forest）是 Bagging 的一个变体。Ramdon Forest 在以决策树为基学习器构建 Bagging 集成的基础上，进一步在决策树的训练过程中引入随机属性选择。

具体构造过程

1.从原始训练集中使用Bootstraping方法随机有放回采样选出m个样本，共进行n_tree次采样，生成n_tree个训练集

2.对于n_tree个训练集，我们分别训练n_tree个决策树模型

3.对于单个决策树模型，假设训练样本特征的个数为n，那么每次分裂时根据信息增益/信息增益比/基尼指数选择最好的特征进行分裂

4.每棵树都一直这样分裂下去，直到该节点的所有训练样例都属于同一类。在决策树的分裂过程中不需要剪枝

5.将生成的多棵决策树组成随机森林。对于分类问题，按多棵树分类器投票决定最终分类结果；对于回归问题，由多棵树预测值的均值决定最终预测结果。

 

分类：简单投票法；

回归：简单平均法。

优缺点

优点

1）具有极好的准确率

2）能够有效地运行在大数据集上

3）能够处理具有高维特征的输入样本，而且不需要降维

4）两个随机性的引入对随机森林的分类性能至关重要。由于它们的引入，使得随机森林不容易陷入过拟合，并且具有很好得抗噪能力

（随机森林的随机性体现在每棵树的训练样本是随机的，树中每个节点的分裂属性集合也是随机选择确定的。）

5）对数据的适应能力强，可以处理离散和连续的，无需要规范化；

缺点：

在噪声较大的时候容易过拟合。

当随机森林中的决策树个数很多时，训练时需要的空间和时间会较大

bagging和boosting

Bagging和Boosting都是将已有的分类或回归算法通过一定方式组合起来，形成一个性能更加强大的分类器，更准确的说这是一种分类算法的组装方法。即将弱分类器组装成强分类器的方法。

首先介绍Bootstraping，即自助法：它是一种有放回的抽样方法（可能抽到重复的样本）

1.Bagging (bootstrap aggregating)

Bagging即套袋法，其算法过程如下：

A）从原始样本集中抽取训练集。每轮从原始样本集中使用Bootstraping的方法抽取n个训练样本（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中）。共进行k轮抽取，得到k个训练集。（k个训练集之间是相互独立的）

 

B）每次使用一个训练集得到一个模型，k个训练集共得到k个模型。（注：这里并没有具体的分类算法或回归方法，我们可以根据具体问题采用不同的分类或回归方法，如决策树、感知器等）

C）对分类问题：将上步得到的k个模型采用投票的方式得到分类结果；对回归问题，计算上述模型的均值作为最后的结果。（所有模型的重要性相同）

2、Boosting

其主要思想是将弱分类器组装成一个强分类器。在PAC（概率近似正确）学习框架下，则一定可以将弱分类器组装成一个强分类器。

关于Boosting的两个核心问题：

1）在每一轮如何改变训练数据的权值或概率分布？

通过提高那些在前一轮被弱分类器分错样例的权值，减小前一轮分对样例的权值，来使得分类器对误分的数据有较好的效果。

2）通过什么方式来组合弱分类器？

通过加法模型将弱分类器进行线性组合，比如AdaBoost通过加权多数表决的方式，即增大错误率小的分类器的权值，同时减小错误率较大的分类器的权值。而提升树通过拟合残差的方式逐步减小残差，将每一步生成的模型叠加得到最终模型。

3.Bagging，Boosting的主要区别

样本选择上：Bagging采用的是Bootstrap随机有放回抽样；而Boosting每一轮的训练集是不变的，改变的只是每一个样本的权重。

样本权重：Bagging使用的是均匀取样，每个样本权重相等；Boosting根据错误率调整样本权重，错误率越大的样本权重越大。

预测函数：Bagging所有的预测函数的权重相等；Boosting中误差越小的预测函数其权重越大。

并行计算：Bagging各个预测函数可以并行生成；Boosting各个预测函数必须按顺序迭代生成。

4.算法组合

1）Bagging + 决策树 = 随机森林

2）AdaBoost + 决策树 = 提升树

3）Gradient Boosting + 决策树 = GBDT

 

随机森林python实现

参数说明：

最主要的两个参数是n_estimators和max_features。

n_estimators：表示森林里树的个数。理论上是越大越好。但是伴随着就是计算时间的增长。但是并不是取得越大就会越好，预测效果最好的将会出现在合理的树个数。

max_features：随机选择特征集合的子集合，并用来分割节点。子集合的个数越少，方差就会减少的越快，但同时偏差就会增加的越快。根据较好的实践经验。如果是回归问题则：

max_features＝n_features，如果是分类问题则max_features＝sqrt(n_features)。

 

如果想获取较好的结果，必须将max_depth＝None,同时min_sample_split=1。

同时还要记得进行cross_validated（交叉验证），除此之外记得在random forest中，bootstrap=True。但在extra-trees中，bootstrap=False。

---

from sklearn.tree import DecisionTreeRegressor

from sklearn.ensemble import RandomForestRegressor

import numpy as np



from sklearn.datasets import load_iris

iris=load_iris()

#print iris#iris的４个属性是：萼片宽度　萼片长度　花瓣宽度　花瓣长度　标签是花的种类：setosa versicolour virginica

print(iris['target'].shape)



rf=RandomForestRegressor()#这里使用了默认的参数设置

rf.fit(iris.data[:150],iris.target[:150])#进行模型的训练

#  

#随机挑选两个预测不相同的样本

instance=iris.data[[100,109]]

print(instance)

print('instance 0 prediction；',rf.predict(instance)[0])

print('instance 1 prediction；',rf.predict(instance)[1])

print(iris.target[100],iris.target[109])

---

[[6.3 3.3 6.  2.5]

 [7.2 3.6 6.1 2.5]]

instance 0 prediction； 2.0

instance 1 prediction； 2.0

2 2