Multi-Decoder Attention Model with Embedding Glimpse for Solving Vehicle Routing Problems-论文阅读

车辆路径问题的多解码器注意力模型与嵌入凝视方法

原文内容

摘要

我们提出了一种新颖的深度强化学习方法，用于学习车辆路径问题的构造启发式规则。具体而言，我们设计了一种多解码器注意力模型（MDAM），通过训练多个差异化策略，相比现有仅训练单一策略的方法，显著提高了寻获优质解的概率。针对MDAM的多样性特点，我们定制了集束搜索策略以充分挖掘其潜力。此外，基于路径构造的递归特性，我们在MDAM中创新性地引入了嵌入凝视层，通过提供更具信息量的嵌入表示来提升各策略的决策质量。在六类典型路径问题上的大量实验表明，本方法显著超越了当前最先进的基于深度学习的模型。

1 引言

路径问题（如旅行商问题TSP和带容量约束的车辆路径问题CVRP）作为组合优化问题的重要分支，在物流配送等领域具有广泛应用(Toth and Vigo 2014)。由于其组合特性，这类问题通常具有NP难特性(Applegate et al. 2006b)。虽然分支定界等精确算法(Fischetti, Toth, and Vigo 1994)能保证理论最优性，但指数级的最坏计算复杂度使其难以应对大规模问题。相比之下，基于启发式规则的近似算法能在多项式时间内找到接近最优的解，因而更具实用价值。

传统方法依赖人工设计的启发式规则，而现代深度学习方法(Bello et al. 2016; Dai, Dai, and Song 2016; Nazari et al. 2018; Kool, van Hoof, and Welling 2019; Chen and Tian 2019)则从数据中自动学习启发式规则。这些方法多采用编码器-解码器架构，通过逐步添加节点的方式构造解。其中编码器将节点信息映射为特征嵌入，解码器则预测每个构造步骤的节点选择概率。为提升解的质量，现有方法通过采样(Kool, van Hoof, and Welling 2019)或集束搜索(Nazari et al. 2018)从训练策略中生成多个解并选取最优。

然而现有研究存在两大局限：首先，解的多样性不足。对于VRP等组合问题，存在多个最优解，增加解的多样性将提高找到优质解的概率。但现有方法仅训练单一构造策略，仅依靠概率分布的随机性产生差异，这种多样性极为有限。其次，构造策略训练存在缺陷(Xin et al. 2020)。路径构造本质是系列节点选择子任务，已访问节点与后续决策无关。但现有模型(Kool, van Hoof, and Welling 2019; Bello et al. 2016)在各步骤解码时仍使用相同的节点嵌入，未能消除无关节点干扰，导致嵌入表示基于全局图而非当前子任务图，可能降低策略质量。

本文同步解决上述问题：第一，为提升多样性，提出多解码器注意力模型（MDAM）。该模型采用Transformer编码器(Vaswani et al. 2017)与参数独立的多注意力解码器，通过KL散度损失正则化迫使解码器学习差异化策略。基于MDAM设计了新型集束搜索方案，为各解码器维护独立搜索空间，充分保持解的多样性。第二，为提升单策略质量，利用路径问题的递归特性，在编码器顶层注意力中显式移除已访问节点，使解码器获得更精准的节点嵌入表示。

需要说明的是，与高度优化的传统求解器相比，本研究旨在探索深度学习模型在路径问题启发式规则学习中的潜力。与(Kool, van Hoof, and Welling 2019)类似，虽然聚焦TSP和CVRP，但方法可灵活扩展至含不同约束甚至不确定性的路径问题。在六类路径问题上的实验验证了提升多样性和消除无关节点的有效性。更重要的是，我们的模型显著优于当前最强的深度强化学习方法，在短时推理下展现出与传统非学习型启发式方法和成熟求解器相当或更优的性能。

2 相关工作

在现有学习构造启发式规则的模型中，Vinyals等人(2015)提出的指针网络(PtrNet)采用长短期记忆网络(LSTM)作为编解码器，通过监督学习求解TSP。但由于需要查询最优解标签，该方法仅适用于小规模问题。Bello等人(2016)改用REINFORCE算法训练PtrNet，摆脱了对真实标签的依赖，使模型能处理更大规模的TSP。不同于PtrNet采用LSTM顺序编码节点，Nazari等人(2018)使用置换不变层进行节点编码，并针对CVRP训练模型。他们通过集束搜索跟踪最有潜力的解来提升解质量。Kool等人(2019)采用Transformer模型编码节点，使用类指针注意力机制解码。该优雅模型通过从训练策略中采样1280个解，在多个路径问题上取得了当时最先进的成果。

部分研究未采用上述编解码器结构。Dai等人(2017)应用深度Q学习算法训练基于Structure2Vec的图神经网络，用于求解包括TSP在内的组合优化问题。然而TSP的完全连通特性使其图结构信息失效，导致性能不如依赖关键图信息的顶点覆盖、最大割等问题。不同于学习构造启发式，Chen和Tian(2019)提出NeuRewriter学习改进启发式，通过训练区域选择策略和规则选择策略对初始解进行迭代优化。在CVRP上，其性能超越Kool等人的采样结果。但NeuRewriter采用序列化改写操作，无法像我们的方法那样实现并行搜索。Hao Lu(2020)另辟蹊径，设计网络学习选择局部移动类型，并在每步改进时穷举搜索该类型的最佳贪婪移动。虽然解质量优异，但由于每步需对数万种局部移动进行穷举搜索，导致计算时间过长而缺乏实用性。

3 模型

3.1 多解码器注意力模型与搜索

为生成多样化解，我们提出多解码器注意力模型（MDAM），并设计定制化集束搜索策略，利用多解码器结构有效保持解集的多样性。

多解码器注意力模型
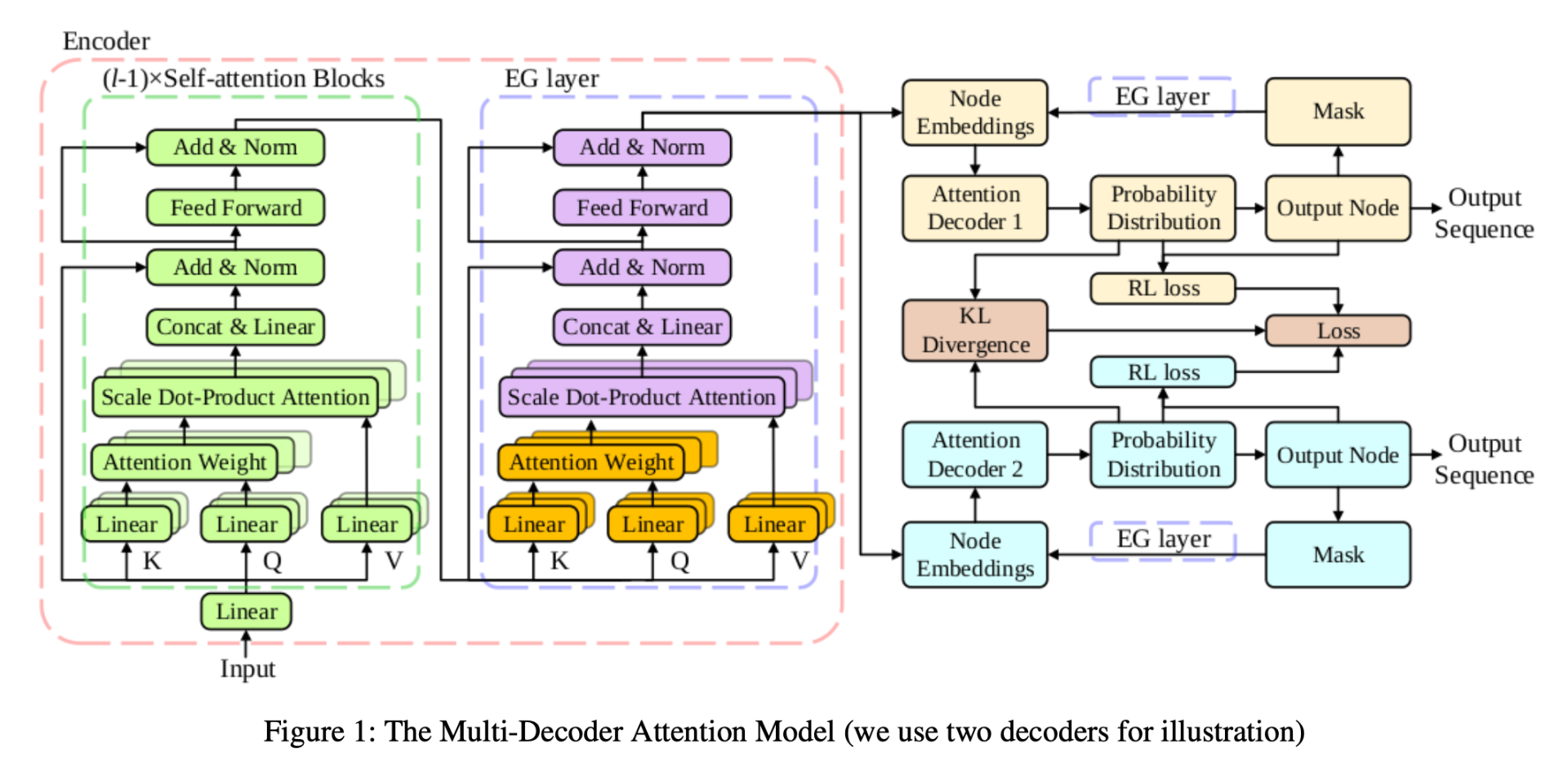
MDAM由1个编码器和多个结构相同但参数独立（unshared parameters）的解码器组成。编码器将TSP节点的二维坐标（其他路径问题可能包含需求量、奖励值等额外维度）转化为特征向量。每个解码器在解的构造过程中，基于节点嵌入生成各有效节点的访问概率分布。图1展示了MDAM架构（图示为双解码器），其中EG层将在后文详述。

编码器采用Transformer架构(Vaswani et al. 2017)，包含多个自注意力块，其核心是多头注意力层：

Query/Key/Value投影：
$$Q_i^h,K_i^h,V_i^h=W_Q^h{X}_i,W_K^h{X}_i,W_V^h{X}_i(1)$$

单头注意力计算：
$$A^h=\text{Attention}(Q^h,K^h,V^h)=\text{softmax}\left(\frac{Q^h{K^h}^T}{\sqrt{d_k}}\right)V^h(2)$$

多头输出拼接：
$$\text{Multihead}(Q,K,V)=\text{Concat}(A^1,...,A^H)W^O(3)$$

其中：

h ∈ {1,…,H} 表示注意力头索引

Xi ∈ ℝ^d 为节点i的嵌入向量

W^h_Q, W^h_K, W^h_V ∈ ℝ^{d×d_k} (d_k = d/H)

W^O ∈ ℝ^{d×d} 为输出投影矩阵

式(1)(2)对H个注意力头并行计算，其中Xi为节点i的d维嵌入，$W{Q}_h,W{K}_h,W{V}_h\in R^{d\times dk}（dk=d/H）$。注意力输出经拼接和$WO\in R^{d\times d}$投影后，通过跳跃连接(He et al. 2016)、批归一化(BN)(Ioffe and Szegedy 2015)及带ReLU激活的双线性投影层(FF)得到最终输出：

残差连接：
$${\hat{f}}_i=\text{BN}(X_i+{\text{Multihead}}_i(Q,K,V))(4)$$

前馈层：
$$f_i=\text{BN}({\hat{f}}_i+\text{FF}({\hat{f}}_i))(5)$$

设解码器数量为M，每个解码器m模拟节点选择概率Pm(yt|x,y1,…,yt-1)，其计算流程如下：

上下文嵌入：
$$f_c=\text{Concat}(\bar{f},f_{C0},f_{C_{t-1}})(6)$$

多头注意力重构：
$$g_c^m=\text{Multihead}(W_{gQ}^m{f}_c,W_{gK}^{m}f,W_{gV}^{m}f)(7)$$

概率计算：
$$\begin{array}{rl}{q}^m,k_i^m& =W_Q^m{g}_c^m,W_K^m{f}_i(8)\\ u_i^m& =10\cdot \tanh \left(\frac{{q^m}^T{k}_i^m}{\sqrt{d}}\right)(9)\\ P^m(y_t|x,y_{1:t-1})& =\text{softmax}(u^m)(10)\end{array}$$
其中fc为上下文嵌入，¯f为节点嵌入均值，fC0和fCt-1分别对应起始节点和当前节点嵌入（首步替换为可训练参数）。式(7)类似(Bello et al. 2016)中的glimpse操作，式(9)设置D=10以控制探索范围。

为促使解码器学习差异化构造模式，训练时最大化各解码器输出分布的KL散度：

$${\mathcal{D}}_{KL}=\sum _s\sum _{i=1}^M\sum _{j=1}^M\sum _y{P}^i(y|x,s)\log \frac{P^i(y|x,s)}{P^j(y|x,s)}(11)$$

定制化集束搜索
组合优化问题的解空间呈指数级增长，但通过确定性指标（如路径长度）可高效评估少量解。然而传统采样和集束搜索难以维持解集多样性：同策略采样易产生重复解，而树形集束搜索所得解集变异度低且确定性高(Kool et al. 2019)。

我们提出面向MDAM的新型集束搜索方案：

对总束宽B，为每个解码器分配独立子束（束宽⌈B/M⌉）

同一解码器的子束内采用合并技术（merging technique）避免无效构造：

TSP示例：当两个部分解具有相同起始点、已访问节点集和当前位置时（即剩余子任务相同），保留部分路径较短者（图2步骤4中解1→2→4→5与1→4→2→5的合并情形）

CVRP扩展：需额外满足剩余车容量约束

合并时删除劣解，优解概率取两者最大值

虽然合并操作的计算开销随束宽呈平方增长，但由于采用分散子束策略（各子束规模较小），该问题得以缓解。

3.2 嵌入凝视层（Embedding Glimpse Layer）

在构造式启发方法中，模型需要以自回归方式输出一系列节点选择。已访问的节点与未来决策无关，若在所有构造步骤中基于相同的节点嵌入进行解码，可能导致性能下降。为提升解的质量，最理想的方式是在每步访问一个节点后，仅对未访问节点重新生成嵌入。然而，这种完整的逐步重嵌入计算成本极高。

为此，我们提出嵌入凝视层（EG层）来近似重嵌入过程。其设计灵感源于神经网络高层特征更具任务相关性的特性（例如CNN中，低层提取像素/边缘特征，高层提取语义特征）。我们假设注意力模型具有类似的层次特征提取范式，并依此设计EG层如下：

在包含l个自注意力块的编码器中，我们通过固定底层l-1个注意力层，并在顶层注意力层中屏蔽已访问节点的注意力权重，从而近似实现节点嵌入更新。EG层作为编码器的顶层注意力层，被所有解码器共享，其部分计算可预先完成（图1中橙色部分）：

$Q_i^h=W_Q^h{X}_i,K_i^h=W_K^h{X}_i,V_i^h=W_V^h{X}_i(12)$

$w^h(Q^h,K^h)=Q^h{K}^{h\top }/\sqrt{d_k}(13)$

在步骤t，通过将已访问节点集C_{t-1}的注意力权重设为-∞（图1紫色部分），实现动态掩码：

$A^h=\text{Attention}(Q^h,K^h,V^h)=\text{softmax}(w^h)V^h(14)$

$\text{Multihead}(Q,K,V)=\text{Concat}(A^1,...,A^H)W_O(15)$

随后通过式(4)(5)生成新节点嵌入，供解码器选择下一节点。之后，当需要决定访问哪个新节点时，可以通过新的掩码执行式(14)、(15)、(4)和(5)来获得新的节点嵌入。

EG层可视为通过"已访问节点不再相关"这一信息来修正节点嵌入。然而，每一步都运行EG层会产生额外的计算开销。为缓解此问题，我们每隔p步执行一次EG层。这是合理的，因为节点嵌入变化是渐进的，且每步仅移除一个节点。我们发现该技术能在几乎不增加推理时间的情况下持续提升性能。EG层可视为对(Xin et al. 2020)逐步思想的泛化，具有更好的计算效率。通过选择超参数p，我们可以使EG层的重嵌入次数在不同规模的问题中保持大致恒定。

3.3 训练

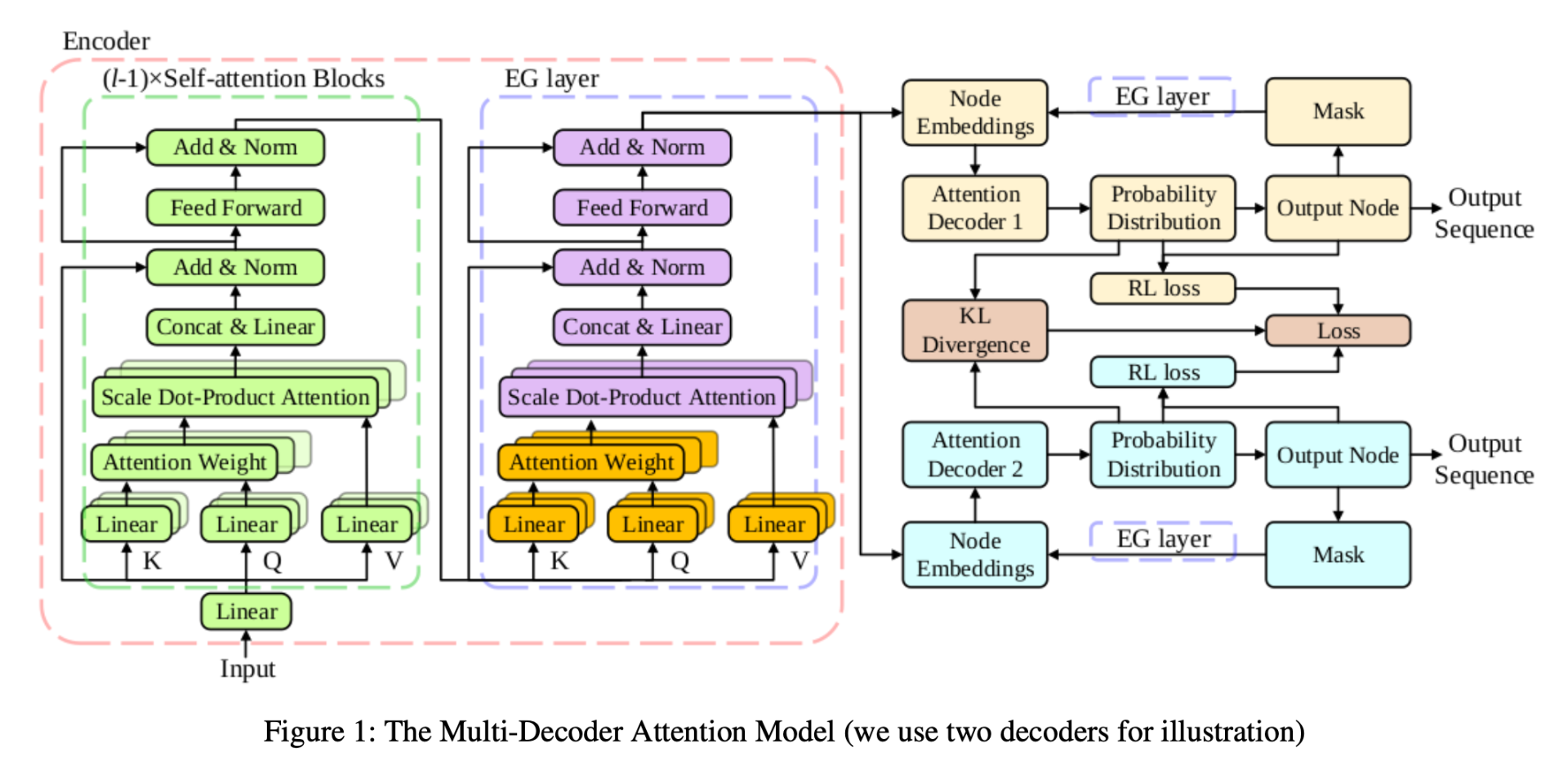
MDAM 的结构及其训练过程如图 1 所示。$l$ 层编码器由 $l-1$ 个注意力模块和一个我们此前介绍过的 EG 层组成。对于输入实例 $x$，多个解码器中的每一个都会独立采样一条轨迹 ${\pi }^m$，以获得基于相同贪心滚动基线的 REINFORCE 损失：

$$\nabla {\mathcal{L}}_{\text{RL}}(\theta |x)=\sum _m{\mathbb{E}}_{P_{\theta }^m({\pi }^m|x)}\left[\left(L({\pi }^m)-b(x)\right)\nabla \log P_{\theta }^m({\pi }^m|x)\right]\text{\hspace{1em}(16)}$$

其中 $L({\pi }^m)$ 是路径长度。我们采用的基线与 Kool, van Hoof, and Welling (2019) 中表现最好的类似。具体地，我们使用前若干 epoch 中参数最优的模型作为基线模型，对当前实例进行贪心解码以获取基线 $b(x)$：

b ( x ) = min ⁡ m L ( π m ′ = { y m ′ ( 1 ) , … , y m ′ ( T ) } ) (17) b(x) = \min_m L(\pi'_m = \{ y'_m(1), \dots, y'_m(T) \}) \tag{17} b(x)=mmin​L(πm′​={ym′​(1),…,ym′​(T)})(17)

$$y_m^{\prime }(t)=\arg \underset{y_t}{\max }{P}_{{\theta }^{\prime }}^m\left(y_t\mid x,y_m^{\prime }(1),\dots ,y_m^{\prime }(t-1)\right)\text{\hspace{1em}(18)}$$

其中 $\theta$ 是当前 MDAM 的参数，${\theta }^{\prime }$ 是来自上一 epoch 的固定基线模型参数，$m$ 是解码器的索引。

我们通过梯度下降来优化模型：

$$\nabla \mathcal{L}(\theta )=\nabla {\mathcal{L}}_{\text{RL}}(\theta |x)-k_{\text{KL}}\nabla D_{\text{KL}}\text{\hspace{1em}(19)}$$

其中 $k_{\text{KL}}$ 是 KL 损失的系数。理想情况下，应在训练期间为每个解码器遇到的每个状态计算一次 KL 损失以鼓励多样性。但为了避免高昂的计算成本，我们仅在第一个步骤上施加 KL 损失，原因如下：

• 首先，所有解码器的初始状态相同，即为空解，在此状态下 KL 损失既有意义又易于计算；
• 其次，对于同一实例，不同最优解通常在第一步就有不同选择，这对构造模式具有强影响。

4 实验

在本节中，我们在六个路径规划问题上进行了实验，以验证我们方法的有效性。其中，TSP 和 CVRP 是研究最广泛的问题。TSP 被定义为在给定每对城市之间距离的情况下，寻找一条最短路径，该路径访问每个城市一次并返回起始城市。CVRP 是 TSP 的推广，其起始城市必须为一个仓库，其他城市都有需求需由车辆服务。CVRP 中可以规划多条路线，每条路线对应一辆车辆，访问的城市总需求不能超过车辆容量，所有城市都需要被路线覆盖。

我们遵循已有工作（Kool, van Hoof, and Welling 2019；Nazari et al. 2018）生成了包含 20、50 和 100 个节点（城市）的实例，使用二维欧几里得距离来计算两个城市之间的距离，目标是最小化总旅行距离。城市位置的坐标是从 [0, 1] 区间的均匀分布中独立采样得到的。对于 CVRP，车辆容量分别固定为 30、40、50（对应 20、50、100 个城市的问题）。每个非仓库城市的需求从整数集合 {1…9} 中采样。

对于剩下的四个路径规划问题，即可分配送路径问题（SDVRP）、探险问题（OP）（Golden, Levy, and Vohra 1987）、奖励收集 TSP（PCTSP）（Balas 1989）和随机奖励收集 TSP（SPCTSP），设置与现有工作（Kool, van Hoof, and Welling 2019）保持一致，并在补充材料中介绍。需要注意的是，这些问题具有各自的约束，甚至包括随机因素（如 SPCTSP）。尽管如此，MDAM 足够灵活，能够通过在每一步屏蔽无效节点来处理这些特性。

超参数

我们通过逐元素投影将节点嵌入为 128 维向量。Transformer 编码器具有 3 层，每层特征维度为 128，使用 8 个注意力头，其中顶层作为 EG 层，前馈全连接层（公式 (5) 中的 FF）的隐藏维度为 512。我们选择 MDAM 中的解码器数量为 5，每个解码器使用 128 维向量和 8 个注意力头。对于 EG 层，我们将重新嵌入之间的步骤数设置为：TSP20、50、100 分别为 2、4、8，CVRP20、50、100 分别为 2、6、8，以加快评估速度。

按照（Kool, van Hoof, and Welling 2019），我们以每个 epoch 2500 次迭代、batch size 为 512（CVRP100 为 256 以适配 GPU 内存限制）进行训练，共训练 100 个 epoch。我们使用 Adam 优化器（Kingma and Ba 2014），学习率为 10^-4。KL 损失的系数 kKL 需要足够大，以保持不同解码器之间的多样性，但不能过大以至于损害每个解码器的性能。我们根据 TSP20 的实验将 kKL 设置为 0.01。我们的代码将很快发布。

4.1 对比研究

在这里，我们将我们的方法（MDAM）与现有的强大的基于深度学习的模型进行比较。为了测试，我们从与训练相同的分布中采样了 10,000 个实例。为计算最优性差距，我们使用精确求解器 Concorde（Applegate et al. 2006a）来获得 TSP 的最优解的目标值。而对于难以精确求解的 CVRP，我们遵循（Kool, van Hoof, and Welling 2019）使用最先进的启发式求解器 LKH3（Helsgaun 2017）来获得基准解。

对于 MDAM 的束搜索版本，我们使用 5 个解码器，每个解码器的 beam size 为 B=30 和 50（分别记为 bs30 和 bs50），即总束宽度分别为 B=150 和 250。需要注意的是，一些方法（例如 (Vinyals, Fortunato, and Jaitly 2015)、(Dai et al. 2017)、(Tsiligirides 1984) 和 (Deudon et al. 2018)）由于在 (Kool, van Hoof, and Welling 2019) 中报告的性能较差，因此未作为基线方法。我们也没有与 (Hao Lu 2020) 中的 L2I 进行比较，因为其计算时间过长。在没有任何实例并行化的情况下，我们的模型在 CVRP100 实例上以束宽 50 进行推理的平均时间为 6.7 秒，而 L2I 需要 24 分钟（Tesla T4）。

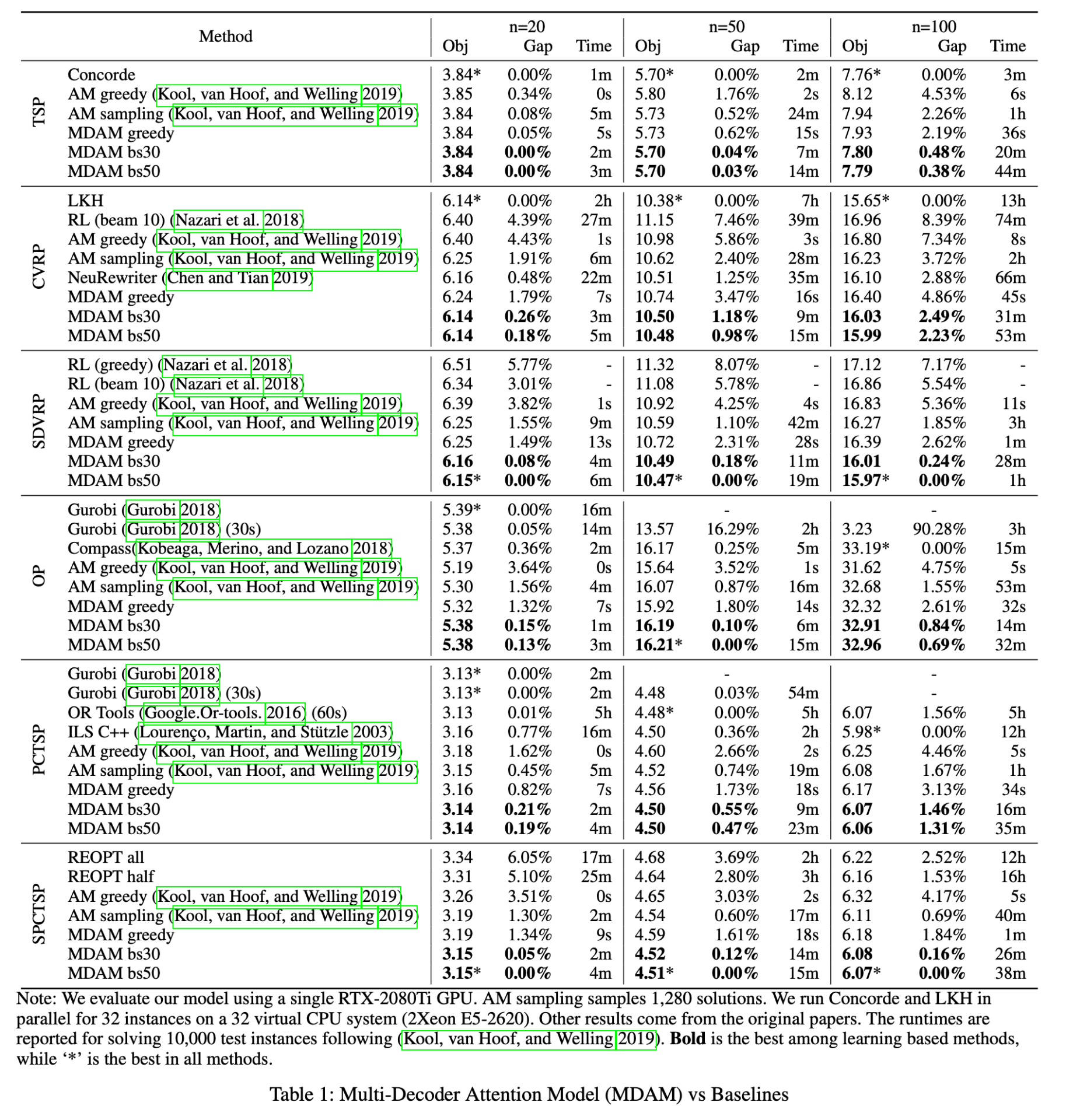
对于另外四个问题，我们将 MDAM 与 AM 及 (Kool, van Hoof, and Welling 2019) 中的其他强基线进行比较，具体细节在补充材料中介绍。结果总结于表 1。需要注意的是，除了 OP 旨在最大化沿途收集的奖赏外，所有问题的目标均为最小化。

我们可以观察到，在包含 20、50 和 100 个节点的所有六个路径问题上，MDAM 始终显著优于 AM（Kool, van Hoof, and Welling 2019）。为了避免大规模问题的极长计算时间，对于部分问题，我们使用带时间限制的精确求解器 Gurobi（2018）作为启发式方法。

在 CVRP 和 SDVRP 上，我们的 MDAM 使用贪心解码策略显著优于现有的贪心解码模型（Nazari et al. 2018；Kool, van Hoof, and Welling 2019）以及 RL（Nazari et al. 2018）的方法（标准束搜索版本）。通过束搜索策略，MDAM 不仅优于 AM（Kool, van Hoof, and Welling 2019）的采样版本，还优于 CVRP 上的改进型启发式 NeuRewritter（Chen and Tian 2019）。此外，增大束宽可以有效提升六个问题上的解质量，代价是推理时间增加。

对于与传统非学习方法的比较，值得注意的是，在大规模实例（如具有 100 个节点的 OP 和 PCTSP）中，MDAM 优于复杂的通用求解器 OR Tools 和带时间限制的 Gurobi，并显示出相对较好的可扩展性。对于某些问题（例如具有 50 个节点的 OP），MDAM 优于高度专业化的启发式求解器。

构造型启发式算法的一个理想特性是它们可以自然地处理不确定性，因为解是逐步构建的。相比之下，优化方法（例如 Gurobi、OR Tools 以及改进型启发式）需要某种形式的在线重新优化（REOPT）（Kool, van Hoof, and Welling 2019）来适应动态变化（如约束违背）。在 SPCTSP 中，每个节点的实际奖赏仅在访问后才知道，MDAM 明显优于 REOPT 策略（具体见补充材料）、AM 的贪心和采样方法。

在效率方面，虽然基线方法是在不同机器上运行的，但与现有的基于深度学习的方法相比，MDAM 的计算时间是可以接受的，特别是考虑到显著的性能提升。尽管 MDAM（以及所有深度模型）在某些问题上可能比高度专业化的求解器（例如 Concorde 在 TSP 上）慢，但总体上比传统算法快得多，同时具有可比的解质量。

4.2 消融实验

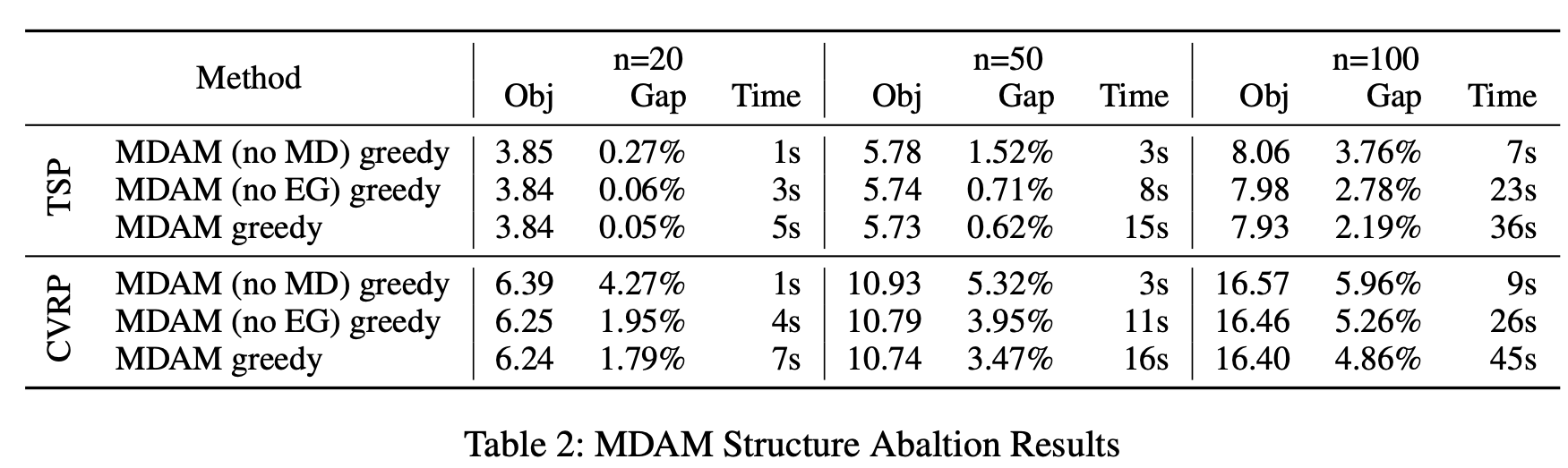
我们进一步以 TSP 和 CVRP 为测试平台，评估模型中不同组件的有效性。我们通过消融实验来评估多解码器结构（MD）和 Embedding Glimpse 层（EG）对贪心构造策略质量的贡献。我们在这里省略束搜索，因为它是一个独立技术，可以应用于任意给定的贪心解码策略。结果汇总于表 2。

我们可以观察到，无论是在何种实例设置下，MD 和 EG 都能持续提升学习到的构造策略的质量，这充分验证了我们设计的合理性。虽然 MD 可以显著提升性能，但会带来相对较长的推理时间；相比之下，EG 的改进幅度较小，但几乎不会增加额外计算负担。

4.3 MDAM 分析

为了展示每个解码器所学习到的不同构造模式的实用性，我们评估了每个解码器在 CVRP20 上使用贪心解码和束搜索（B=50）时的表现。图 3 展示了在贪心解码和搜索模式中，每个解码器找到最优解（胜出）和唯一最优解（单独胜出）的次数。

我们可以看到，在两个模式下，找到最优解的次数都高于唯一最优解的次数，说明多个解码器同时找到最优解的情况是普遍存在的。更重要的是，所有解码器的表现都相近，没有哪一个明显占优或完全无效，说明每个解码器在求解过程中确实发挥了作用。

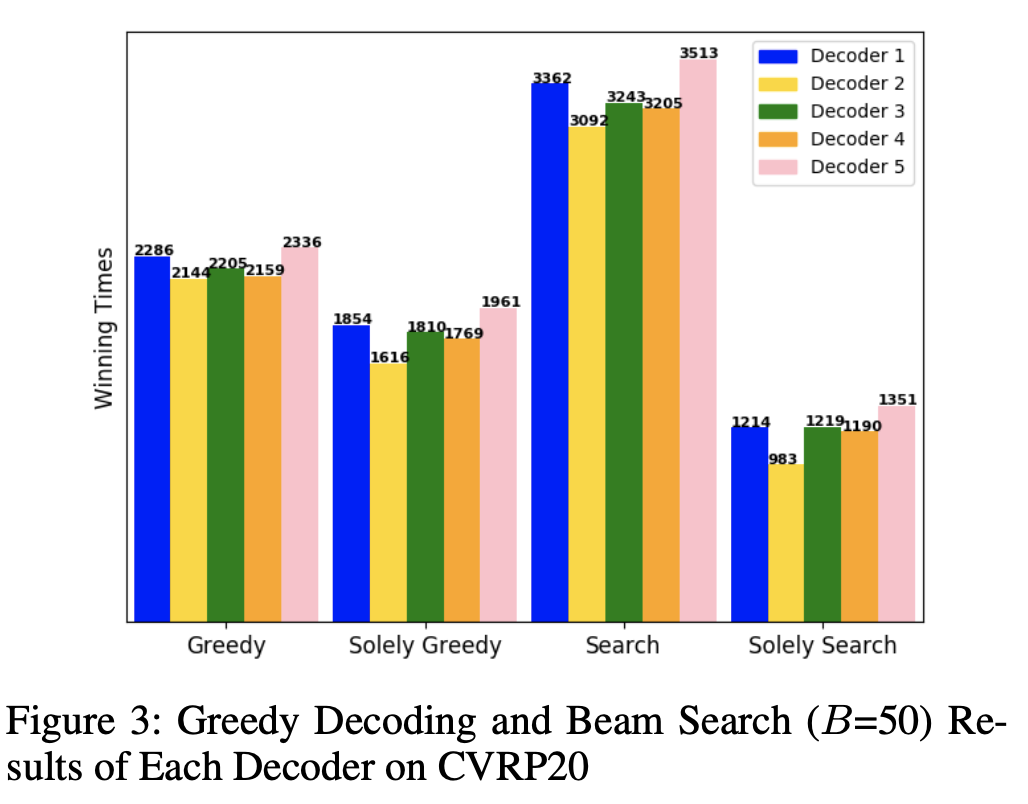
图 3：每个解码器在 CVRP20 上的贪心解码和束搜索（B=50）结果

在补充材料中，我们还进一步分析了 MDAM 的更多特性，包括我们为定制束搜索设计的合并技术的有效性，以及束搜索模式下不同解码器数量的影响。我们还与 AM 的一个更强版本进行了比较，以进一步验证 MDAM 的有效性。具体而言，我们调整 AM 采样时 softmax 输出函数的温度超参数，以提供更具多样性的解。

最后，我们展示了，与 AM 相比，MDAM 在更大规模问题（如包含 150 和 200 个节点的 CVRP）上具有更好的泛化能力。

5 结论与未来工作

本文提出了一种新颖的模型，用于学习路径问题的构造型启发式策略，并采用强化学习进行训练。该方法采用多解码器结构来学习不同的构造模式，并通过定制的束搜索策略加以利用。模型中引入了 Embedding Glimpse 层，使得解码器能获得更具信息量的嵌入表示。

我们的方法在六种路径问题中均优于现有的最先进深度学习方法，并能在合理时间内生成接近传统高优化度求解器的解。未来，我们计划通过允许解码器数量灵活变化，并使多个解码器协同决策（而非各自独立）来进一步改进我们的模型。

6 致谢

本研究得到了 ST Engineering-NTU Corporate Lab 的支持，资助来自 NRF corporate lab@university 计划。部分研究工作在新加坡电信-南洋理工大学企业人工智能实验室（SCALE@NTU）开展，该实验室是新加坡电信有限公司（Singtel）与南洋理工大学（NTU）合作设立的，资金来源于新加坡政府通过 Industry Alignment Fund - Industry Collaboration Projects Grant。

宋文获得了山东大学青年学者未来计划（项目编号：62420089964188）的部分资助。曹志光获得了中国国家自然科学基金（项目编号：61803104）的部分资助。

分析

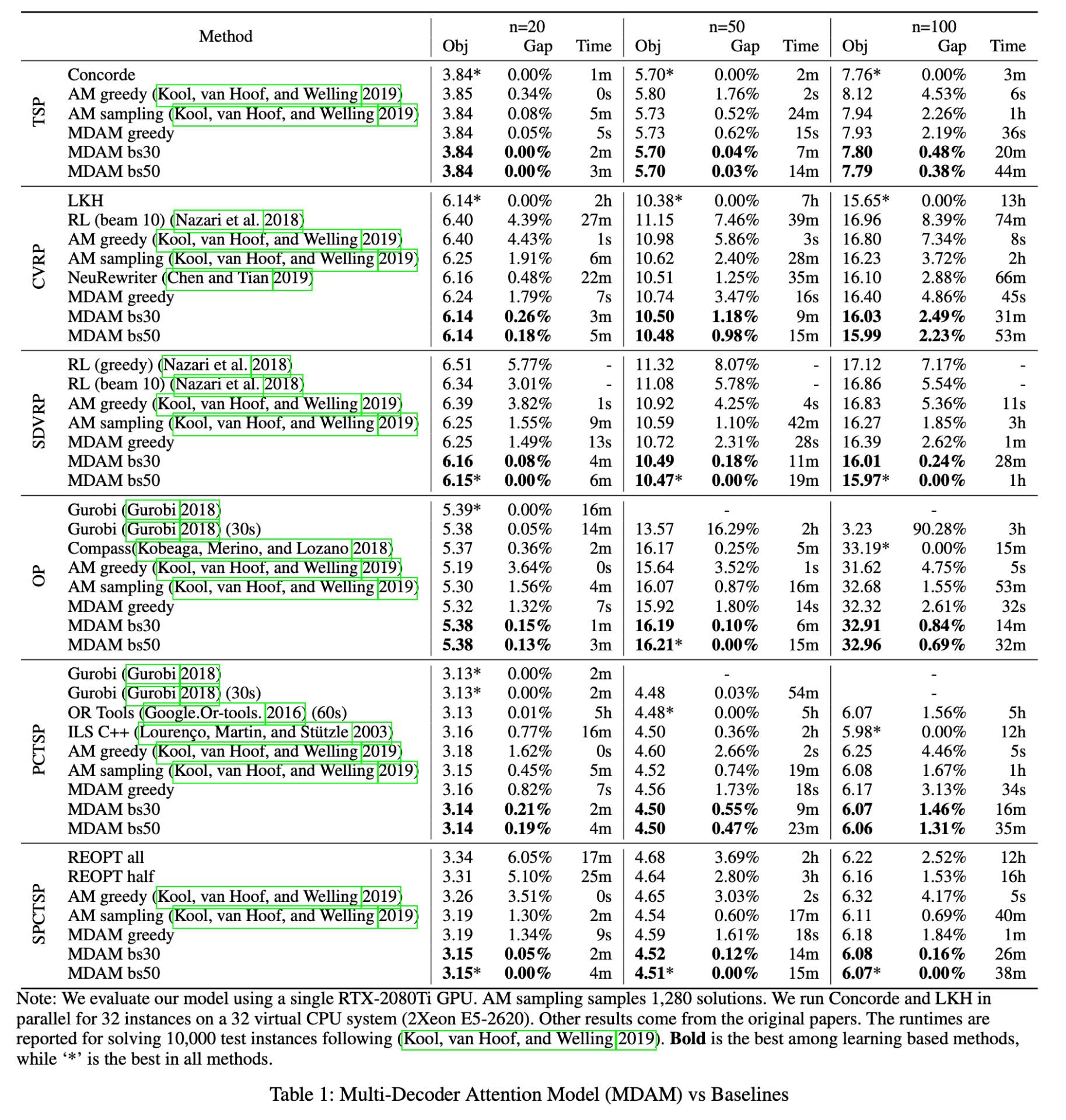
📊 表 1：Multi-Decoder Attention Model (MDAM) vs Baselines
该表展示了 MDAM 与多个基线方法在六类路径问题（TSP、CVRP、SDVRP、OP、PCTSP、SPCTSP）中的性能对比。每类问题中均给出了三种规模：n=20, n=50, n=100（即城市/节点数量）。
表格列说明：

•	Method：算法名称；
•	Obj：平均目标值（例如路径总长度）；
•	Gap：与最优解之间的相对误差（%）；
•	Time：每个实例的平均求解时间。

📌 重点观察：

•	加粗值表示在所有学习方法中最优；
•	星号表示所有方法最优,表示在所有方法中最优（包括传统求解器）；
•	所有问题（除 OP）都是最小化问题；OP 是最大化问题。

总结观察：

•	在大多数问题和规模上，**MDAM（尤其是 bs50 束宽）**达到了最好的效果；
•	相比传统强化学习（如 Nazari et al. 2018）和 AM（Kool et al. 2019），MDAM 的 Obj 值更小、Gap 更低；
•	尽管 MDAM 在时间上略高于贪心方法，但远低于传统优化器（如 Gurobi）在大规模问题上的耗时。

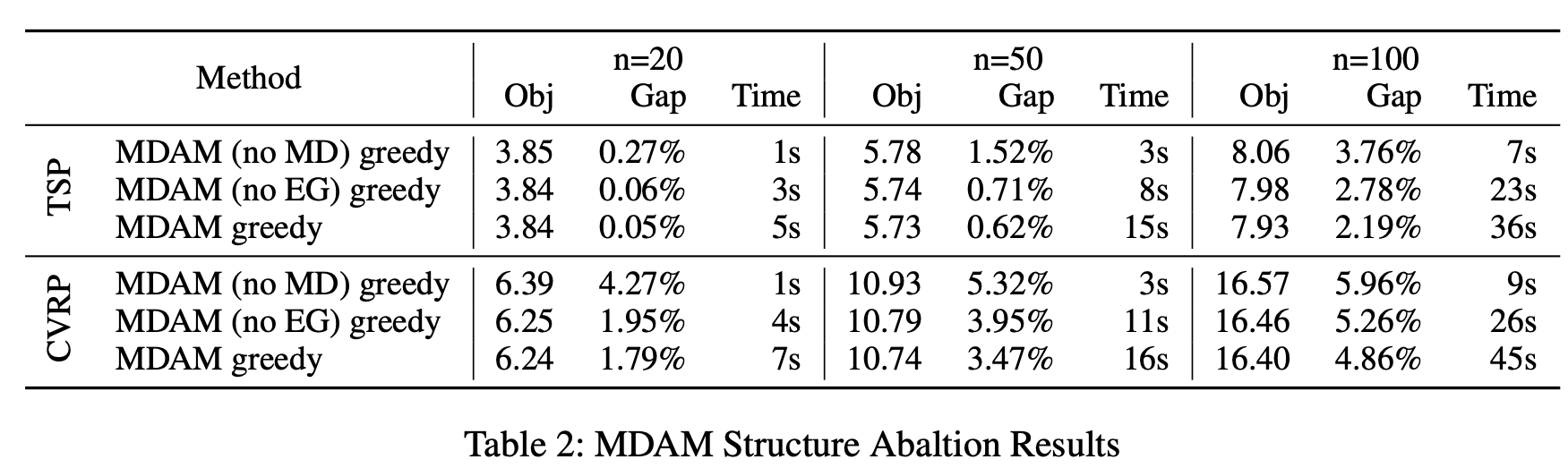
🔬 表 2：MDAM Structure Ablation Results
该表通过 消融实验分析 MDAM 中两个关键组件的重要性：

•	MDAM (no MD)：移除多解码器结构（Multi-Decoder）；
•	MDAM (no EG)：移除 Embedding Glimpse 层；
•	MDAM greedy：完整模型，使用贪心解码策略。

数据展示：
分别在 TSP 和 CVRP 问题上，比较了在 n=20, 50, 100 下三种模型的表现，列包括：

•	Obj：目标函数值；
•	Gap：相对误差；
•	Time：耗时。

总结观察：

•	移除 MD（multi-decoder）会显著增加误差（Gap），说明其对模型性能提升起决定性作用；
•	移除 EG 层会略微增加误差，但开销较小；
•	完整的 MDAM greedy 模型表现最好，验证了两者的协同增强效果。

重点知识总结

核心问题

• 解决组合优化中的路径规划问题（如TSP、CVRP），传统精确算法（如分支定界）计算复杂度高，难以应对大规模问题。
• 现有深度学习方法（如指针网络、Transformer）依赖单一策略生成解，多样性不足，且未充分利用路径构造的递归特性。

创新点

多解码器注意力模型（MDAM）

• 使用一个共享编码器和多个独立解码器，通过KL散度损失鼓励解码器学习差异化策略，提升解多样性。
• 定制化集束搜索策略：为每个解码器分配独立子束，合并相同子问题的解以提升效率。

嵌入凝视层（EG层）

• 在编码器顶层动态屏蔽已访问节点的注意力权重，近似逐步重嵌入，使解码器基于当前有效节点生成更精准的嵌入表示。

训练方法

• 结合REINFORCE算法和贪心滚动基线，通过KL散度损失优化多策略的多样性与单策略质量。

实验结果

• 在TSP、CVRP等六类路径问题上，MDAM显著优于现有深度学习方法（如AM、NeuRewriter），且接近传统求解器（如Concorde、LKH3）的性能。
• 消融实验验证了多解码器结构和EG层的有效性：MD提升解多样性，EG层提升单策略质量。

优势

• 多样性：多解码器生成差异化解，提高找到优质解的概率。
• 效率：EG层通过部分重嵌入减少计算开销，定制集束搜索平衡了解质量与时间成本。
• 通用性：可扩展至带约束或随机性的路径问题（如SDVRP、SPCTSP）。

内容分析

问题驱动

• 指出传统启发式规则依赖人工设计，而现有深度学习方法存在两大局限：
• 单一策略导致解多样性不足；
• 未考虑路径构造的递归特性（已访问节点与后续决策无关）。
• 通过MDAM和EG层同步解决这两个问题，兼具理论创新与工程实用性。

方法设计

MDAM：

• 编码器（Transformer）共享节点嵌入，解码器独立生成策略，通过KL散度损失差异化训练。
• 集束搜索中引入“合并技术”避免重复计算（如TSP中保留相同子问题的更优部分解）。

EG层：

• 在顶层注意力层动态掩码已访问节点，近似逐步更新嵌入，避免全局重编码的高开销。
• 每隔p步执行一次，平衡性能与计算效率。

实验验证

• 对比实验涵盖六类问题，MDAM在贪心解码和束搜索模式下均优于基线模型。
• 消融实验显示MD和EG层的独立贡献（如CVRP100上MDAM比单一解码器提升3.2%）。
• 分析解码器行为：所有解码器均有效贡献，无主导或无效情况。

局限性

• 解码器数量固定，未来可探索动态调整；
• 与传统高度优化的求解器相比，大规模问题上的推理时间仍有差距。

对文章的理解

学术价值

• 提出了一种新的多样性增强机制（MDAM）和嵌入优化技术（EG层），为基于学习的组合优化提供了新思路。
• 通过强化学习框架实现端到端训练，避免了传统方法对问题特定知识的依赖。

工业意义

• 在物流配送等场景中，MDAM能快速生成多样化的高质量解，适应动态约束（如随机需求），优于需要重新优化的传统方法。
• 模型设计兼顾效率与性能，适合实际部署。

启发与展望

• 多策略协同：未来可探索解码器间的交互（如投票机制），而非完全独立决策。
• 扩展性：方法可迁移至其他组合优化问题（如调度、资源分配）。
• 理论解释：进一步研究EG层如何影响嵌入表示的质量，以及多解码器的收敛性。

总结

这篇文章的突破性在于：

1. 模型结构创新：MDAM和EG层首次将解多样性生成与嵌入动态优化结合，显著提升了深度学习在路径规划中的性能上限。
2. 实用价值：在保持传统路径规划理论框架的前提下，提供了更高效的启发式生成工具，尤其适合大规模或动态场景。
3. 研究范式：展示了深度学习在组合优化中的应用潜力——通过数据驱动和模型设计弥补传统方法在灵活性和泛化性上的不足。

局限性：模型仍依赖大量训练数据，且超参数（如解码器数量、EG层步长）需针对问题调整，未来可探索自适应机制。

参考资料

GitHub路径：MDAM 仓库

通过网盘分享的文件：Transformer线路规划论文.pdf
链接: https://pan.baidu.com/s/1wh-IY6I_gXqm4MIyffJ3xg?pwd=ICOF 提取码: ICOF
–来自百度网盘超级会员v6的分享