为什么实用二叉树




一,在有序数组中插入删除数据太慢
1插入或者删除一条数据会移动后面的所有数据
二,在链表中查找数据太慢
2查找只能从头或者尾部一条一条的找
用树解决问题
有没有一种插入和删除像链表那么快,查询可以向有序数组一样查得快那样就好了。
数实现了这些特点,称为了最有意思的数据结构之一
树的术语
如下图

树分平衡树和非平衡树

二叉树的类
public class Tree {
/**
* 跟节点
*/
private Node root;
/**
* 构造方法
*/
public Tree() {
}
/**
* 构造方法
*
* @param root
* 跟节点
*/
public Tree(Node root) {
this.root = root;
}
}
class Node {
/* key */
int key;
/* 值 */
Object value;
/* 左节点 */
Node leftChildNode;
/* 右节点 */
Node rightChildNode;
/**
* 构造方法
*
* @param key
* 关键字
* @param value
* 值
*/
public Node(int key, Object value) {
super();
this.key = key;
this.value = value;
}
}
二叉树插入功能

/**
* 插入节点
*
* @param key
* key
* @param value
* 值
*/
public void insert(int key, Object value) {
Node node = new Node(key, value);
if (this.root == null) {
this.root = node;
} else {
Node currentNode = this.root;
while (true) {
if (key > currentNode.key) {
if (currentNode.rightChildNode == null) {
currentNode.rightChildNode = node;
return;
} else {
currentNode = currentNode.rightChildNode;
}
} else {
if (currentNode.leftChildNode == null) {
currentNode.leftChildNode = node;
return;
} else {
currentNode = currentNode.leftChildNode;
}
}
}
}
}
二叉树的查找功能

/**
* 查找节点
*
* @param key
* @return
*/
public Node find(int key) {
if (this.root != null) {
Node currentNode = this.root;
while (currentNode.key != key) {
if (key > currentNode.key) {
currentNode = currentNode.rightChildNode;
} else {
currentNode = currentNode.leftChildNode;
}
if (currentNode == null) {
return null;
}
}
}
return currentNode ;
}
二叉树的展示功能(中序遍历)
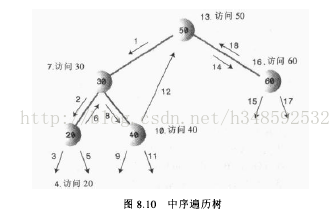
测试
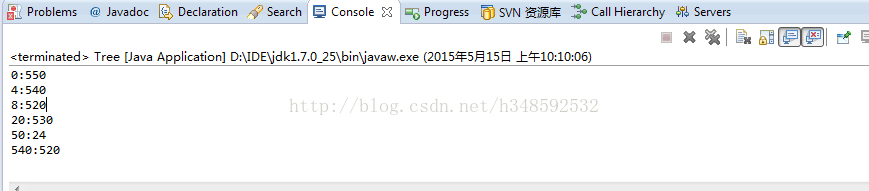
完整代码

private void show(Node node) {
if (node != null) {
this.show(node.leftChildNode);
System.out.println(node.key + ":" + node.value);
this.show(node.rightChildNode);
}
}测试
public static void main(String[] args) {
Node root = new Node(50, 24);
Tree tree = new Tree(root);
tree.insert(20, 530);
tree.insert(540, 520);
tree.insert(4, 540);
tree.insert(0, 550);
tree.insert(8, 520);
tree.show();
}
完整代码
package tree;
/**
* 二叉树
*
* @author JYC506
*
*/
public class Tree {
/**
* 跟节点
*/
private Node root;
/**
* 构造方法
*/
public Tree() {
}
/**
* 构造方法
*
* @param root
* 跟节点
*/
public Tree(Node root) {
this.root = root;
}
/**
* 查找节点
*
* @param key
* @return
*/
public Node find(int key) {
if (this.root != null) {
Node currentNode = this.root;
while (currentNode.key != key) {
if (key > currentNode.key) {
currentNode = currentNode.rightChildNode;
} else {
currentNode = currentNode.leftChildNode;
}
if (currentNode == null) {
return null;
}
}
}
return null;
}
/**
* 插入节点
*
* @param key
* key
* @param value
* 值
*/
public void insert(int key, Object value) {
Node node = new Node(key, value);
if (this.root == null) {
this.root = node;
} else {
Node currentNode = this.root;
while (true) {
if (key > currentNode.key) {
if (currentNode.rightChildNode == null) {
currentNode.rightChildNode = node;
return;
} else {
currentNode = currentNode.rightChildNode;
}
} else {
if (currentNode.leftChildNode == null) {
currentNode.leftChildNode = node;
return;
} else {
currentNode = currentNode.leftChildNode;
}
}
}
}
}
/**
* 展示
*/
public void show() {
this.show(root);
}
/**
* 中序遍历
*
* @param node
*/
private void show(Node node) {
if (node != null) {
this.show(node.leftChildNode);
System.out.println(node.key + ":" + node.value);
this.show(node.rightChildNode);
}
}
public static void main(String[] args) {
Node root = new Node(50, 24);
Tree tree = new Tree(root);
tree.insert(20, 530);
tree.insert(540, 520);
tree.insert(4, 540);
tree.insert(0, 550);
tree.insert(8, 520);
tree.show();
}
}
class Node {
/* key */
int key;
/* 值 */
Object value;
/* 左节点 */
Node leftChildNode;
/* 右节点 */
Node rightChildNode;
/**
* 构造方法
*
* @param key
* 关键字
* @param value
* 值
*/
public Node(int key, Object value) {
super();
this.key = key;
this.value = value;
}
}





















 666
666

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








