T1:最小比例(ratio)
Description
图中共有N个点的完全图,每条边都有权值,每个点也有权值。要求选出M个点和M-1条边,构成一棵树,使得:
即所有边的权值与所有点的权值之和的比率最小。
给定N和M,以及N个点的权值,和所有的边权,要求M个点的最小比率生成树。
Input
第一行包含两个整数N和M(2<=N<=15,2<=M<=N),表示点数和生成树的点数。
接下来一行N个整数,表示N个点的边权。
最后N行,每行N列,表示完全图中的边权。所有点权和边权都在[1,100]之间。
Output
输出最小比率生成树的M个点。当答案出现多种时,要求输出的第一个点的编号尽量小,第一个相同,则第二个点的编号尽量小,依次类推,中间用空格分开。编号从1开始。
Sample Input
输入1:3 2 30 20 10 0 6 2 6 0 3 2 3 0输入2:
2 2 1 1 0 2 2 0
Sample Output
输出1:1 3输出2:
1 2
Data Constraint
对于30%数据,N<=5。
简要思路:一开始看这题,还以为是涉及到分数规划的最优比例生成树desert king,后面发现这题是求给定数量的点(不一定包括所有点)的生成树(假生成树),一开始觉得很难对付,再瞄一眼数据范围,N最大才15,那还犹豫啥,暴力枚举啊,只要枚举时用状压,再注意一下细节即可。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define inf 0x3f3f3f3f
using namespace std;
const int N = 20;
int n , m , sta;
int vis[N] , flag[N] , val[N] , map[N][N] , ans[N] , d[N];
int sume , sumn;
double minn;
struct node{
int pos;
int dis;
friend bool operator < ( node a , node b ) {
return a.dis > b.dis;
}
};
priority_queue <node> q;
inline void read( int & res ) {
res = 0;
int pd = 1;
char a = getchar();
while ( a < '0' || a > '9' ) {
if ( a == '-' ) {
pd = -pd;
}
a = getchar();
}
while ( a >= '0' && a <= '9' ) {
res = ( res << 1 ) + ( res << 3 ) + ( a - '0' );
a = getchar();
}
res *= pd;
return;
}
inline int cunt( int s ) {
int res = 0;
for ( int i = 0 ; i <= n - 1 ; ++i ) {
if ( s & ( 1 << i ) ) {
++res;
}
}
return res;
}
inline void prim() {
for ( int i = 1 ; i <= n ; ++i ) {
d[i] = inf;
vis[i] = 0;
}
d[sta] = 0;
node tt;
tt.dis = 0;
tt.pos = sta;
q.push(tt);
while ( !q.empty() ) {
node te = q.top();
int cur = te.pos;
q.pop();
if ( vis[cur] ) {
continue;
}
vis[cur] = 1;
sume += d[cur];
for ( int i = 1 ; i <= n ; ++i ) {
if ( !vis[i] && flag[i] && i != cur && d[i] > map[i][cur] ) {
d[i] = map[i][cur];
node tem;
tem.dis = d[i];
tem.pos = i;
q.push(tem);
}
}
}
double res = (double)(sume) / (double)(sumn);
bool fl = false;
if ( res < minn ) {
minn = res;
int cnt = 0;
for ( int i = 1 ; i <= n ; ++i ) {
if ( flag[i] ) {
ans[++cnt] = i;
}
}
} else if ( res == minn ) {
int cnt = 0;
for ( int i = 1 ; i <= n ; ++i ) {
if ( flag[i] ) {
cnt++;
if ( ans[cnt] < i ) {
break;
} else if ( ans[cnt] > i ) {
fl = true;
break;
}
/*不要写成
if ( ans[++cnt] < i ) {
break;
} else if ( ans[++cnt] > i ) {
fl = true;
break;
}
我就是这样才拿六十分的!*/
}
}
if (fl) {
cnt = 0;
for ( int i = 1 ; i <= n ; ++i ) {
if ( flag[i] ) {
ans[++cnt] = i;
}
}
}
}
return;
}
int main () {
//freopen( "ratio.in" , "r" , stdin);
//freopen( "ratio.out" , "w" , stdout );
read(n);
read(m);
minn = 1000000000.0;
for ( int i = 1 ; i <= n ; ++i ) {
read(val[i]);
}
for ( int i = 1 ; i <= n ; ++i ) {
for ( int j = 1 ; j <= n ; ++j ) {
read(map[i][j]);
}
}
for ( int i = 1 ; i <= ( 1 << n ) - 1 ; ++i ) {
if ( cunt(i) != m ) {
continue;
}
sume = 0;
sumn = 0;
for ( int j = 0 ; j <= n - 1 ; ++j ) {
if ( i & ( 1 << j ) ) {
flag[j + 1] = 1;
sta = j + 1;
sumn += val[j + 1];
} else {
flag[j + 1] = 0;
}
}
prim();
}
printf("%d",ans[1]);
for ( int i = 2 ; i <= m ; ++i ) {
printf(" %d",ans[i]);
}
return 0;
}
T2:软件公司(company)
Description
一家软件开发公司有两个项目,并且这两个项目都由相同数量的m个子项目组成,对于同一个项目,每个子项目都是相互独立且工作量相当的,并且一个项目必须在m个子项目全部完成后才算整个项目完成。
这家公司有n名程序员分配给这两个项目,每个子项目必须由一名程序员一次完成,多名程序员可以同时做同一个项目中的不同子项目。
求最小的时间T使得公司能在T时间内完成两个项目。
Input
第一行两个正整数n,m(1<=n<=100,1<=m<=100)。
接下来n行,每行包含两个整数,x和y。分别表示每个程序员完成第一个项目的子程序的时间,和完成第二个项目子程序的时间。每个子程序耗时也不超过100。
Output
输出最小的时间T。
Sample Input
3 20 1 1 2 4 1 6
Sample Output
18
Hint
【样例解释】
第一个人做18个2项目,耗时18;第二个人做2个1项目,2个2项目耗时12;第三个人做18个1项目,耗时18。
Data Constraint
对于30%的数据,n<=30.
对于60%的数据,n<=60.
简要思路:这题如果不往二分和DP上想是很难想出正解的,不过,暴力却非常好打。
//暴力代码,稳拿部分分
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int n , m , ans;
int x[105] , y[105];
inline void read( int & res ) {
res = 0;
int pd = 1;
char a = getchar();
while ( a < '0' || a > '9' ) {
if ( a == '-' ) {
pd = -pd;
}
a = getchar();
}
while ( a >= '0' && a <= '9' ) {
res = ( res << 1 ) + ( res << 3 ) + ( a - '0' );
a = getchar();
}
res *= pd;
return;
}
inline int max( int a , int b ) {
return a > b ? a : b;
}
inline int min( int a , int b ) {
return a < b ? a : b;
}
inline void dfs( int depth , int sum , int m1 , int m2 ) {
if ( depth == n + 1 ) {
ans = min( ans , sum );
return;
}
if ( depth == n ) {
dfs( depth + 1 , max( sum , m1 * x[n] + m2 * y[n] ) , 0 , 0 );
return;
}
for ( int i = 0 ; i <= m1 ; ++i ) {
if ( i > m1 ) {
return;
}
for ( int j = 0 ; j <= m2 ; ++j ) {
if ( j > m2 ) {
break;
}
dfs( depth + 1 , max( sum , x[depth] * i + y[depth] * j ) , m1 - i , m2 - j );
}
}
}
int main () {
//freopen( "company.in" , "r" , stdin );
//freopen( "company.out" , "w" , stdout );
read(n);
read(m);
for ( int i = 1 ; i <= n ; ++i ) {
read(x[i]);
read(y[i]);
}
ans = 0x7f7f7f7f;
dfs( 1 , 0 , m , m );
printf("%d",ans);
return 0;
}
好了,接下来就该认真讲正解了,我们先用DP方程
f
[
i
]
[
j
]
[
k
]
f[i][j][k]
f[i][j][k]表示前
i
i
i个人,完成了
j
j
j个1项目,
k
k
k个2项目的用时,转移也不难,就是
f
[
i
]
[
j
]
[
k
]
=
m
a
x
f
[
i
]
[
j
−
s
]
[
k
−
t
]
,
s
∗
A
[
i
]
+
t
∗
B
[
i
]
f[i][j][k] = max{f[i][j - s][k - t],s * A[i] + t * B[i]}
f[i][j][k]=maxf[i][j−s][k−t],s∗A[i]+t∗B[i],不过算一下时间复杂度,为
O
(
n
∗
m
4
)
O(n * m ^ 4)
O(n∗m4),只能拿30分(还不如暴力呢 )。
那就优化吧,分析样例不难发现,样例的答案之所以为18,是因为耗时为17时不存在可行方案,而耗时大于等于18时一定会有一个可行方案(当然,不要太大)。由此可知答案为线性的,可以考虑二分!
二分答案后,最大值已知,当得知某个人完成1项目的数目时,可用贪心推出完成2项目的数目,此时,我们用
f
[
i
]
[
j
]
f[i][j]
f[i][j]表示前
i
i
i个人,共完成
j
j
j个1项目,2项目最多能完成的个数,转移为
f
[
i
]
[
j
]
=
m
a
x
f
[
i
]
[
j
]
,
f
[
i
−
1
]
[
j
−
k
]
+
(
a
n
s
−
A
[
i
]
)
B
[
i
]
f[i][j] = max{f[i][j] , f[i - 1][j - k] + {( ans - A[i] ) \over B[i]}}
f[i][j]=maxf[i][j],f[i−1][j−k]+B[i](ans−A[i]),这样,时间复杂度为
O
(
n
∗
m
2
∗
l
o
g
(
二
分
上
界
)
)
O(n * m ^ 2 * log(二分上界))
O(n∗m2∗log(二分上界)),可以愉快的通过所有的数据。
#include <iostream>
#include <cstdio>
#include <cstring>
#define inf 0x3f3f3f3f
using namespace std;
int n , m , ans;
int x[105] , y[105];
int f[105][105];//表示完成j个A的子任务时最多完成的B的子任务数
inline void read( int & res ) {
res = 0;
int pd = 1;
char a = getchar();
while ( a < '0' || a > '9' ) {
if ( a == '-' ) {
pd = -pd;
}
a = getchar();
}
while ( a >= '0' && a <= '9' ) {
res = ( res << 1 ) + ( res << 3 ) + ( a - '0' );
a = getchar();
}
res *= pd;
return;
}
inline int max( int a , int b ) {
return a > b ? a : b;
}
inline int min( int a , int b ) {
return a < b ? a : b;
}
int main () {
//freopen( "company.in" , "r" , stdin );
//freopen( "company.out" , "w" , stdout );
read(n);
read(m);
for ( int i = 1 ; i <= n ; ++i ) {
read(x[i]);
read(y[i]);
}
int l = 0 , r = 1000;
while ( l < r ) {
int mid = ( l + r ) >> 1;
for ( int i = 0 ; i <= n ; ++i ) {
for ( int j = 0 ; j <= m ; ++j ) {
f[i][j] = -inf;
}
}
f[0][0] = 0;
for ( int i = 1 ; i <= n ; ++i ) {
for ( int j = 0 ; j <= m ; ++j ) {
for ( int k = 0 ; k <= j ; ++k ) {
if ( x[i] * k > mid ) {
break;
}
f[i][j] = max( f[i][j] , f[i - 1][j - k] + ( mid - x[i] * k ) / y[i] );
}
}
}
if ( f[n][m] >= m ) {
r = mid;
} else {
l = mid + 1;
}
}
printf("%d",r);
return 0;
}
最后,贴一份JZ的老师的总结:
这是一道2004年ACM亚洲区德黑兰站的预赛题。可能比较老的题目了。拿出这个题目想和大家一起探讨一下近几年NOIP题中出现的一个较热门的思想,二分答案!10年的关押罪犯,11年的聪明的质监员,12年的借教室,都有二分答案的方法。而且都是区分水平的关键题。
我们可以总结一下,当碰到所求问题是最小值最大,最大值最小,答案存在线性的临界点的时候,我们都可以二分这个答案,然后根据二分的值设计判断答案可行性的函数。
二分的重要性可见一斑啊!
T3:空间航行(warp)
Description
你是一艘战列巡洋舰的引擎操作人员,这艘船的船员在空间中侦测到了一些无法辨识的异常信号。你的指挥官给你下达了命令,让你制定航线,驾驶战列巡洋舰到达那里。
船上老旧的曲速引擎的速度是0.1AU/s。然而,在太空中分布着许多殖民星域,这些星域可以被看成一个球。在星域的内部,你可以在任何地方任意次跳跃到星域内部的任意一个点,不花费任何时间。
你希望算出到达终点的最短时间。
Input
输入包含多组测试数据。
对于每一组数据,第一行包含一个正整数n,表示殖民星域的数量。
接下来n 行,第i 行包含四个整数Xi,Yi,Zi,Ri,表示第i个星域的中心坐标为(Xi, Yi,Zi),星域的半径是Ri。
接下来两行,第一行包含值Xa,Ya,Za,告诉你当前坐标为(Xa, Ya,Za)。
第二行包含值Xo,Yo,Zo,告诉你目的地坐标为(Xo, Yo,Zo)。
输入以一行单独的-1 结尾。所有坐标的单位都是天文单位(AU)。
Output
对于每一组输入数据,输出一行表示从目前的位置到达指定目的地的最短时间,取整到最近整数。输入保证取整是明确的。
Sample Input
1 20 20 20 1 0 0 0 0 0 10 1 5 0 0 4 0 0 0 10 0 0 -1
Sample Output
100 20
Data Constraint
每个输入文件至多包含10 个测试数据。
对于10% 的数据,n = 0。
对于30% 的数据,0<=n<=10。
对于100% 的数据,0<=n<=100,所有坐标的绝对值<=10000 ,半径r<=10000。
你可以认为,你所在的星区的大小为无限大。
简要思路:这题看上去没什么思路,实际上只要通过一定的手段建图并且跑Dij或floyrd即可(数据小)。
 观察图片,假若最短路经过一个殖民星域,则从A点到B点经过圆C的最短路一定是A与C的连线以及B与C的连线。只要熟悉圆的性质,不难看出,
∣
A
D
∣
<
∣
A
I
∣
|AD| < |AI|
∣AD∣<∣AI∣,这一点很容易推广到三维,上述结论成立。
观察图片,假若最短路经过一个殖民星域,则从A点到B点经过圆C的最短路一定是A与C的连线以及B与C的连线。只要熟悉圆的性质,不难看出,
∣
A
D
∣
<
∣
A
I
∣
|AD| < |AI|
∣AD∣<∣AI∣,这一点很容易推广到三维,上述结论成立。
把起点,终点当做半径为零的点,两圆距离为圆心距离减去两圆半径,建成一个图后跑最短路。
同时要注意特判两圆相交的情况,将它们之间的距离设为零即可。
最后补充一下,注意精度。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <cmath>
using namespace std;
int n;
struct no{
int x;
int y;
int z;
int r;
}num[103];
int vis[103];
double d[103];
struct node{
double dis;
int pos;
friend bool operator < ( node a , node b ) {
return a.dis > b.dis;
}
};
priority_queue <node> q;
inline void read( int & res ) {
res = 0;
int pd = 1;
char a = getchar();
while ( a < '0' || a > '9' ) {
if ( a == '-' ) {
pd = -pd;
}
a = getchar();
}
while ( a >= '0' && a <= '9' ) {
res = ( res << 1 ) + ( res << 3 ) + ( a - '0' );
a = getchar();
}
res *= pd;
return;
}
inline double cnt( int i , int j ) {
double res = sqrt( (double)( num[i].x - num[j].x ) * (double)( num[i].x - num[j].x ) + (double)( num[i].y - num[j].y ) * (double)( num[i].y - num[j].y ) + (double)( num[i].z - num[j].z ) * (double)( num[i].z - num[j].z ) );
res -= (double)(num[i].r);
res -= (double)(num[j].r);
if( res < 0 ) {
return 0;
}
return res;
}
inline void dij() {
node tt;
tt.dis = 0;
tt.pos = 1;
q.push(tt);
while ( !q.empty() ) {
node te;
te = q.top();
q.pop();
int cur = te.pos;
if ( vis[cur] ) {
continue;
}
vis[cur] = 1;
for ( int i = 1 ; i <= n + 2 ; ++i ) {
if ( !vis[i] ) {
double res = cnt( cur , i );
if ( d[cur] + res < d[i] ) {
d[i] = d[cur] + res;
node tem;
tem.pos = i;
tem.dis = d[i];
q.push(tem);
}
}
}
}
return;
}
int main () {
//freopen( "warp.in" , "r" , stdin );
//freopen( "warp.out" , "w" , stdout );
while ( scanf("%d",&n) != EOF && ~n ) {
memset( vis , 0 , sizeof(vis) );
for ( int i = 2 ; i <= n + 1 ; ++i ) {
read(num[i].x);
read(num[i].y);
read(num[i].z);
read(num[i].r);
d[i] = 1000000000.0;//据说double用memset赋初值容易出问题
}
num[1].r = 0;
d[1] = 0;
read(num[1].x);
read(num[1].y);
read(num[1].z);
num[n + 2].r = 0;
d[n + 2] = 1000000000.0;
read(num[n + 2].x);
read(num[n + 2].y);
read(num[n + 2].z);
dij();
d[n + 2] *= 10.0;
printf("%.lf\n",d[n + 2]);
}
return 0;
}
T4:摧毁巴士站(bus)
Description
被和谐了
Input
第一行包含三个整数n,m,k (2<n<=50,0<m<=4000,0<k<1000)。
接下来m行,每行2个整数s和f,表示从站s到站f有一条路。
Output
输出最少需要**的巴士站数目。
Sample Input
5 7 3 1 3 3 4 4 5 1 2 2 5 1 4 4 5
Sample Output
2
Data Constraint
30%的数据N<=15。
简要思路:据老师说这道题可以用网络流,不过,老师后面又加了一句:就看它的数据范围,这题用网络流真是用牛刀杀鸡 。通过观察它的数据范围,不难发现,暴力枚举是可行的,但是盲目的枚举会超时。我们可以用SPFA求当前最短路,将当前最短路上的点记录下来,可用
f
a
[
x
]
fa[x]
fa[x]表示最短路上的节点
x
x
x在最短路上的父亲节点的方法记录最短路(好吧,这就是绕口令 )。若最短路符合要求,得出答案;若不符合要求,暴力枚举删除最短路上的点,接着进行下一次求最短路和删点,因为当前选择不一定最优,所以要递归处理,最优性剪枝什么的也不用说了。
递归过程如下(JZ文档里的):
- 寻找起点到终点的最短路径,如果最短路径长度超过k,则表示已找到一种删点方案。记录该方案下的删点数目,回溯再找出下一种方案;否则进入下一步。
- 枚举最短路径中的除1号点和n号点外的某一个点,将其删除。
- 回到1递归继续搜索。
最后用感性的方法证明暴搜的可行性,在搜索前期,我们搜到的最短路不长,枚举的点数少,到了后期,如果当前找到的最短路径很长,虽然在这一层我们需要枚举很多个点进行删除,但也说明起点到终点的距离已经很长了,我们离答案已经很接近了。
再提一点,本题是有向图,我就被这坑了一个多小时 。
#include <iostream>
#include <cstdio>
#include <cstring>
#define inf 0x3f3f3f3f
using namespace std;
int n , m , k , bcnt , ans;
int b[51][51];
int del[51] , q[105] , fa[51] , vis[51] , d[51];
bool flag , cho;
inline void read( int & res ) {
res = 0;
int pd = 1;
char a = getchar();
while ( a < '0' || a > '9' ) {
if ( a == '-' ) {
pd = -pd;
}
a = getchar();
}
while ( a >= '0' && a <= '9' ) {
res = ( res << 1 ) + ( res << 3 ) + ( a - '0' );
a = getchar();
}
res *= pd;
return;
}
inline void spfa() {
int l = 1 , r = 1;
memset( d , 0x3f , sizeof(d) );
memset( vis , 0 , sizeof(vis) );
q[1] = 1;
d[1] = 0;
vis[1] = 1;
while ( l <= r ) {
int cur = q[l];
vis[cur] = 0;
for ( int i = 1 ; i <= n ; ++i ) {
if ( b[cur][i] > 0 && !del[i] && d[i] > d[cur] + 1 ) {
d[i] = d[cur] + 1;
fa[i] = cur;
if ( !vis[i] ) {
vis[i] = 1;
q[++r] = i;
}
}
}
l++;
}
return;
}
void find( int depth ) {
if ( depth > ans ) {
return;
}
spfa();
if ( d[n] > k ) {
if ( depth < ans ) {
ans = depth;
return;
}
}
int chosen[51];
int cnt = 0;
int tem = n;
while ( tem ) {
if ( tem != 1 && tem != n ) {
chosen[++cnt] = tem;
}
tem = fa[tem];
}
for ( int i = 1 ; i <= cnt ; ++i ) {
del[chosen[i]] = 1;
find( depth + 1 );
del[chosen[i]] = 0;
}
return;
}
int main () {
//freopen( "bus.in" , "r" , stdin );
//freopen( "bus.out" , "w" , stdout );
read(n);
read(m);
read(k);
int x , y;
for ( int i = 1 ; i <= m ; ++i ) {
read(x);
read(y);
b[x][y]= 1;
}
fa[1] = 0;
ans = inf;
find(0);
printf("%d",ans);
return 0;
}
现在贴上老师的感悟作结吧:
这个题目同样是ACM08年北京站的题目,现场赛25次提交,4队通过,应该是难题了。其实,对OIer来说,搜索的技巧更是需要不断通过难题来积累的。记得以前常问不少大神,某某题是怎么做的,无数次得到的回答是:暴搜!当然,此暴搜肯定是经过了许多的优化,而这些优化在高手日积月累的搜索技巧面前就是家常便饭了。在OI中,同样的题目,都采用搜索,有些就只能拿基本分,而有些就可以拿下大部分,甚至AC,这种情况很常见。搜索技巧在很多时候也成了区分OI选手水平的重要标志。要提高也只能通过不断的做题,了解不同类型题目的搜索剪枝技巧,还有就是尝试一些IDDFS,A*等不同的搜索方式。水平有限,也希望大神们可以总结一些好的搜索攻略。








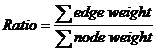













 184
184











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








