gauss 函数

高斯滤波（高斯平滑）是图像处理，计算机视觉里面最常见的操作。平时，我们都是用matlab或者opencv的函数调用：imfilter或者cvSmooth，并不关心底层的实现。然而当开发者要实做高斯滤波的时候，往往就会很迷惘，往往会被以下几个问题困扰：

1. 给定sigma，即标准偏差，怎么确定离散化后滤波器的窗口大小？
2. 给定窗口大小，怎么计算高斯核的sigma，即标准方差？
3. 怎么实现可分离滤波器？

我在google上搜了一下，还真没几个人把实现的细节讲清楚了。这里，我尝试结合三份源码，做个小小的总结。

三份源码分别是：

1. opencv 中的cvfilter.cpp
2. autopano-sift-c 中的GaussianConvolution.c
3. GIMP 中的blur-gauss.c和unsharp-mask.c

在图像处理中，高斯滤波一般有两种实现方式，一是用离散化窗口滑窗卷积，另一种通过傅里叶变换。最常见的就是第一种滑窗实现，只有当离散化的窗口非 常大，用滑窗计算量非常大（即使用可分离滤波器的实现）的情况下，可能会考虑基于傅里叶变化的实现方法。这里我们只讨论第一种方法。

二维高斯函数的形式是这样的：

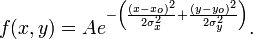
有着如下的形状，形状很激凸，怎么会叫高斯平滑呢，分明是高斯激凸嘛：

基本上，离散化的主旨就是保留高斯函数中心能量最集中的中间部分，忽略四周能量很小的平坦区域。这只是个很感性的描述，具体实现起来，就会出现千奇百怪的版本。下面结合三份源码，看看现实世界里的高斯平滑到底长的什么样子。

首先是第一个问题：给定sigma，怎么计算窗口大小？

直接上opencv的源码，在cvFilter函数中：

param1 = cvRound(sigma1*(depth == CV_8U ? 3 : 4)*2 + 1)|1;

opencv认为半径为3*sigma的窗口就是高斯函数能量最集中的区域。（为什么在图像深度不是8U的时候，使用4*sigma半径的窗口就不得而知了，有高人指点一下？）

autopan0-sift-c是图像拼接软件hugin里面的sift实现，在实现DoG的时候需要做不同尺度的高斯平滑，实现如下，在GaussianConvolution_new1函数中：

dim = 1 + 2 * ((int) (3.0 * sigma));

可见autopano也是实现的3*sigma半径的窗口。

在GIMP里，实现比较奇特，在blur_gauss.c的make_rle_curve函数里面，

const gdouble sigma2 = 2 * sigma * sigma;
const gdouble l = sqrt (-sigma2 * log (1.0 / 255.0));
int n = ceil (l) * 2;
if ((n % 2) == 0)
n += 1;

我是没看懂那个 log (1.0 / 255.0)是干嘛的。。。惭愧。效果来看，这个实现的窗口半径是约等于2.2*sigma。

然后是第二个问题：给定窗口大小，怎么计算sigma？

opencv的实现，在cvFilter.cpp的init_gaussian_kernel函数中：

sigmaX = sigma > 0 ? sigma : (n/2 – 1)*0.3 + 0.8;

再次不可解。。。乘以0.3还可以接受，加上0.8是为嘛啊？

autopano没有实现这个特性。

GIMP的实现：

/* we want to generate a matrix that goes out a certain radius
* from the center, so we have to go out ceil(rad-0.5) pixels,
* inlcuding the center pixel. Of course, that’s only in one direction,
* so we have to go the same amount in the other direction, but not count
* the center pixel again. So we double the previous result and subtract
* one.
* The radius parameter that is passed to this function is used as
* the standard deviation, and the radius of effect is the
* standard deviation * 2. It’s a little confusing.
*/
radius = fabs (radius) + 1.0;

std_dev = radius;
radius = std_dev * 2;
/* go out ‘radius’ in each direction */
matrix_length = 2 * ceil (radius – 0.5) + 1;

注释讲的很清楚了，基本上就是认为sigma应该等于窗口半径的一半。

看完这三分源码，结论就是，关于sigma和半径，你爱怎么算就怎么算吧，差不多就行。。。（额。。费了半天劲，就得到这么一句废话啊）。

第三个问题是可分离滤波器：

由于高斯函数可以写成可分离的形式，因此可以采用可分离滤波器实现来加速。所谓的可分离滤波器，就是可以把多维的卷积化成多个一维卷积。具体到二维 的高斯滤波，就是指先对行做一维卷积，再对列做一维卷积。这样就可以将计算复杂度从O(M*M*N*N)降到O(2*M*M*N)，M，N分别是图像和滤 波器的窗口大小。问题是实现时候怎么计算一维的卷积核呢？

其实很简单，按照前面计算出来的窗口大小，计算所有离散点上一维高斯函数的权值，最后别忘了将权值之和归一化到1.
有码有真相，来自opencv：

for( i = 0; i <= n/2; i++ )
{
double t = fixed_kernel ? (double)fixed_kernel[i] : exp(scale2X*i*i);
if( type == CV_32FC1 )
{
cf[(n/2+i)*step] = (float)t;
sum += cf[(n/2+i)*step]*2;
}
else
{
cd[(n/2+i)*step] = t;
sum += cd[(n/2+i)*step]*2;
}
}

sum = 1./sum;
for( i = 0; i <= n/2; i++ )
{
if( type == CV_32FC1 )
cf[(n/2+i)*step] = cf[(n/2-i)*step] = (float)(cf[(n/2+i)*step]*sum);
else
cd[(n/2+i)*step] = cd[(n/2-i)*step] = cd[(n/2+i)*step]*sum;
}

终于写完了，希望对各位有所帮助。不对之处请指正哈。