算法通关村第十八关——回溯是怎么回事（青铜）

最新推荐文章于 2024-05-11 14:30:05 发布
最新推荐文章于 2024-05-11 14:30:05 发布
阅读量150 收藏
点赞数
分类专栏： 数据结构 算法 文章标签： 算法 java 数据结构 笔记
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/hai_helloyou/article/details/132673530
版权

算法通关村第十八关——回溯是怎么回事（青铜）

前言

回溯算法是一种解决问题的常见方法，特别适用于在给定约束条件下搜索所有可能的解空间。它通过不断地尝试和撤销选择来寻找问题的解，因此也被称为"试错法"。本文将详细介绍回溯算法，并通过图解和具体例子讲解其原理和应用。

回溯可以视为递归的拓展，很多思想和解法都与递归密切相关，在很多材料中都将回溯都与递归同时解释，例如本章2.1的路径问题就可以使用递归和回溯两种方法来解决。因此学习回溯时，我们对比递归来分析其特征会理解更深刻。

关于递归和回溯的区别，我们设想一个场景，某猛男想脱单，现在有两种策略：

  1. 递归策略：先与意中人制造偶遇，然后了解人家的情况，然后约人家吃饭，有好感之后尝试拉人家的手，没有拒绝就表白。

  2. 回溯策略：先统计周围所有的单身女孩，然后一个一个表白， 被拒绝就说“我喝醉了”，然后就当啥也没发生，继续找下一个。

  • 回溯最大的好处是有非常明确的模板，所有的回溯都是一个大框架，因此透彻理解回溯的框架是解决一切回溯问题的基础。第一章我们只干一件事，那就是分析这个框架。

  • 回溯不是万能的，而且能解决的问题也是非常明确的，例如组合、分割、子集、排列，棋盘等等，不过这些问题具体处理时又有很多不同，本章我们梳理了多个最为热门的问题来解释，请同学们认真对待。

  • 回溯可以理解为递归的拓展，而代码结构又特别像深度遍历N叉树，因此只要知道递归，理解回溯并不难，难在很多人不理解为什么在递归语句之后要有个“撤销”的操作。

  • 回溯最让人激动的是有非常清晰的解题模板，如下所示，大部分的回溯代码框架都是这个样子，具体为什么这样子我们后面再解释。

void backtracking(参数) {
	if (终止条件) {
        存放结果;
        return;
	}
	for (选择本层集合中元素（画成树，就是树节点孩子的大小）){
        处理节点;
        backtracking();
        回溯，撤销处理结果;
	}
}

1. 从N叉树说起

1.1 N叉树的定义和特点

N叉树是一种特殊的树结构，每个节点最多可以有N个子节点。与二叉树不同，N叉树可以支持更多的分支情况，这使得回溯算法在处理多个选择时更加灵活。

二叉树

class TreeNode{
	int val;
	TreeNode left;
	TreeNode right;
}

N叉树

class TreeNode{
	int val;
	List<TreeNode> nodes;
}

遍历代码：

public static void treeDFS(TreeNode root) {
	//递归必须要有终止条件
	if (root == null){
		return;
	}
	// 处理节点
	System.out.println(root.val);
	//通过循环，分别遍历N个子树
	for (int i = 1; i <= nodes.length; i++) {
		treeDFS("第i个子节点");
	}
}

到这里，你有没有发现和上面说的回溯的模板非常像了？是的！非常像！既然很像，那说明两者一定存在某种关系。其他暂时不管，现在你只要先明白回溯的大框架就是遍历N叉树就行了。

1.2 N叉树的遍历方式

N叉树可以通过深度优先搜索（DFS）或广度优先搜索（BFS）进行遍历。其中，DFS更适合回溯算法的实现，因为它能够深入到每个可能的选择路径。

N叉树的深度优先搜索（DFS）遍历是使用递归方式实现的。下面是使用Java代码实现N叉树的DFS遍历：

class Node {
    int val;
    List<Node> children;

    public Node(int val) {
        this.val = val;
        this.children = new ArrayList<>();
    }
}

public void dfs(Node root) {
    if (root == null) return;
    
    System.out.println(root.val); // 先访问当前节点

    for (Node child : root.children) {
        dfs(child); // 递归地访问子节点
    }
}

在上述代码中，我们定义了一个Node类，用于表示N叉树的节点。每个节点包含一个值val和子节点列表children。dfs()函数是深度优先搜索的入口函数。

在dfs()函数中，首先输出当前节点的值。然后使用循环遍历当前节点的所有子节点，并对每个子节点递归调用dfs()函数，以便深入到每个可能的选择路径。

通过以上代码，我们可以对N叉树进行深度优先搜索遍历，获得其所有节点的值。

1.3 N叉树在回溯算法中的应用

N叉树在回溯算法中有广泛的应用，特别是在寻找问题的解空间时。每个节点代表一个选择，通过不断向下递归，我们可以穷尽所有的选择路径，从而找到满足约束条件的解。

以下是一个示例，演示了如何使用N叉树和回溯算法来解决组合问题：

public List<List<Integer>> combine(int n, int k) {
    List<List<Integer>> res = new ArrayList<>();
    if (k <= 0 || n < k) return res;

    List<Integer> path = new ArrayList<>();
    dfs(n, k, 1, path, res);
    
    return res;
}

private void dfs(int n, int k, int start, List<Integer> path, List<List<Integer>> res) {
    if (path.size() == k) {
        res.add(new ArrayList<>(path));
        return;
    }

    for (int i = start; i <= n; i++) {
        path.add(i); // 选择当前数字
        dfs(n, k, i + 1, path, res); // 递归处理下一个数字
        path.remove(path.size() - 1); // 撤销选择，回溯到上一层
    }
}

在上述代码中，我们使用回溯算法解决了组合问题。combine()函数接收两个参数：n表示数字的范围为1到n，k表示每个组合的元素个数。函数返回一个包含所有可能组合的列表。

在dfs()函数中，首先判断当前组合的长度是否达到目标值k，如果是，则将当前组合加入结果集。然后通过循环遍历剩余的数字，并对每个数字进行选择、递归和撤销操作。选择当前数字后，递归处理下一个数字；当递归返回后，撤销当前选择，回溯到上一层。

通过以上代码，我们可以找到满足条件的所有组合，并得到最终结果列表。这个示例展示了N叉树和回溯算法在解决实际问题时的应用。

2. 为什么有的问题暴力搜索也不行

2.1 暴力搜索的局限性

暴力搜索是一种简单直接的方法，通过穷举所有可能的解来寻找问题的解。然而，对于某些复杂的问题，暴力搜索往往会产生指数级别的时间复杂度，导致无法在合理时间内找到解。

我们说回溯主要解决暴力枚举也解决不了的问题，什么问题这么神奇，暴力都搞不定？

看个例子：

LeetCode77 ：给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。例如，输入n=4，k=2，则输出：

[[2,4], [3,4], [2,3], [1,2], [1,3], [1,4]]

首先明确这个题是什么意思，如果n=4，k=2，那就是从4个数中选择2个，问你最后能选出多少组数据。

这个是高中数学中的一个内容，过程大致这样：如果n=4，那就是所有的数字为{1,2,3,4}

  1. 先取一个1，则有[1,2]，[1,3]，[1,4]三种可能。

  2. 然后取一个2，因为1已经取过了，不再取，则有[2,3]，[2,4]两种可能。

  3. 再取一个3，因为1和2都取过了，不再取，则有[3,4]一种可能。

  4. 再取4，因为1，2，3都已经取过了，所以直接返回null。

  5. 所以最终结果就是[1,2]，[1,3]，[1,4]，[2,3]，[2,4]，[3,4]。

这就是我们思考该问题的基本过程，写成代码也很容易，双层循环轻松搞定：

for (int i = 1; i <= n; i++) {
    for (int j = i + 1; j <= n; j++) {
    System.out.println(i + " " + j);
    }
}

假如n和k都变大，比如n是200，k是3呢？也可以，三层循环基本搞定：

for (int i = 1; i <= n; i++) {
    for (int j = i + 1; j <= n; j++) {
        for (int u = j + 1; u <= n; n++) {
        	System.out.println(i + " " + j + " " + u);
        }
    }
}

如何这里的K是5呢？甚至是50呢？你需要套多少层循环？甚至告诉你K就是一个未知的正整数k，你怎么写循环呢？这时候已经无能为例了？所以暴力搜索就不行了。

这就是组合类型问题，除此之外子集、排列、切割、棋盘等方面都有类似的问题，因此我们要找更好的方式。

3. 回溯=递归+局部枚举+放下前任

3.1 回溯算法的基本思想和原理

回溯算法的基本思想是通过递归去尝试所有可能的选择，并在每次递归中进行剪枝操作，从而避免无效的搜索路径。它借助"局部枚举"的概念，即在每个选择路径上只考虑当前节点及其子节点的情况，不受其他节点的影响。

回溯算法的基本思想是将问题的解空间抽象成一个树形结构，搜索过程就是在这个树上的深度优先遍历。每次递归调用都表示在问题的某一层面上的选择，当得到一个解或者无法继续前进时，返回上一层进行回溯，重新选择其他分支。因此，回溯算法可以看作是一种试错的思想。

回溯算法的原理可以总结为以下几点：

  1. 定义问题的解空间：将问题的解抽象为一个树形结构，树的节点表示问题的每个阶段的状态，路径表示选择的结果。
  2. 定义问题的约束条件：对于每个阶段的状态，定义合法的选择范围，即哪些分支可以选择。
  3. 定义问题的目标函数：确定何时得到一个解，即满足特定条件的路径。
  4. 利用深度优先搜索：从根节点开始，按照深度优先的顺序遍历解空间树，递归地在每个阶段做出选择。
  5. 判断是否需要回溯：当遇到无效的选择或者达到目标函数时，返回上一层进行回溯，重新选择其他分支。
  6. 得到所有解：持续搜索整个解空间，直到遍历完所有可能的选择，得到所有满足条件的解。

需要注意的是，回溯算法通常需要通过剪枝操作来减少不必要的搜索。剪枝操作可以根据具体问题的特性，在每个阶段的状态中提前排除一些明显不合法的选择，从而减少搜索的时间复杂度。

3.2 递归在回溯算法中的应用

回溯算法实际上是一种递归调用的方式，每次递归都会尝试一个选择，并进入下一层递归来处理更细分的问题。当满足某个终止条件时，递归会回溯到上一层，并尝试其他选择。

继续研究LeetCode77题，我们图示一下上面自己枚举所有答案的过程。

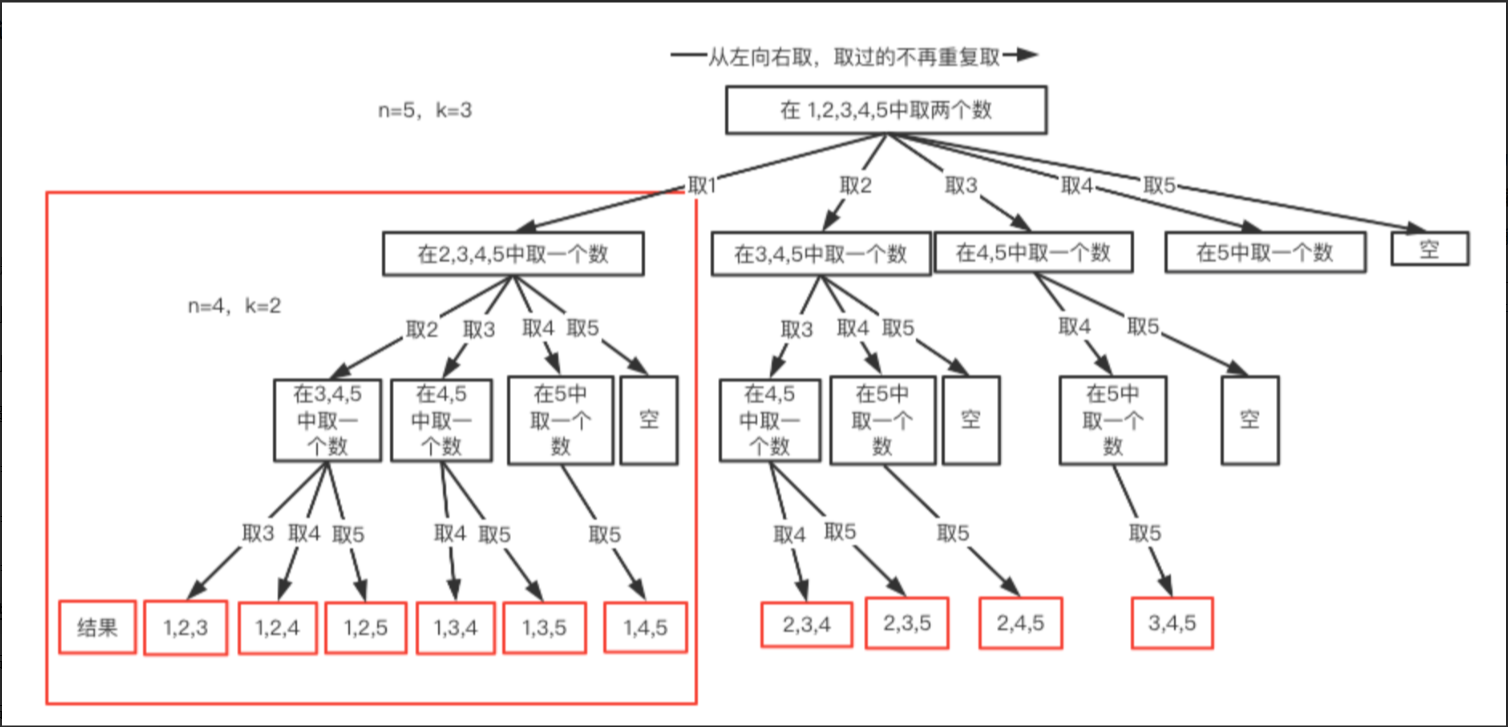
n=4时，我们可以选择的n有 {1,2,3,4}这四种情况，所以我们从第一层到第二层的分支有四个，分别表示可以取1，2，3，4。而且这里 从左向右取数，取过的数，不在重复取。 第一次取1，集合变为2，3，4 ，因为k为2，我们只需要再取一个数就可以了，分别取2，3，4，得到集合[1,2] [1,3] [1,4]，以此类推。

横向：

77.组合

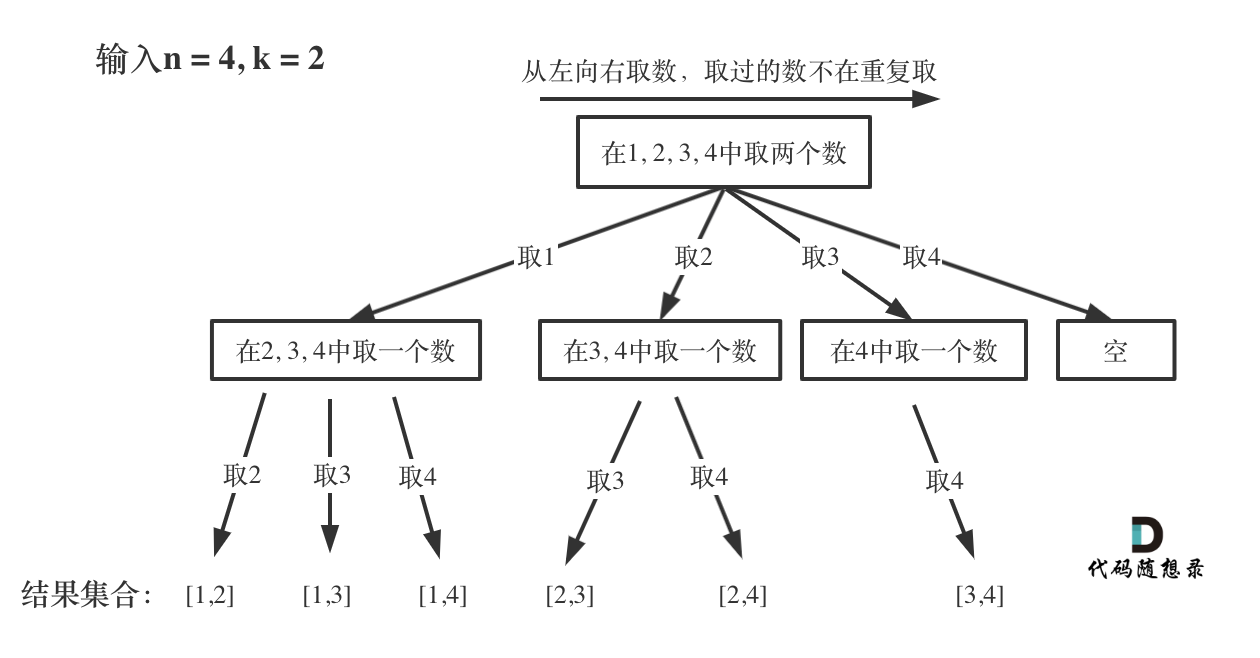
可以看出这棵树，一开始集合是 1，2，3，4， 从左向右取数，取过的数，不再重复取。

第一次取1，集合变为2，3，4 ，因为k为2，我们只需要再取一个数就可以了，分别取2，3，4，得到集合[1,2] [1,3] [1,4]，以此类推。

每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围。

图中可以发现n相当于树的宽度，k相当于树的深度。

那么如何在这个树上遍历，然后收集到我们要的结果集呢？

图中每次搜索到了叶子节点，我们就找到了一个结果。

相当于只需要把达到叶子节点的结果收集起来，就可以求得 n个数中k个数的组合集合。

在关于回溯算法，你该了解这些！中我们提到了回溯法三部曲，那么我们按照回溯法三部曲开始正式讲解代码了。

3.3 回溯法三部曲

3.3.1 递归函数的返回值以及参数

在这里要定义两个全局变量，一个用来存放符合条件单一结果，一个用来存放符合条件结果的集合。

代码如下：

public static List<List<Integer>> result = new ArrayList<>();  // 存放符合条件结果的集合
public static List<Integer> path = new ArrayList<>();  // 用来存放符合条件结果

其实不定义这两个全局变量也是可以的，把这两个变量放进递归函数的参数里，但函数里参数太多影响可读性，所以我定义全局变量了。

函数里一定有两个参数，既然是集合n里面取k个数，那么n和k是两个int型的参数。

然后还需要一个参数，为int型变量startIndex，这个参数用来记录本层递归的中，集合从哪里开始遍历（集合就是[1,…,n] ）。

为什么要有这个startIndex呢？

建议在77.组合视频讲解 (opens new window)中，07:36的时候开始听，startIndex 就是防止出现重复的组合。

从下图中红线部分可以看出，在集合[1,2,3,4]取1之后，下一层递归，就要在[2,3,4]中取数了，那么下一层递归如何知道从[2,3,4]中取数呢，靠的就是startIndex。

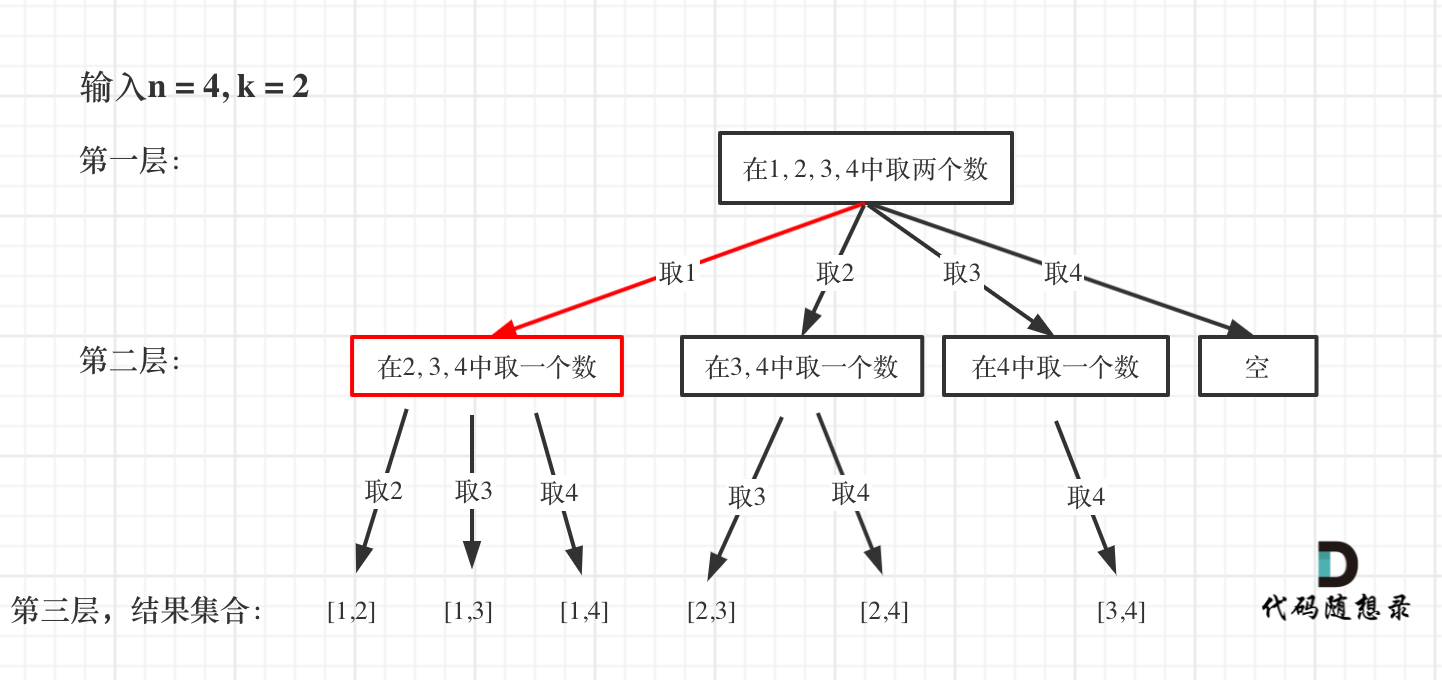
77.组合2

所以需要startIndex来记录下一层递归，搜索的起始位置。

那么整体代码如下：

public static List<List<Integer>> result = new ArrayList<>();  // 存放符合条件结果的集合
public static List<Integer> path = new ArrayList<>();  // 用来存放符合条件结果
void backtracking(int n, int k, int startIndex)
3.3.2 回溯函数终止条件

什么时候到达所谓的叶子节点了呢？

path这个数组的大小如果达到k，说明我们找到了一个子集大小为k的组合了，在图中path存的就是根节点到叶子节点的路径。

如图红色部分：

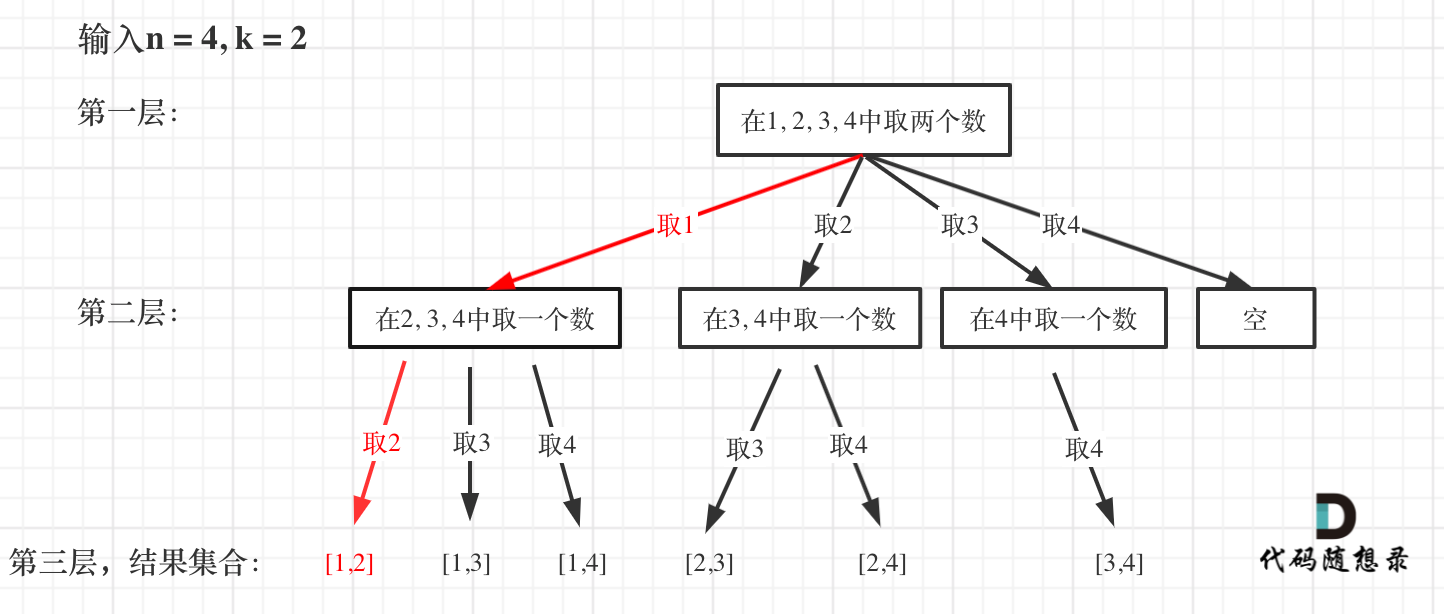
77.组合3

此时用result二维数组，把path保存起来，并终止本层递归。

所以终止条件代码如下：

if (path.size() == k) {
    result.add(new ArrayList<>(path));
    return;
}
3.3.3 单层搜索的过程

回溯法的搜索过程就是一个树型结构的遍历过程，在如下图中，可以看出for循环用来横向遍历，递归的过程是纵向遍历。

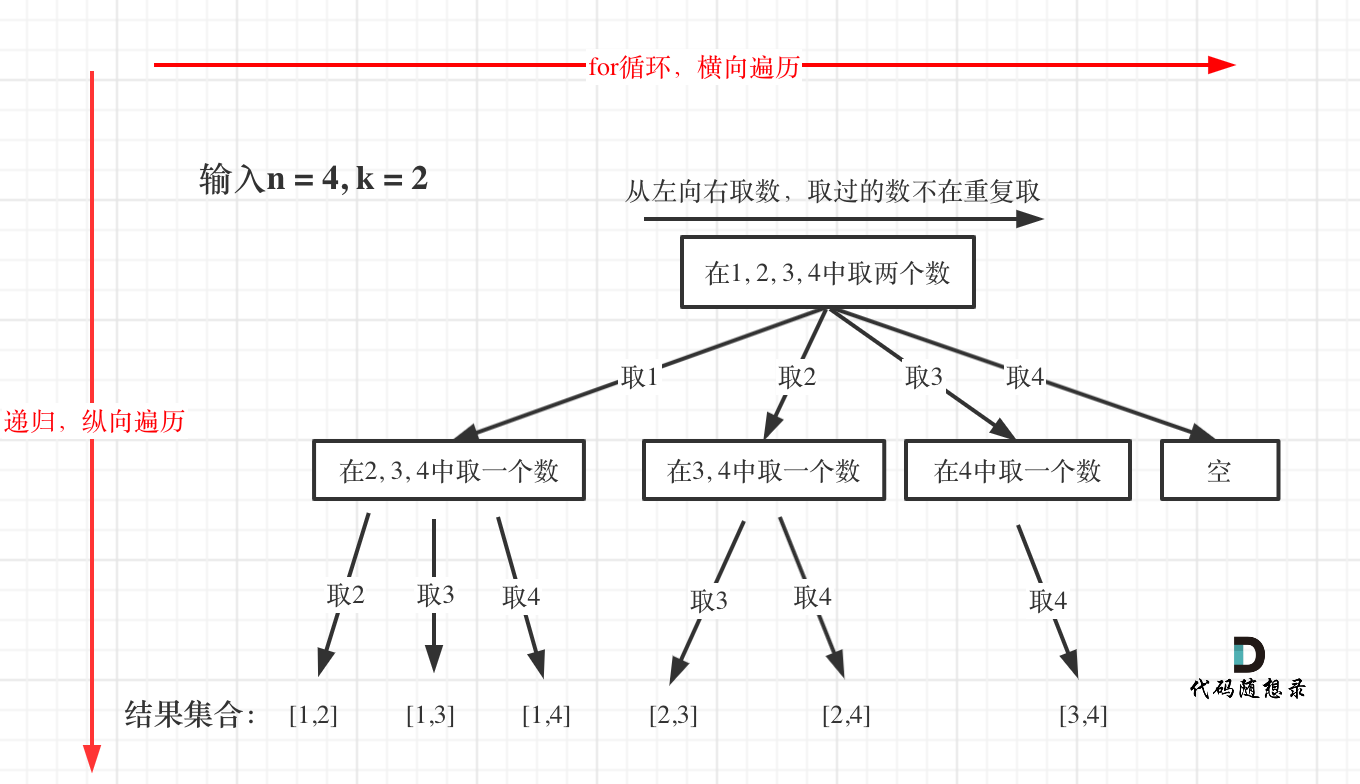
77.组合1

如此我们才遍历完图中的这棵树。

for循环每次从startIndex开始遍历，然后用path保存取到的节点i。

代码如下：

for (int i = startIndex; i <= n; i++) { // 控制树的横向遍历
    path.add(i);  // 处理节点
    backtracking(n, k, i + 1);  // // 递归：控制树的纵向遍历，注意下一层搜索要从i+1开始
    path.remove(path.size() - 1);  // 回溯，撤销处理的节点
}

可以看出backtracking（递归函数）通过不断调用自己一直往深处遍历，总会遇到叶子节点，遇到了叶子节点就要返回。

backtracking的下面部分就是回溯的操作了，撤销本次处理的结果。

关键地方都讲完了，组合问题java完整代码如下：

class Solution {
    private List<List<Integer>> result;  // 存放符合条件结果的集合
    private List<Integer> path;  // 用来存放符合条件结果

    private void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i <= n; i++) {
            path.add(i);  // 处理节点
            backtracking(n, k, i + 1);  // 递归
            path.remove(path.size() - 1);  // 回溯，撤销处理的节点
        }
    }

    public List<List<Integer>> combine(int n, int k) {
        result = new ArrayList<>();
        path = new ArrayList<>();
        backtracking(n, k, 1);
        return result;
    }
}
  • 时间复杂度: O(n * 2^n)
  • 空间复杂度: O(n)

还记得前面给出的回溯法模板么？

如下：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

对比一下本题的代码，是不是发现有点像！ 所以有了这个模板，就有解题的大体方向，不至于毫无头绪。

那假设，k等于3时，图应该是咋样？

image-20230904112327709

4. 图解为什么有个撤销的操作

4.1 回溯算法中的撤销操作的意义

撤销操作在回溯算法中非常重要，它能够帮助我们回到上一层递归，并尝试其他可能的选择。通过撤销操作，我们可以有效地减少搜索空间，节省时间和资源。

4.2 撤销操作的实现方法和技巧

撤销操作的实现方法通常是通过回溯函数的参数传递或全局变量来记录每次选择的状态，在回溯到上一层时进行恢复。此外，还可以使用标记数组等数据结构来辅助实现撤销操作。

4.3剪枝优化

我们说过，回溯法虽然是暴力搜索，但也有时候可以有点剪枝优化一下的。

在遍历的过程中有如下代码：

for (int i = startIndex; i <= n; i++) {
    path.add(i);  // 处理节点
    backtracking(n, k, i + 1);  // 递归
    path.remove(path.size() - 1);  // 回溯，撤销处理的节点
}

这个遍历的范围是可以剪枝优化的，怎么优化呢？

来举一个例子，n = 4，k = 4的话，那么第一层for循环的时候，从元素2开始的遍历都没有意义了。 在第二层for循环，从元素3开始的遍历都没有意义了。

这么说有点抽象，如图所示：

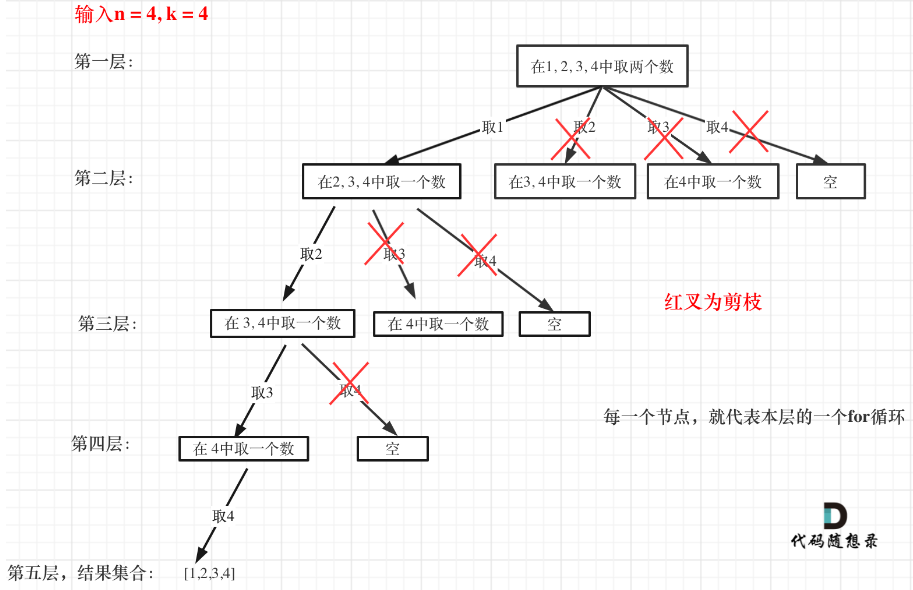
image-20230904113746196

图中每一个节点（图中为矩形），就代表本层的一个for循环，那么每一层的for循环从第二个数开始遍历的话，都没有意义，都是无效遍历。

所以，可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。

如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了。

注意代码中i，就是for循环里选择的起始位置。

for (int i = startIndex; i <= n; i++) {

接下来看一下优化过程如下：

  1. 已经选择的元素个数：path.size();
  2. 还需要的元素个数为: k - path.size();
  3. 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历

为什么有个+1呢，因为包括起始位置，我们要是一个左闭的集合。

举个例子，n = 4，k = 3， 目前已经选取的元素为0（path.size为0），n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。

从2开始搜索都是合理的，可以是组合[2, 3, 4]。

这里大家想不懂的话，建议也举一个例子，就知道是不是要+1了。

所以优化之后的for循环是：

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置

优化后整体代码如下：

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    
    public List<List<Integer>> combine(int n, int k) {
        backtracking(n, k, 1);
        return result;
    }

    /**
     * 每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围，就是要靠startIndex
     * @param startIndex 用来记录本层递归的中，集合从哪里开始遍历（集合就是[1,...,n] ）。
     */
    private void backtracking(int n, int k, int startIndex){
        //终止条件
        if (path.size() == k){
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i <= n - (k - path.size()) + 1; i++){
            path.add(i);
            backtracking(n, k, i + 1);
            path.removeLast();
        }
    }
}

5. 回溯热身一再论二叉树的路径问题

5.1 输出二叉树的所有路径

leetcode 257 二叉树的所有路径

根据上面提出的方式，回溯三部曲：

  1. 递归函数的返回值以及参数
private List<String> result = new ArrayList<>();

private void dfs(TreeNode root, StringBuilder sb) {
    
}
  1. 回溯函数终止条件
if (root == null) {
    return;
}

if (root.left == null && root.right == null) {
    result.add(sb.toString());
} else {
    dfs(root.left, sb);
    dfs(root.right, sb);
}
  1. 单层搜索的过程
private void dfs(TreeNode root, StringBuilder sb) {
        if (root == null) {
            return;
        }
        
        int len = sb.length();

        if (len > 0) {
            sb.append("->");
        }
        
        sb.append(root.val);
        
        if (root.left == null && root.right == null) {
            result.add(sb.toString());
        } else {
            dfs(root.left, sb);
            dfs(root.right, sb);
        }
        
        sb.setLength(len);
    }

最后的完整代码如下：

class Solution {
    private List<String> result = new ArrayList<>();
    
    public List<String> binaryTreePaths(TreeNode root) {
        dfs(root, new StringBuilder());
        return result;
    }

    private void dfs(TreeNode root, StringBuilder sb) {
        if (root == null) {
            return;
        }
        
        int len = sb.length();

        if (len > 0) {
            sb.append("->");
        }
        
        sb.append(root.val);
        
        if (root.left == null && root.right == null) {
            result.add(sb.toString());
        } else {
            dfs(root.left, sb);
            dfs(root.right, sb);
        }
        
        sb.setLength(len);
    }
}

5.2 路径总和问题

leetcode 113. 路径总和 II

这题类似上一题，写的方式是一样的，只需要改单层搜索的过程，这里

注意：路径结束会有个撤销的动作，这个特别重要

class Solution {
    private List<List<Integer>> result = new ArrayList<>();
    private List<Integer> path = new ArrayList<>();

    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        computePathSum(root, targetSum, 0);
        return result;
    }

    private void computePathSum(TreeNode root, int targetSum, int pathLen){
        if(root == null){
            return;
        }

        pathLen += root.val;
        path.add(root.val);

        if(root.left == null && root.right == null){
            if(pathLen == targetSum){
                result.add(new ArrayList<>(path));
            }
        }

        computePathSum(root.left, targetSum, pathLen);
        computePathSum(root.right, targetSum, pathLen);

        path.remove(path.size() - 1);
    }
}

over，入门结束~~

XiaoZhi-paperfly
关注
  • 0
    点赞
  • 踩
  • 0
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
算法通关村第一关-链表青铜挑战笔记
10-28
源代码
算法通关村第十八关——回溯青铜挑战笔记
m0_46098809的博客
09-08 124
"放下前任"：path数组维护了当前所走的路径，因此在枚举当前元素后，以递归的形式返回前，应先将当前枚举的元素移除path数组（就好比开始新化学实验之前，需要清理仪器设备，不能让前面的实验杂质干扰影响正在进行的实验）。第二，局部枚举：维护一个path数组，先将当前枚举的节点加入path数组，然后再枚举左右孩子节点，若当钱枚举的节点如果是叶子结点，将path数组加入ans数组中；此外，回溯模版所能解决的问题也是十分明确的，例如：组合、分割、子集、排列、棋盘等，但是具体问题具体分析，回溯模版也会有灵活的调整。
算法通关村第十八关——回溯热门问题（白银）
Hai_Helloyou的博客
09-05 140
对于英文字母，它们的 ASCII 码中的第 6 位表示大小写信息，其中大写字母的第 6 位为 0，小写字母的第 6 位为 1。同时，由于异或运算是可逆的，所以在递归回溯时，再次对同一个字符进行异或操作，可以恢复原来的大小写形式。我们发现大写字符与其对应的小写字符的 ASCII 的差为 32，32 这个值如果敏感的话，它是 2^5，在编程语言中，可以表示为 1 << 5。则，可以使用boolean[]可以记录，用数组的方式，记录true，false（说实话，我也是第一次用。异或运算（^）是一种位运算符。
算法通关村第十八关青铜挑战——透析回溯的模板
m0_74469506的博客
11-30 239
详细讲解什么是回溯？回溯的模板是什么？详细讲解两道入门小题帮你理解回溯
算法通关村第十八关：青铜挑战-回溯是怎么回事
qq_41662142的博客
09-08 452
深度优先搜索就是从根节点开始一直找到叶子结点，这里可以先判断当前节点是不是叶子结点，再决定是不是向下走，如果是叶子结点，我们就增加一条路径。从回溯的角度分析，得到第一条路径ABD之后怎么找到第二条路径ABE，这里就是先将D撤销，然后再继续递归就可以了。这就是组合类型问题，除此之外，子集、排列、切割、棋盘等方面都有类似的问题，我们需要找到更好的方式。回溯不是万能的，解决的问题也是非常明确的，例如组合、分割、子集、排列、棋盘等。所有的回溯都是一个大框架，因此透彻理解回溯的框架是解决一切回溯问题的基础。
算法通关村第十八关-青铜挑战回溯是怎么回事
sytdsqzr的博客
12-08 1295
大家好我是苏麟 , 今天聊聊回溯是怎么个事 .回溯是最重要的算法思想之一，主要解决一些暴力枚举也搞不定的问题，例如组合、分割、子集、排列，棋盘等。从性能角度来看回溯算法的效率并不高，但对于这些暴力都搞不定的算法能出结果就很好了，效率低点没关系我们利用LeetCode 77 组合题来了解回溯 .
算法通关村第十五关——超大规模数据场景青铜挑战笔记
m0_46098809的博客
08-31 117
例如：给定一个数组，其数据范围在1-32000，数据流远远不断到来，使用int类型的数组标记这些元素，需要32000个int块，所占用的内存大小就是128KB，但是如果使用最小单位Bit来标记这些元素，仅仅需要32000个Bit，所占用的内存大小就是4000B，也就是1000个int块。当元素确定存放位置后，该位置的比特为0，则可以存放，每次存放应使用“或”运算，不能修改其他已经存放元素的位置。，如果文件太大，无法在内存中放下，需要考虑将大文件分成若干小块，先处理每个块，然后再逐步得想要的结果。
[Go版]算法通关村第十八关青铜——透析回溯的模版
trinityleo5的博客
10-25 532
[Go版]算法通关村第十八关青铜——透析回溯的模版
算法通关村第十九关——动态规划是怎么回事（青铜）
Hai_Helloyou的博客
09-07 530
动态规划是一种解决复杂问题的算法思想，它将一个大问题分解为多个相互关联的子问题，并通过递推关系将子问题的解整合起来，最终得到原问题的解。动态规划的核心思想是将问题划分为重叠子问题，并存储子问题的解，避免重复计算。动态规划通常用于求解最优化问题，如求解最长公共子序列、最短路径、背包问题等。它的基本步骤包括定义状态、设置初始状态、确定状态转移方程和计算最优解。动态规划的优点是减少了重复计算，提高了算法效率，但它也需要额外的空间来存储子问题的解，因此在使用动态规划时需要权衡时间和空间的开销。
算法通关村第十八关 | 青铜 | 回溯
星不易的博客
12-11 208
回溯可以视为递归的拓展，有着明确的解题模板。很大的不同之处是有一个撤销处理结果的操作，但是大框架就是遍历 N 叉树。回溯主要解决暴力枚举都解决不了的问题。回溯完整代码示例：返回 1 到 n 中所有可能的 k 个数的组合。
算法分析论文——回溯算法的应用.zip
10-19
算法分析论文——回溯算法的应用 包括算法的即便额概念，思想，回溯法应用及其在某些方面的改进
五大常见算法策略之——回溯策略，算法数据结构
04-07
五大常见算法策略之——回溯策略，算法数据结构 五大常用算法
五大常用算法——回溯算法详解及经典例题，算法数据结构 五大常用算法
04-07
五大常用算法——回溯算法详解及经典例题，算法数据结构 五大常用算法
算法训练Day26 | 332.重新安排行程 ● 51. N皇后 ● 37. 解数独
WIIIter的博客
05-08 248
【代码】算法训练Day26 | 332.重新安排行程 ● 51. N皇后 ● 37. 解数独。
1080：余数相同问题
如果没有特别说明，c++都是基于GCC-4.9.2运行的
05-11 366
【代码】：1080：余数相同问题
找第二大的数（分治法）
最新发布
2201_75525567的博客
05-11 296
这段代码通过递归的方式，将数组分为两半，并分别找出左半部分和右半部分的两个最大数，然后比较这四个数的大小，得到第二大的数。这段代码是用来找出数组中第二大的数的。
从零学算法6
m0_53256503的博客
05-11 971
之后，你的输出需要从左往右逐行读取，产生出一个新的字符串，比如：“PAHNAPLSIIGYIR”。将一个给定字符串 s 根据给定的行数 numRows ，以从上往下、从左到右进行 Z 字形排列。输入：s = “PAYPALISHIRING”, numRows = 3。输入：s = “PAYPALISHIRING”, numRows = 4。输入：s = “A”, numRows = 1。输出：“PAHNAPLSIIGYIR”输出：“PINALSIGYAHRPI”
【算法】逃离大迷宫
m0_73209194的博客
05-08 295
leetcode 1036 逃离大迷宫
java子集和数问题回溯法算法_子集和数问题——回溯法
06-10
回溯法是一种解决这个问题的常见算法。 具体的解决方法是：首先定义一个数组来存储选择的结果，假设这个数组叫做solution。然后从集合的第一个元素开始，尝试将它加入solution中，如果加入后solution中的元素和仍然...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值