分形树详细教程

最新推荐文章于 2022-05-22 01:50:22 发布
最新推荐文章于 2022-05-22 01:50:22 发布
阅读量5.9k 收藏 40
点赞数 10
文章标签： c#
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/hanhandeguajian/article/details/119786176
版权
本文介绍了如何利用分形理论创建美丽的分形树，通过递归算法模拟自然界树木的生长结构。作者展示了从简单图形到复杂形态的过程，并实现了文件保存与打开功能。此外，还探讨了如何通过随机变量生成多样化的树形，以及添加落花效果，创造出樱花树的视觉效果。实验结果表明，分形在艺术创作中的潜力无穷。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

分形树详细教程

一、引言

分形是自然界的几何学。----
-曼德勃罗（分形理论创始人）

通过本次学习,学到了如何制作分形树 并且被他深深吸引,最终,也能做出一些如下:

落花的凤凰树,落花的紫荆花树,樱花花瓣飘落的树与落花的蓝花楹树
在这里插入图片描述

任务

2.2 参考分形的概念，绘制分形树或者其他分形图形。要求可以对图形进行保存和打开等操作。

http://www.matrix67.com/blog/archives/6231

https://www.zhihu.com/question/271643290/answer/525019532

二、实验环境

Visual stdio 2017
Windows窗体应用

三、实验过程

思路

1.分形概念的提出与分形理论的建立

2.创建窗体

3.生成分形树

4.实现文件保存与打开 及Bitmap 类

5.分形树与其衍生出的其他分形图形 效果展示

1.分形概念的提出与分形理论的建立

分形的英文为 fractal，是由美籍法国数学家曼德勃罗（Benoit Mandelbrot）创造出来的，此词源于拉丁文形容词 fractus，对应的拉丁文动词是 frangere（破碎、产生无规则碎片），此外，此词与英文的 fraction（碎片、分数）及 fragment（碎片）具有相同的词根。在20世纪70年代中期以前，曼德勃罗一直使用英文 fractional一词来表示他的分形思想。因此，取拉丁词之头，撷英文之尾所合成的 fractal，本意是不规则的、破碎的、分数的。曼德勃罗是想用此词来描述自然界中传统欧氏几何学所不能描述的一大类复杂无规则的几何对象。例如，蜿蜒曲折的海岸线、起伏不定的山脉、粗糙不堪的断面、变幻无常的浮云、九曲回肠的河流、纵横交错的血脉、令人眼花缭乱的满天繁星等。它们的共同特点是极不规则或极不光滑。直观而粗略地说，这些对象都是分形。

1975年，曼德勃罗出版了他的法文专著《分形对象∶形、机遇与维数》（Les objects fractals∶ forme，hasardetdimension），标志着分形理论的正式诞生，1977年他出版了该书的英译本。1982年曼德勃罗的另一部历史性著作《大自然的分形几何学》与读者见面。该书虽然是前书的增补本，但在曼德勃罗看来却是分形理论的"宣言书"，而在分形迷的眼中，它无疑是一部"圣经"。该书旁征博引、图文并茂，从分形的角度考察了自然界中的诸多现象，引起了学术界的广泛注意，曼德勃罗因此一举成名。
此后，一直持续的分形热引起了全世界众多科学家和学者的注意，他们在各自领域中的研究工作，使分形理论遍地开花。

2.创建窗体

创建一个画布,一些控件与按钮,下拉菜单,滚动条等等

最终结果结果如图所示:
在这里插入图片描述

为了让界面更加好看, 我采用一张色卡,用PS取色, 提取其中的墨绿色作为背景, 浅橙色作为树干

墨绿色作为背景

this.picBoxCanvas.BackColor = Color.FromArgb(64, 83, 81);//墨绿色背景色

浅橙色作为树干

treeTrunkPen = new Pen(Color.FromArgb(181, 143, 107));//新建树干画笔

3.生成分形树

画出画面DrawScene()函数:

由于画线函数graphics.DrawLine()只能接受float类型
所以 y0 ,height, width ,xloc0 等变量皆用float类型

初始化树 使得刚生成的树位于画面最中央

float xloc0 = width / 2.0f;
float yloc0 = (y0 + height) - YOffset;

初始化树位置展示:
画出画面完整代码:

private void DrawScene()
	{
		float y0 = 0.0f;
		float height = this.picBoxCanvas.Height;//是画布的高
		float width = this.picBoxCanvas.Width;是画布的宽
        //使得初始化的树处于最中间
        float xloc0 = width / 2.0f;
		float yloc0 = (y0 + height) - YOffset;

		float xloc1 = xloc0;
		float yloc1 = yloc0 - Length;
		//画树枝
		DrawBranch(settings.Depth, xloc0, yloc0, settings.Length, initBranchAngle, scaledLength, settings.Angle);
	}
画树枝

接下来 就要实现画树枝功能:

各个变量定义:

/// <summary>
/// 画树枝
/// </summary>
/// <param name="depth">递归深度</param>
/// <param name="X">X 表示树枝的起点</param>
/// <param name="Y">Y 表示树枝的起点</param>
/// <param name="length">表示树枝的长度</param>
/// <param name="theta">表示树枝的角度</param>
/// <param name="scaledLength">按比例计算连续分支的数量</param>
/// <param name="deltaTheta">连续分支的角度变化</param>
树枝的顶点

因此变幻时

 // x1, y1 计算分支接结尾
    // sin等于对边比斜边，cos等于邻边比斜边(长度等于斜边)
    x1 = X + length * (float)Math.Cos(theta * RadiansPerDegree); // 增加x(让它从左到右变幻)
    y1 = Y - length * (float)Math.Sin(theta * RadiansPerDegree); // 减少y(让它从下到上变幻) 
                                                                 //比如y的-减变成+ 弄反了就会倒着长
树干的宽度/粗细

定义树干的宽度

 treeTrunkPen.Width = treeTrunkWidths[depth];

此处的数组用到了上面自定义的

递增的数量使得最终的树干会有不同粗细 更好地模拟树的生长

 //树干粗
private int[] treeTrunkWidths = { 0, 1, 2, 3, 4, 6, 9, 11, 14, 17 };

由于三叉树时会非常庞大杂乱 因此没有设置很长数组的树宽

画出一条线:在X, Y, x1, y1 间画一条线 这个函数只能接受float类型

graphics.DrawLine(treeTrunkPen, X, Y, x1, y1);//在X, Y, x1, y1 间画一条线
递归实现树的生长

自然界中的树也具有分形结构。一根主干生长出两个侧干，每个侧干又生长出两个侧干，以此类推，便生长出疏密有致的结构。这样的生长结构，用分形的递归算法也能模拟出来，但不会像自然界中的树那么自然。
(因此在本次实验中,我尝试加入随机值 使得树更加自然生态)

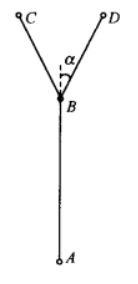
在这里插入图片描述

  1. 递归分形树一（1）如上图所示是分叉树的生成元，利用递归算法生成分叉树的过程，实际上就是将这个生成元在每一个层次上不断重画的过程，具体步骤如下∶
① 设A点坐标为（x，y），B点坐标为（xo，y0），C点坐标为（x1,y1），D点坐标为（x2，y2），L为树干的长度，α为枝干与主干的夹角。
② 绘制主干 AB，即（x，y）-（xo，yo）直线。
③ 计算C点坐标，L=scaledLength×L，x=x+L×cosα，y=y0-L×sina。
④ 计算D点坐标，L=scaledLength×L，x1=xo+L×cos（-α），y1=y0-L×sin（-α）。
⑤ 将步骤②中x→x，y0→y，x1→x0，y1→y0，再绘制（x，y）-（x0，y0）直线，即画分枝BC。
⑥ 将步骤②中x→x，y0→y，x2→x0，y2→y0，再绘制（x，y）-（xo，y0）直线，即画分枝BD。
⑦重复执行步骤③～步骤⑥，直至完成递归次数。

注: 初始化时,我将scaledLength调整为四分之三

private const float scaledLength = 0.75f;

再者,在这个实例里 通过让depth–从而在画分形树的过程中也不断使树干变细,形成树的效果

同时,也实现了三叉树的生成,以下是二者的对比:

1.生成二叉树过程:

递归调用----->绘制右边 +连续分支的角度变化

递归调用----->绘制左边 +连续分支的角度变化

2.生成三叉树过程:

递归调用----->绘制右边 +连续分支的角度变化

递归调用----->绘制中边 (不用变幻角度)

递归调用----->绘制左边 +连续分支的角度变化

   // 如果不是顶部的分支，画出连接的分支
    if (depth > 1)
    {
        //三叉树只是比二叉树多了一个中间的分支
        // 递归调用-绘制右边 +deltaTheta  (二叉+三叉)
        DrawBranch(depth - 1, x1, y1, (length * scaledLength) + randomnessRightHandSide, (theta + deltaTheta) + randomnessRightHandSide, scaledLength, deltaTheta);

        if (settings.RandomThirdBranch)//随机三叉树
        {
            int drawMiddleBranch = randomMiddleBranch.Next(0, 2);
            if (drawMiddleBranch == 0)
            {
                // 绘制中间
                DrawBranch(depth - 1, x1, y1, (length * scaledLength) + randomnessLeftHandSide, theta + randomnessLeftHandSide, scaledLength, deltaTheta);// randomnessRightHandSide随机值
            }
        }
        else if (settings.ThreeBranches)//三叉树
        {
            // 绘制中间
            DrawBranch(depth - 1, x1, y1, (length * scaledLength) + randomnessLeftHandSide, theta + randomnessLeftHandSide, scaledLength, deltaTheta);
        }

        // 递归调用-绘制左边 -deltaTheta  (二叉+三叉)
        DrawBranch(depth - 1, x1, y1, (length * scaledLength) + randomnessLeftHandSide, (theta - deltaTheta) + randomnessLeftHandSide, scaledLength, deltaTheta);
    }
    // 如果是顶点叶子
    else if (depth == 1)
    {
        if (settings.EndLeaves)//可以画叶子或者画
        {
            // 到目前为止，结束叶子只是一个圆(bitmap也可)
            graphics.DrawArc(endLeavesPen, x1 - 2, y1 - 2, 6, 6, 0, 360);
            graphics.DrawArc(endLeavesPen, x1 - 2, y1 - 2, 4, 4, 0, 360);
        }
    }
}
画叶子或者花

点击以下窗体应用的面板
在这里插入图片描述

 else if (depth == 1)//如果到了叶子
    {
        if (settings.EndLeaves)//可以画叶子或者画
        {
            // 到目前为止，结束叶子只是一个圆(bitmap也可)
            graphics.DrawArc(endLeavesPen, x1 - 2, y1 - 2, 6, 6, 0, 360);//圈
            graphics.DrawArc(endLeavesPen, x1 - 2, y1 - 2, 4, 4, 0, 360);
        }
    }

展示:
在这里插入图片描述
我们自然会想到,怎样增加更多树叶或花瓣(甚至是树上的积雪呢)

所以可以对这个代码进行改进

graphics.DrawArc(endLeavesPen, x1 - 2, y1 - 2, 6, 10, 0, 180);
graphics.DrawArc(endLeavesPen, x1 - 4, y1 - 4, 3, 4, 0, 180);
graphics.DrawArc(endLeavesPen, x1 - 3, y1 - 3, 6, 10, 0, 180);
graphics.DrawArc(endLeavesPen, x1 - 2, y1 - 2, 3, 4, 0, 180);
graphics.DrawArc(endLeavesPen, x1 - 6, y1 - 7, 6, 10, 0, 180);
graphics.DrawArc(endLeavesPen, x1 - 2, y1 - 3, 3, 4, 0, 180);

在这里插入图片描述

实现随机
 if (settings.RandomThirdBranch)//随机三叉树
        {
            int drawMiddleBranch = randomMiddleBranch.Next(0, 2);//这里完成随机分枝数
            if (drawMiddleBranch == 0)
            {
                // 绘制中间
                DrawBranch(depth - 1, x1, y1, (length * scaledLength) + randomnessLeftHandSide, theta + randomnessLeftHandSide, scaledLength, deltaTheta);// randomnessRightHandSide 实现随机值
            }
        }

在这里插入图片描述
函数代码:

private void DrawBranch(int depth, float X, float Y, float length, float theta, float scaledLength, float deltaTheta)
{
    float x1;
    float y1;

    // x1, y1 计算分支接结尾
    // sin等于对边比斜边，cos等于邻边比斜边(长度等于斜边)
    x1 = X + length * (float)Math.Cos(theta * RadiansPerDegree); // 增加x(让它从左到右变幻)
    y1 = Y - length * (float)Math.Sin(theta * RadiansPerDegree); // 减少y(让它从下到上变幻) 
                                                                 //比如y的-减变成+ 弄反了就会倒着长

    treeTrunkPen.Width = treeTrunkWidths[depth];
    graphics.DrawLine(treeTrunkPen, X, Y, x1, y1);//在X, Y, x1, y1 间画一条线

    // 如果不是顶部的分支，画出连接的分支
    if (depth > 1)
    {
        //三叉树只是比二叉树多了一个中间的分支
        // 递归调用-绘制右边 +deltaTheta  (二叉+三叉)
        DrawBranch(depth - 1, x1, y1, (length * scaledLength) + randomnessRightHandSide, (theta + deltaTheta) + randomnessRightHandSide, scaledLength, deltaTheta);// randomnessRightHandSide随机值

        if (settings.RandomThirdBranch)//随机三叉树
        {
            int drawMiddleBranch = randomMiddleBranch.Next(0, 2);
            if (drawMiddleBranch == 0)
            {
                // 绘制中间
                DrawBranch(depth - 1, x1, y1, (length * scaledLength) + randomnessLeftHandSide, theta + randomnessLeftHandSide, scaledLength, deltaTheta);
            }
        }
        else if (settings.ThreeBranches)//三叉树
        {
            // 绘制中间
            DrawBranch(depth - 1, x1, y1, (length * scaledLength) + randomnessLeftHandSide, theta + randomnessLeftHandSide, scaledLength, deltaTheta);
        }

        // 递归调用-绘制左边 -deltaTheta  (二叉+三叉)
        DrawBranch(depth - 1, x1, y1, (length * scaledLength) + randomnessLeftHandSide, (theta - deltaTheta) + randomnessLeftHandSide, scaledLength, deltaTheta);
    }
    // 如果是顶点叶子
    else if (depth == 1)
    {
        if (settings.EndLeaves)//可以画叶子或者画
        {
            // 到目前为止，结束叶子只是一个圆(bitmap也可)
            graphics.DrawArc(endLeavesPen, x1 - 2, y1 - 2, 6, 6, 0, 360);
            graphics.DrawArc(endLeavesPen, x1 - 2, y1 - 2, 4, 4, 0, 360);
        }
    }
}

4.实现文件保存与打开 及Bitmap 类

Bitmap 类

Bitmap 类是 Image 类的派生类，通过它可以载入并显示各种位图图像。图像由一系列

的像素构成，知道每个像素的信息，就知道了整个图像。位图图像就通过存储所有像素的

信息来描述图像的。GDI+支持多种图像文件格式，包括 BMP、GIF、JPEG、PNG、TIFF、

EXIF 等。

bitmap里面要有图片

bitmap = new Bitmap(picBoxCanvas.Width, picBoxCanvas.Height)

Path.GetExtension返回指定路径中的扩展名

如果后缀名是.bmp .png .jpeg .jpg .gif 都可以保存

文件保存与打开:

namespace Fractal
{
	class FileManager
	{
		public void SaveFileAsBitmap(System.Windows.Forms.PictureBox picBoxCanvas, String filename)
		{
			using (var bitmap = new Bitmap(picBoxCanvas.Width, picBoxCanvas.Height))
			{
				picBoxCanvas.DrawToBitmap(bitmap, picBoxCanvas.ClientRectangle);
				ImageFormat imageFormat = null;

				var extension = Path.GetExtension(filename);
				switch (extension)
				{
					case ".bmp":
						imageFormat = ImageFormat.Bmp;
						break;
					case ".png":
						imageFormat = ImageFormat.Png;
						break;
					case ".jpeg":
					case ".jpg":
						imageFormat = ImageFormat.Jpeg;
						break;
					case ".gif":
						imageFormat = ImageFormat.Gif;
						break;
					default:
						throw new NotSupportedException(String.Format("File extension {0} is not supported", extension));
				}

				bitmap.Save(filename, imageFormat);
			}
		}
	}
}

保存后:
在这里插入图片描述
5分形树与其衍生出的其他分形图形 效果展示

利用随机变量 可以生成一些神奇又优美的树

奇怪的树
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
加入落花效果的樱花树:

 //以下是落花效果
                    //graphics.DrawArc(endLeavesPen, x1 + 20, y1 + 21, 6, 10, 0, 180);
                    //graphics.DrawArc(endLeavesPen, x1 + 24, y1 + 23, 6, 10, 0, 180);
                    //graphics.DrawArc(endLeavesPen, x1 - 27, y1 + 25, 6, 10, 0, 180);
                    //graphics.DrawArc(endLeavesPen, x1 - 15, y1 - 16, 6, 10, 0, 180);
                    //graphics.DrawArc(endLeavesPen, x1 + 20, y1 + 21, 6, 10, 0, 180);
                    //graphics.DrawArc(endLeavesPen, x1 - 37, y1 + 35, 6, 10, 0, 180);

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

四、总结

分形树采用递归的方法 从简单的重复迈向复杂 而用随机树创建出来的树和自然界中的树如此相似 让人不禁设想,是不是上帝用了分形算法创造出这些树和世间很多东西呢

总之, 分形真的很让人着迷!!!
影子__
关注
Python分形树（完整代码）
Python、C++、HTML、Java
12-15 5317
Python绘制一棵分形树的完整代码。和main。其中，函数是一个递归函数，用于绘制分支的每一部分，而main函数则是程序的入口，负责设置绘图环境、初始化画笔状态、调用绘制函数等。我们将逐一分析这两个函数的作用及实现细节。通过这段代码，我们不仅能够理解如何利用递归绘制分形树，还能够深入学习如何使用Turtle库进行绘图。分形树的绘制展示了递归思想在图形绘制中的应用，同时也为我们提供了一个简洁而美观的图形展示方法。
分形树最简单单的画法
11-08
分形几何学的基本思想：客观事物具有自相似性的层次结构，局部和整体在形态，功能，信息，时间，空间等方面具有统计意义上的相似性，称为自相似性，自相似性是指局部是整体成比例缩小的性质。
分形算法 分形树 很炫的
03-21
用VC实现的树的分形算法，从树开始生长到落叶
分形之树（Tree）
weixin_34123613的博客
10-14 268
      似乎每一个有关分形的教程都要讲到分形树，大概是因为树是生活中最常见的分形实物吧。这一节将展示下如何一步一步地生长出一棵树来。其实现算法不难，就是在每一次生长迭代中，使线段生长出几条新的线段来。 核心代码: static void FractalTree(const Vector3&amp; vStart, const Vector3&amp; vEnd, ...
分形树
qq_31724343的博客
03-21 1479
要画一颗分形树，使用turtle 分形图形的特征：子图与自身相似，很容易想到递归。 要点在于定义初末状态。调用结束时，让turtle回到开始调用时的位置，并且方向与来时方向一致。 public static void drawMyhelper(Turtle tur,int lenth,double angle) { if(lenth<=4) { return ; ...
分形树算法之一
java开发指南博客 【转载】
08-14 504
drawLeaf(CClientDC dc, int x, int y, int L, double A) { CPen NewPen(PS_SOLID,1,RGB(0,0,0));// CPen OldPen(PS_SOLID,1,RGB(255,255,255)); if(isD)dc.SelectObject(NewPen); else dc.SelectOb...
递归与Python Turtle分形树绘制详解（包含详细的完整的程序和数据）
最新发布
10-10
本文详细阐述了如何使用Python的turtle库进行递归函数的设计，并具体演示了一个绘制分形树的例子。主要内容涵盖递归的基础概念，turtle的基本操作以及如何用它们组合在一起创建一个动态可视化的递归模型。通过实际...
fenxingGUI.rar_GUI 图像处理_matlab分形树_分形树 matlab
07-14
通常，这样的文本文件会包含作者的联系方式、项目的详细说明或者使用教程。 总的来说，这个资源为图像处理专业人士提供了一个用MATLAB实现的分形树GUI工具，通过交互式的界面，用户可以探索和理解分形树的特性，...
使用Metapost绘制Markov链与分形树的图像教程
该标题指向的文档展示了使用metapost绘制“Markov链”和“分形树”。 1. **Markov链（马尔可夫链）**：是一种随机过程，其中下一个状态的转移概率仅依赖于当前状态，与之前的状态历史无关，这种性质称为无记忆性。...
Javascript实现简单的分形树
05-07
先垂直绘制一根线段，然后在线段长度的三分之一处和三分之二处分别以 固定夹角绘制另外两根线段，长度分别 为原线段的2/3和1/3. 如此反复，直至线段长度小于某个较小的值。
OpenGL实现分形树设计与绘制教程（附源码与报告）
本知识点围绕“计算机图形学—OpenGL（C++）分形树的设计”这一主题展开。该主题涵盖了分形树的计算机图形学生成、OpenGL的图形渲染技术、以及C++编程语言在图形学中的应用。以下详细说明各知识点： ### 分形树的...
VS2008环境下OpenGL实现的分形树教程
在信息技术领域，分形树是一个常见的图形生成示例，而使用Visual Studio 2008结合OpenGL技术开发此类项目，能够让开发者深入理解图形编程以及OpenGL的应用。以下将详细讲解该知识点。 首先，Visual Studio 2008是一...
数据结构20：递归可视化（分形树）
xddwz的博客
09-09 2526
一、图示 前面的递归算法展现了其简单而强大的一面，但还是难有个直观的概念，下面通过递归作图来展现递归调用的视觉影响力。 1、python的海龟作图系统turtle module python内置，随时可用，以LOGO语言的创意为基础 其意象是模拟海龟在沙滩上爬行而留下的足迹 操作： 爬行：forward(n), backward(n) 转向：left(a), right(a) 抬笔放笔：penup(a), pendown() 笔属性：pensize(n), pencolor(c).
Algorithm之绘制分形树
daisyr07
04-29 1219
绘制分形树 1.1题目描述 如下图所示，先垂直绘制一根线段，然后在线段长度的三分之一处和三分之二处分别以固定夹角绘制另外两根线段，长度分别为原线段的2/3和1/3. 如此反复，直至线段长度小于某个较小的值。其中，线条颜色以及长度，夹角都可以自行进行微调。 1.2 问题分析与解决思路 1.2.1 问题分析 问题需要解决如何绘制分形树？可以将绘制过程分解一下，然后去分析。 这是绘制的第一步： 可...
分形（二）——分形树
改变世界的力量
07-14 2629
分形（二）——分形树 上次我们画出了谢尔宾斯基三角形，这次我们所画分形图形同样也是比较简单的——分形树，记得在上次的递归里~我们传入的参数是所绘的点的坐标，但这种方法并不一定的最好的，在绘制分形图案的时候，使用递归，所传参数应根据实际情况来定：（可以是角度，变长等） 同学们可以自己也试着画一下分形：这是今天的题目： 分形树一次递归调用：   分形树两次递归调用：     分形树...
分形树——python递归
weixin_66030644的博客
05-22 3345
分形通常被定义为“一个粗糙或零碎的几何形状，可以分成数个部分，且每一部分都（至少近似地）是整体缩小后的形状”。分形树则顾名思义——亦即理论上无论放大多少倍，都具有相同形状。从单个树枝开始推广到整个分形树。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值