(1)short
C语言中,short是定义一种整型变量家族的一种
长度:
依据程序编译器的不同short定义的字节数不同。
标准定义short短整型变量不得低于16位,即两个字节。编译器头文件夹里面的limits.h定义了short能表示的大小:SHRT_MIN~SHRT_MAX。在32位平台下如windows(32位)中short一般为16位。
若规定编译器规定short为2字节,则:
unsigned short i; i可以表示0~65535(0~2^16-1)
signed(默认)short i; i可以表示-32768~+32767(-2^(16-1)~2^(16-1)-1)
(2)int
C语言中,int是定义一种整型变量家族的一种。
长度:
目前在一般的电脑中,int占用4字节,32比特,数据范围为-2147483648~2147483647[-2^31~2^31-1]
在之前的微型机中,int占用2字节,16比特,数据范围为-32768~32767[-2^15~2^15-1]
unsigned int 表示无符号整数,数据范围为[0~2^32-1]
除了short、int类型之外,还有long、long long类型可以表示整数。
以下对范围求取进行说明。
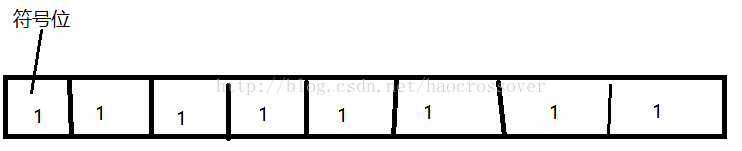
图1
以8位进行说明,16位,32位,64位类似。
第一位为符号位,0正,1负。假定数据类型的长度为一个字节8位。对有符号整型进行说明。
(1)有符号
对于负数的下限,最高位作为符号位位1,用1 1 1 1 1 1 1 1,如图1所示。即为-127,而不是-128,
难道是1 0 0 0 0 0 0 0?其实就是用1 0 0 0 0 0 0 0表示-128的。以下进行说明。
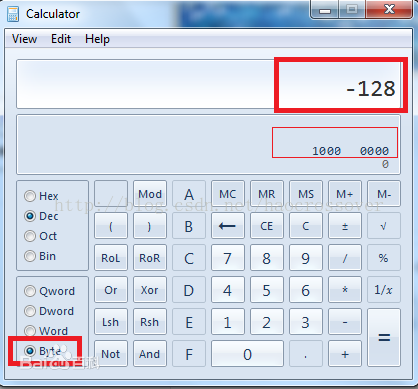
注意:1000 0000 B 不等于0 而是 -128(图2)
+127 +1 = -128
即 0111 1111 B+1 = 1000 0000 B
也就是发生了 byte值溢出
8位二进制反码的表示范围:-127~+127
为什么 -128 的二进制会是1000 0000;
1000 0000 (原) = 1111 1111(反)
那么问题来了: 64+32+16+8+4+2+1 = 127 为什么会有128呢?
原来 负数 反码是需要补码的,也就是在最后得出的结果上 +1
注意:计算机中只有 +0 而不存在 -0的说法,因为-0是完全没有意义的存在(见下对正0负0的说明),
即:只有 0000 0000 = +0
而没有 1000 0000 = -0
1000 0000的真实身份是 -128
图2
需要了解计算机对数据的存储表示方法(原码、反码、补码),以及负0与正零的表示。
(1)所谓原码就是前面所介绍的二进制定点表示法,即最高位为符号位,“0”表示正,“1”表示负,其余位表示数值的大小。
反码表示法规定:正数的反码与其原码相同;负数的反码是对其原码逐位取反,但符号位除外。
补码表示法规定:正数的补码与其原码相同;负数的补码是在其反码的末位加1。
原码不能直接参加运算,可能会出错。例如数学上,1+(-1)=0,而在二进制中00000001+10000001=10000010,换算成十进制为-2。显然出错了。所以原码的符号位不能直接参与运算,必须和其他位分开,这就增加了硬件的开销和复杂性。为了解决原码做减法的问题,出现了反码:计算十进制的表达式: 1-1=01 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原=[0000 0001]反 + [1111 1110]反 =[1111 1111]反 = [1000 0000]原 =-0 发现用反码计算减法, 结果的真值部分是正确的. 。而唯一的问题其实就出现在"0"这个特殊的数值上.虽然人们理解上+0和-0是一样的。但是0带符号是没有任何意义的.而且会有[0000 0000]原和[10000000]原两个编码表示0.于是补码的出现,
反码是数值存储的一种,多应用于系统环境设置,如linux平台的目录和文件的默认权限的设置umask,就是使用反码原理。
在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统一处理;同时,加法和减法也可以统一处理。此外,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路。负数的补码则是符号位为“1”。并且,这个“1”既是符号位,也是数值位。数值部分按位取反后再在末位(最低位)加1。也就是“反码+1”。
补码的出现,解决了0的符号以及两个编码的问题:1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 =[0000 0001]补 + [1111 1111]补 =[0000 0000]补=[0000 0000]原 ,这样0用[0000 0000]表示,而以前出现问题的-0则不存在了.而且可以用[10000000]表示-128:(-1) + (-127) = [1000 0001]原 + [1111 1111]原 =[1111 1111]补 + [1000 0001]补 =[1000 0000]补
-1-127的结果应该是-128,在用补码运算的结果中, [1000 0000]补 就是-128.但是注意因为实际上是使用以前的-0的补码来表示-128,所以-128并没有原码和反码表示.(对-128的补码表示[10000000]补算出来的原码是[0000 0000]原,这是不正确的)使用补码, 不仅仅修复了0的符号以及存在两个编码的问题,而且还能够多表示一个最低数.
这就是为什么8位二进制,使用原码或反码表示的范围为[-127, +127],而使用补码表示的范围为[-128, 127].因为机器使用补码,所以对于编程中常用到的32位int类型,可以表示范围是: [-2^31, 2^31-1]因为第一位表示的是符号位.而使用补码表示时又可以多保存一个最小值.
(2)根据原码的定义:正零和负零的原码为:
+0 : 0000 0000 0000 0000 0000 0000 0000 0000 (32 bit)
-0 : 1000 0000 0000 0000 0000 0000 0000 0000
而反码为:
+0 : 0000 0000 0000 0000 0000 0000 0000 0000
-0 : 1111 1111 1111 1111 1111 1111 1111 1111
补码为:
+0 : 0000 0000 0000 0000 0000 0000 0000 0000
-0 : 1 0000 0000 0000 0000 0000 0000 0000 0000
可以看出,-0的补码发生溢出,舍弃最高位后,其跟+0在内存的表示一样,都是:
0000 0000 0000 0000 0000 0000 0000 0000
再看看下面的图中所示错误。这个错误牵扯到一个叫模的概念。下面是解释。
1)模的概念:把一个计量单位称之为模或模数。例如,时钟是以12进制进行计数循环的,即以12为模。在时钟上,时针加上(正拨)12的整数位或减去(反拨)12的整数位,时针的位置不变。14点钟在舍去模12后,成为(下午)2点钟(14=14-12=2)。从0点出发逆时针拨10格即减去10小时,也可看成从0点出发顺时针拨2格(加上2小时),即2点(0-10=-10=-10+12=2)。因此,在模12的前提下,-10可映射为+2。由此可见,对于一个模数为12的循环系统来说,加2和减10的效果是一样的;因此,在以12为模的系统中,凡是减10的运算都可以用加2来代替,这就把减法问题转化成加法问题了(注:计算机的硬件结构中只有加法器,所以大部分的运算都必须最终转换为加法)。10和2对模12而言互为补数。
同理,计算机的运算部件与寄存器都有一定字长的限制(假设字长为8),因此它的运算也是一种模运算。当计数器计满8位也就是256个数后会产生溢出,又从头开始计数。产生溢出的量就是计数器的模,显然,8位二进制数,它的模数为2^8=256。在计算中,两个互补的数称为“补码”。
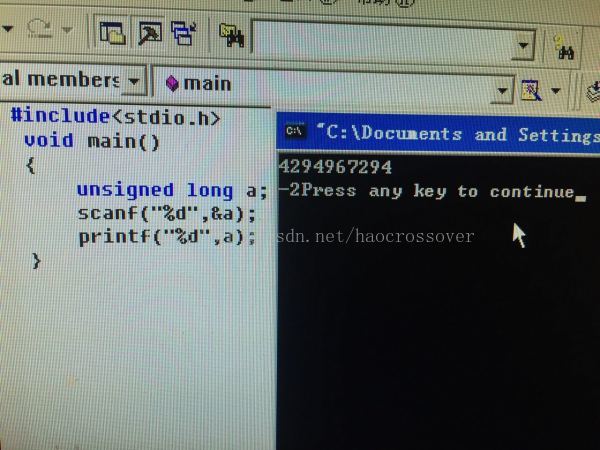
图3中 的错误解释:由于usigned long最大取值范围为2^32-1,而%d是以有符号整数进行输出,故进行了数值转换,即转为signed int,对于signed int 取值范围最大值小于usigned long,发生溢出,根据上述对模概念的说明,应该明白为什么输出是-2了。
图3
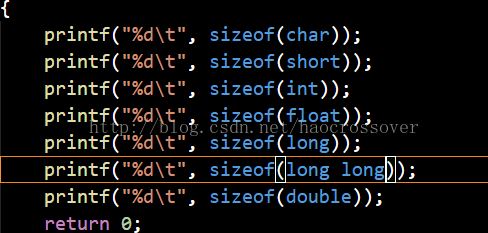
图4、图5为用基于X64处理器的gcc编译器输出各整型数据类型长度的结果
图4
图5






















 5274
5274

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








