介绍
对于Hissian矩阵是正定的,在这一点是整个范围内的最小值,y在各个方向的二阶导数都是>0的
对于Hissian矩阵是负定的,在这一点是整个范围内的最大值,y在各个方向的二阶导数都是<0的,
对于Hissian矩阵是不定的,y沿某些方向是上升的,沿另一些方向是下降的
对于有条件的极值,用拉格朗日乘数法
多元函数
从整个范围来看,不是单单从某个方向来看是否连续
偏导数
各个方向的偏导都存在,不一定连续,在点处极限不存在
方向导数
方向导数
当偏导数>0时,方向导数可以是正的,可以是负的
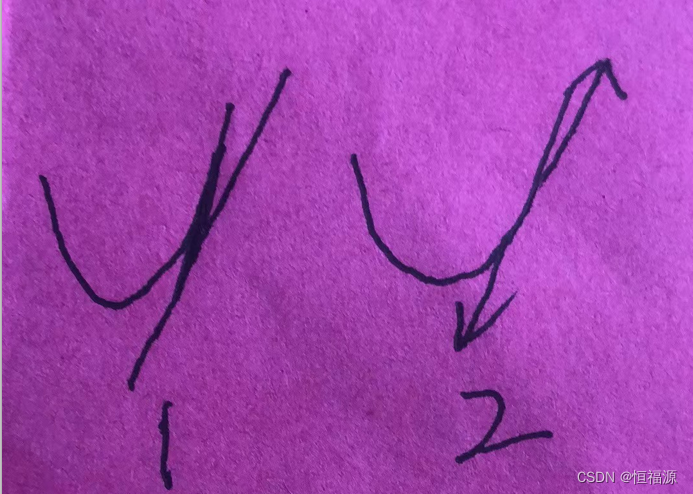
图1的斜线是偏导数,在图示点处,沿着x轴正方向走,偏导数是正的,沿着x轴负方向走,偏导数是负的,图2的斜线的正向或负向是方向导数
课程中最后无论从x轴正方向还是负方向走,都是1,有偏导数的话负方向应该是-1,所以没有偏导数
可微
函数在个方向上的变化用偏导数和方向导数不足以描述
在每一个方向的偏导数都连续,可微,偏导说的是某一个方向上的变化率,可微说的是在n个方向上的变化率加和,
梯度
在一个点处可微,梯度可以控制在各个方向上的变化率,梯度是f沿着各个方向上的变化。
Jacobi矩阵,是函数矩阵,各个函数的梯度组成的矩阵,在多元函数的积分和对应的行列式中用的比较多,
梯度,grad, grad(f+g)=grad(f)*f+grad(g)*f
链式法则
Hissian矩阵
f(x_0,x_1,…,x_n)在向量x_0处取极值,梯度在向量x_0处是0向量。
梯度在向量x_0处是0向量,可能是驻点
拉格朗日乘数法
隐函数定理
拉格朗日乘数法举例:
f(x,y,z)=x2+y2+z2
约束条件:g_1(x,y,z)=x+y+z-1=c1
g_2(x,y,z)=x-y=c2
拉格朗日函数为:
L(x,y,z, λ1, λ2)=f(x,y,z)- λ1(g_1(x,y,z)-c1)-λ2(g_2(x,y,z)-c2)
=x2+y2+z2-λ1(x+y+z-1-c1)-λ2(x-y-c2)
x,y,z为实数,c1,c2为常数,这里假设c1,c2都为0
= x^2 + y^2 + z^2 - λ1(x + y + z - 1) - λ2(x - y)
然后,对L(x, y, z, λ1, λ2)分别对x、y、z、λ1和λ2求偏导,并令它们等于零:
∂L/∂x = 2x - λ1 - λ2 = 0
∂L/∂y = 2y - λ1 + λ2 = 0
∂L/∂z = 2z - λ1 = 0
∂L/∂λ1 = -(x + y + z - 1) = 0
∂L/∂λ2 = -(x - y) = 0
解上述方程组,我们可以得到以下结果:
x = 1/2
y = 1/4
z = 1/4
λ1 = 3/2
λ2 = 1/2
因此,该三元函数在约束条件下的最大值为:
f(1/2, 1/4, 1/4) = (1/2)^2 + (1/4)^2 + (1/4)^2 = 5/16
这里,λ1和λ2的值分别为3/2和1/2,表示在两个约束条件下,目标函数最大值的增加速度为正。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








