数据结构篇--二项队列

什么是二项树？

递归定义

• 基础情形：阶数为0的二项树，仅包含一个节点；
• 构造情形：阶数为k的二项树，由两个阶数为k-1的二项树构造形成，即其中一个二项树的根作为另一个二项树的根的最左孩子节点。

下面分别是0阶、1阶、2阶、3阶二项树的构造示例。

什么是二的幂次堆？

定义
A power-of-2 heap is a left-heap-ordered tree consisting of a root node with an empty right subtree and a complete left subtree.

一个二的幂次堆是一棵左堆序树，它的根节点有一棵空的右子树、一棵完全左子树。

解读：

• 结构：它的根节点有一颗空的右子树，和一颗完全左子树。
• 它是左堆序的，这意味着：它的每个节点的键值大于等于左子树中所有节点的键值。
• 等价性：一个二的幂次堆一一对应一个二项树。

下面给出2的0次幂堆、2的1次幂堆、2的2次幂堆、2的3次幂堆的示例。

为什么一个二次幂堆对应一个二项树？

答：从二项树的根节点出发，从上到下，从左到右，依次遍历每个节点。对每个节点来说，如果它有左孩子，则左孩子就是它的左孩子节点。如果它有右兄弟，则这个右兄弟就作为它的右孩子节点。

什么是二项队列？

定义
A binomial queue is a set of power-of-2 heaps, no two of the same size.
The structure of a binomial queue is determined by that queue’s number of nodes, by correspondence with the binary representation of integers.

一个二项队列是一组二的幂次堆，其中没有两个二的幂次堆有相同的大小。
一个二项队列的结构是由该队列的节点数确定的，对应于该节点数的二进制表示。

解释

• 组成
• 唯一性
• 结构跟节点数的关系

如何表示一个二项队列？

• 使用数组来存储每个二次幂堆的入口，即根节点的引用。
• 数组的大小完全由二项队列的节点数的二进制表示的位数确定。
• 给定二项队列的节点数的二进制表示，其中的1表示该位置上有1个二次幂堆，0表示没有。

下面给出一个节点数为13的二项堆的示例。

实现二项队列

我们旨在实现优先级队列接口PQfull.h。

我们用来实现二项队列的框架代码

• Makefile
• PQfull.h
• Item.h
• BinomialQueue.c
• TestBinomialQueue.c

Makefile

CC = gcc
CFLAGS = -O0

TestBinomialQueue: TestBinomialQueue.c BinomialQueue.c
    $(CC) $(CFLAGS) -o $@ $^

clean:
    rm -f avg TestBinomialQueue

PQfull.h

/**
* FileName: PQfull.h
* ----------------------------------------------
* First-class priority-queue ADT
* ----------------------------------------------
* This interface for a priority-queue ADT provides
* - handles to items (which allow client programs to delete items and to change priorities) and
* - handles to priority queues (which allow clients to maintain multiple priority queues and to merge queues together).
*
* These types, `PQlink` and `PQ` respectively, are pointers to structures that are to * be specified in the implementation.
 */

#ifndef PQFULL_H
#define PQFULL_H

#include "Item.h"

typedef struct pq* PQ;
typedef struct PQnode* PQlink;

PQ PQinit();
int PQempty(PQ);
PQlink PQinsert(PQ, Item);
Item PQdelmax(PQ);
void PQchange(PQ, PQlink, Item);
void PQdelete(PQ, PQlink);
void PQjoin(PQ, PQ);

#endif //PQFULL_H

Item.h

#ifndef ITEM_H
#define ITEM_H

typedef char Item;

#define key(A) (A)
#define less(A,B) (key(A) < key(B))
#define exch(A, B) { Item t = A; A = B; B = t; }

#endif //ITEM_H

BinomialQueue.c

/**
 * FileName:BinomialQueue.c
 * ---------------------------------
 */

#include "PQfull.h"
#include <stddef.h>

struct PQnode {
    Item key;
    PQlink l;
    PQlink r;
    PQlink p;
};

struct pq{
    PQlink *bq;
};

#define maxBQsize 5

static PQlink z = NULL;

/******************************辅助函数部分开始************************************/

/******************************辅助函数部分结束************************************/

/******************************接口实现部分开始************************************/
PQ PQinit(){
    //TODO
}

int PQempty(PQ pq){
    //TODO
}

PQlink PQinsert(PQ pq, Item v){
    //TODO
}

Item PQdelmax(PQ pq){
    //TODO
}

void PQchange(PQ pq, PQlink x, Item v){
    //TODO
}

void PQdelete(PQ, PQlink){
    //TODO
}

void PQjoin(PQ a, PQ b){
    //TODO
}

/******************************接口实现部分结束************************************/

TestBinomialQueue.c

/**
 * FileName:TestBinomialQueue.c
 * ---------------------------------
 */

#include "PQfull.h"
 
void test_join();
void test_insert();
void test_delmax();
void test_change();
void test_delete();

int main(){
    return 0;
}

void test_join(){
    //TODO
}
void test_insert(){
    //TODO
}
void test_delmax(){
    //TODO
}
void test_change(){
    //TODO
}
void test_delete(){
    //TODO
}

如何运行测试代码？

#编译
make TestBinomialQueue
#运行
./TestBinomialQueue
#清理文件
make clean

本次实验总共有5个任务，分别是：

• PQjoin
• PQinsert
• PQdelmax
• PQchange
• PQdelete

因为可以使用PQjoin操作来实现PQinsert操作、PQdelmax操作，所以先来实现PQjoin操作。

因为可以通过调用PQchange来修改待删除节点的优先级为最大，然后调用PQdelmax操作来实现PQdelete操作，所以PQdelete操作的实现放在最后。

任务1：实现PQjoin操作

实现思路：类比1位二进制加法的操作来实现join操作。

首先，搞清楚一位二进制加法的操作都有哪些。

值	CBA	求和位	进位
0	000	0	0
1	001	1	0
2	010	1	0
3	011	0	1
4	100	1	0
5	101	0	1
6	110	0	1
7	111	1	1

接着，实现PQjoin。

void PQjoin(PQ a, PQ b){
    BQjoin(a->bq, b->bq);
}

#define test(C, B, A) 4*(C) + 2*(B) + 1*(A)
/**
 * 从右向左，依次处理每一个二次幂堆
 * -----------------------------
 * 思路：参考单比特的二进制加法操作
 */
void BQjoin(PQlink *a, PQlink *b){
    int i;
    PQlink c = z;
    for (i = 0; i < maxBQsize; i++) {
        switch(test(c != z, b[i] != z, a[i] != z)){
            case 2:
                a[i] = b[i];
                break;
            case 3:
                c = pair(a[i], b[i]);
                a[i] = z;
                break;
            case 4:
                a[i] = c;
                c = z;
                break;
            case 5:
                c = pair(c, a[i]);
                a[i] = z;
                break;
            case 6:
            case 7:
                c = pair(c, b[i]);
                break;
        }
    }
}

/**
 * 合并两个相同大小的二次幂堆
 * ----------------------------
 * 思路：TODO
 */
PQlink pair(PQlink p, PQlink q){
    if (less(p->key, q->key)) {
        p->r = q->l;
        if (p->r != z) {
            p->r->p = p;
        }
        q->l = p;
        p->p = q;
        return q;
    }else {
        q->r = p->l;
        if (q->r != z) {
            q->r->p = q;
        }
        p->l = q;
        q->p = p;
        return p;
    }
}

任务2：实现PQinsert操作

实现思路：类似于让一个二进制数跟1做加法
请注意：让这个1对应一个二的0幂次堆

PQlink PQinsert(PQ pq, Item v){
    PQlink t = malloc(sizeof(*t));
    t->key = v;
    t->l = z;
    t->r = z;
    t->p = z;
    PQ tempPQ = PQinit();
    tempPQ->bq[0] = t;

    PQjoin(pq, tempPQ);
    return t;
}

测试PQjoin

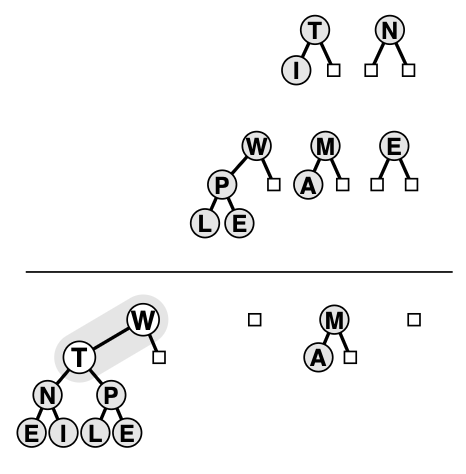
void test_join(){
    // 队列1：I->T->N
    PQ pq1 = PQinit();
    PQinsert(pq1, 'I');
    PQinsert(pq1, 'T');
    PQinsert(pq1, 'N');
    assert(pq1->bq[0]->key == 'N');
    assert(pq1->bq[1]->key == 'T');
    assert(pq1->bq[1]->l->key == 'I');

    // 队列2： P->L->E->W->M->A->E
    PQ pq2 = PQinit();
    PQinsert(pq2, 'P');
    PQinsert(pq2, 'L');
    PQinsert(pq2, 'E');
    PQinsert(pq2, 'W');
    PQinsert(pq2, 'M');
    PQinsert(pq2, 'A');
    PQinsert(pq2, 'E');
    assert(pq2->bq[0]->key == 'E');
    assert(pq2->bq[1]->key == 'M');
    assert(pq2->bq[1]->l->key == 'A');
    assert(pq2->bq[1]->r == z);
    assert(pq2->bq[2]->key == 'W');
    assert(pq2->bq[2]->r == z);
    assert(pq2->bq[2]->l->key == 'P');
    assert(pq2->bq[2]->l->r->key == 'E');
    assert(pq2->bq[2]->l->l->key == 'L');

    PQjoin(pq2, pq1);
    assert(pq2->bq[0] == z);
    assert(pq2->bq[1]->key == 'M');
    assert(pq2->bq[1]->l->key == 'A');
    assert(pq2->bq[2] == z);
    assert(pq2->bq[3]->key == 'W');
    assert(pq2->bq[3]->r == z);
    assert(pq2->bq[3]->l->key == 'T');
    assert(pq2->bq[3]->l->l->key == 'N');
    assert(pq2->bq[3]->l->r->key == 'P');
    assert(pq2->bq[3]->l->l->l->key == 'E');
    assert(pq2->bq[3]->l->l->r->key == 'I');
    assert(pq2->bq[3]->l->r->l->key == 'L');
    assert(pq2->bq[3]->l->r->r->key == 'E');
}

测试PQinsert

//向已有二项队列中插入节点N
void test_insert(){
    PQ pq = PQinit();
    // P-L-E-W-T-I-E
    PQinsert(pq, 'P');
    PQinsert(pq, 'L');
    PQinsert(pq, 'E');
    PQinsert(pq, 'W');
    PQinsert(pq, 'T');
    PQinsert(pq, 'I');
    PQinsert(pq, 'E');
    // N
    PQinsert(pq, 'N');

    assert(pq->bq[0] == z);
    assert(pq->bq[1] == z);
    assert(pq->bq[2] == z);
    assert(pq->bq[3]->key == 'W');
    assert(pq->bq[3]->r == z);
    assert(pq->bq[3]->l->key == 'T');
    assert(pq->bq[3]->l->l->key == 'N');
    assert(pq->bq[3]->l->r->key == 'P');
    assert(pq->bq[3]->l->l->l->key == 'E');
    assert(pq->bq[3]->l->l->r->key == 'I');
    assert(pq->bq[3]->l->r->l->key == 'L');
    assert(pq->bq[3]->l->r->r->key == 'E');
}

任务3：实现PQdelmax操作

Item PQdelmax(PQ pq){
    int i;
    int max;
    Item v;
    PQlink x;
    PQlink temp[maxBQsize];


    for (i = 0, max = -1; i < maxBQsize; i++) {
        if (pq->bq[i] != z) {
            if (max == -1 || less(v, pq->bq[i]->key)) {
                max = i;
                v = pq->bq[i]->key;
            }
        }
    }
    for (i = max; i < maxBQsize; i++) {
        temp[i] = z;
    }
    x = pq->bq[max]->l;
    for (i = max; i > 0; i--) {
        temp[i-1] = x;
        x = x->r;
        temp[i-1]->r = z;
    }
    free(pq->bq[max]);
    pq->bq[max] = z;

    BQjoin(pq->bq, temp);

    return v;

}

测试PQdelmax

void test_delmax() {
    PQ pq = PQinit();
    PQinsert(pq, 'A');
    PQinsert(pq, 'S');
    PQinsert(pq, 'O');
    PQinsert(pq, 'R');
    PQinsert(pq, 'T');
    PQinsert(pq, 'I');
    PQinsert(pq, 'N');
    PQinsert(pq, 'G');
    PQinsert(pq, 'E');
    PQinsert(pq, 'X');
    PQinsert(pq, 'A');
    PQinsert(pq, 'M');
    PQinsert(pq, 'P');
    PQinsert(pq, 'L');
    PQinsert(pq, 'E');
    PQinsert(pq, 'W');

    assert(pq->bq[0] == z);
    assert(pq->bq[1] == z);
    assert(pq->bq[2] == z);
    assert(pq->bq[3] == z);
    assert(pq->bq[4]->key == 'X');

    PQdelmax(pq);
    assert(pq->bq[0]->key == 'E');
    assert(pq->bq[1]->key == 'M');
    assert(pq->bq[2]->key == 'W');
    assert(pq->bq[3]->key == 'T');


}

任务4：实现PQchange操作

void fixUp(PQlink x){
    PQlink curr = x;
    while (curr != z && curr->p != z && less(curr->p->key, curr->key)) {
        exch(curr->key, curr->p->key);
        curr = curr->p;
    }
}

void fixDown(PQlink x){
    PQlink curr = x;
    while (curr != z) {
        PQlink max_child = z;
        PQlink child_iter = curr->l;
        while(child_iter != z){
            if (max_child == z || less(max_child->key, child_iter->key)) {
                max_child = child_iter;
            }
            child_iter = child_iter->r;
        }
        if (max_child == z || max_child->key <= curr->key) {
            break;
        }
        exch(max_child->key, curr->key);
        curr = max_child;
    }
}

void PQchange(PQ pq, PQlink x, Item v){
    if (x == z) {
        return;
    }
    
    Item old = x->key;
    x->key = v;
    
    if (less(old, v)) {
        fixUp(x);
    }else {
        fixDown(x);
    }
}

测试PQchange

void test_change(){
    PQ pq = PQinit();
    // E-A-S-Y-Q-U-E-S-T-I-O-N
    PQinsert(pq, 'E');
    PQinsert(pq, 'A');
    PQinsert(pq, 'S');
    PQlink x = PQinsert(pq, 'Y');
    PQinsert(pq, 'Q');
    PQinsert(pq, 'U');
    PQinsert(pq, 'E');
    PQinsert(pq, 'S');
    PQinsert(pq, 'T');
    PQinsert(pq, 'I');
    PQinsert(pq, 'O');
    PQinsert(pq, 'N');

    PQchange(pq, x, 'B');

    assert(pq->bq[3]->key == 'U');
    assert(pq->bq[3]->l->key == 'S');
    assert(pq->bq[3]->l->l->key == 'E');
    assert(pq->bq[3]->l->l->l->key == 'B');
}

任务5：实现PQdelete操作

#define MAXCHAR 127
void PQdelete(PQ pq, PQlink x){
    PQchange(pq, x, MAXCHAR);
    PQdelmax(pq);
}

测试PQdelete

void test_delete() {
    PQ pq = PQinit();
    // E-A-S-Y-Q-U-E-S-T-I-O-N
    PQinsert(pq, 'E');
    PQinsert(pq, 'A');
    PQinsert(pq, 'S');
    PQinsert(pq, 'Y');
    PQinsert(pq, 'Q');
    PQinsert(pq, 'U');
    PQinsert(pq, 'E');
    PQinsert(pq, 'S');
    PQinsert(pq, 'T');
    PQlink del = PQinsert(pq, 'I');
    PQinsert(pq, 'O');
    PQinsert(pq, 'N');

    PQdelete(pq, del);

    assert(pq->bq[0]->key == 'O');
    assert(pq->bq[1]->key == 'T');
    assert(pq->bq[1]->l->key == 'N');
    assert(pq->bq[2] == z);
}

参考资料

• BinomialQueue.c

  /**
   * FileName:BinomialQueue.c
   * ---------------------------
   *
   */
  
  #include <stdlib.h>
  #include "PQfull.h"
  
  #define test(C, B, A) 4*(C) + 2*(B) + 1*(A)
  #define maxBQsize 5
  #define MAXCHAR 127
  
  /******************************辅助函数部分开始************************************/
  /**
   * 合并两个相同大小的二次幂堆
   * ----------------------------
   * 思路：TODO
   */
  PQlink pair(PQlink p, PQlink q){
      if (less(p->key, q->key)) {
          p->r = q->l;
          if (p->r != z) {
              p->r->p = p;
          }
          q->l = p;
          p->p = q;
          return q;
      }else {
          q->r = p->l;
          if (q->r != z) {
              q->r->p = q;
          }
          p->l = q;
          q->p = p;
          return p;
      }
  }
  
  /**
   * 从右向左，依次处理每一个二次幂堆
   * -----------------------------
   * 思路：参考单比特的二进制加法操作
   */
  void BQjoin(PQlink *a, PQlink *b){
      int i;
      PQlink c = z;
      for (i = 0; i < maxBQsize; i++) {
          switch(test(c != z, b[i] != z, a[i] != z)){
              case 2:
                  a[i] = b[i];
                  break;
              case 3:
                  c = pair(a[i], b[i]);
                  a[i] = z;
                  break;
              case 4:
                  a[i] = c;
                  c = z;
                  break;
              case 5:
                  c = pair(c, a[i]);
                  a[i] = z;
                  break;
              case 6:
              case 7:
                  c = pair(c, b[i]);
                  break;
          }
      }
  }
  
  void fixUp(PQlink x){
      PQlink curr = x;
      while (curr != z && curr->p != z && less(curr->p->key, curr->key)) {
          exch(curr->key, curr->p->key);
          curr = curr->p;
      }
  }
  
  void fixDown(PQlink x){
      PQlink curr = x;
      while (curr != z) {
          PQlink max_child = z;
          PQlink child_iter = curr->l;
          while(child_iter != z){
              if (max_child == z || less(max_child->key, child_iter->key)) {
                  max_child = child_iter;
              }
              child_iter = child_iter->r;
          }
          if (max_child == z || max_child->key <= curr->key) {
              break;
          }
          exch(max_child->key, curr->key);
          curr = max_child;
      }
  }
  /******************************辅助函数部分结束************************************/
  
  /******************************接口实现部分开始************************************/
  
  PQ PQinit(){
      PQ pq = malloc(sizeof(*pq));
      pq->bq = (PQlink *)malloc(maxBQsize*sizeof(PQlink));
      int i;
      for (i = 0; i < maxBQsize; i++) {
          pq->bq[i] = z;
      }
      return pq;
  }
  
  int PQempty(PQ pq){
      //TODO
  }
  
  PQlink PQinsert(PQ pq, Item v){
      PQlink t = malloc(sizeof(*t));
      t->key = v;
      t->l = z;
      t->r = z;
      t->p = z;
      PQ tempPQ = PQinit();
      tempPQ->bq[0] = t;
  
      PQjoin(pq, tempPQ);
      return t;
  }
  
  Item PQdelmax(PQ pq){
      int i;
      int max;
      Item v;
      PQlink x;
      PQlink temp[maxBQsize];
  
  
      for (i = 0, max = -1; i < maxBQsize; i++) {
          if (pq->bq[i] != z) {
              if (max == -1 || less(v, pq->bq[i]->key)) {
                  max = i;
                  v = pq->bq[i]->key;
              }
          }
      }
      for (i = max; i < maxBQsize; i++) {
          temp[i] = z;
      }
      x = pq->bq[max]->l;
      for (i = max; i > 0; i--) {
          temp[i-1] = x;
          x = x->r;
          temp[i-1]->r = z;
      }
      free(pq->bq[max]);
      pq->bq[max] = z;
  
      BQjoin(pq->bq, temp);
  
      return v;
  
  }
  
  void PQchange(PQ pq, PQlink x, Item v){
      if (x == z) {
          return;
      }
  
      Item old = x->key;
      x->key = v;
  
      if (less(old, v)) {
          fixUp(x);
      }else {
          fixDown(x);
      }
  }
  
  void PQdelete(PQ pq, PQlink x){
      PQchange(pq, x, MAXCHAR);
      PQdelmax(pq);
  }
  
  void PQjoin(PQ a, PQ b){
      BQjoin(a->bq, b->bq);
  }
  
  /******************************接口实现部分结束************************************/
  

• TestBinomialQueue.c

  /**
   * FileName:TestBinomialQueue.c
   * ---------------------------------
   */
  
  #include <assert.h>
  #include "PQfull.h"
  
  void test_join();
  void test_insert();
  void test_delmax();
  void test_change();
  void test_delete();
  
  int main(){
      // test_join();
      // test_insert();
      // test_delmax();
      // test_change();
      test_delete();
      return 0;
  }
  
  void test_join(){
      // 队列1：I->T->N
      PQ pq1 = PQinit();
      PQinsert(pq1, 'I');
      PQinsert(pq1, 'T');
      PQinsert(pq1, 'N');
      assert(pq1->bq[0]->key == 'N');
      assert(pq1->bq[1]->key == 'T');
      assert(pq1->bq[1]->l->key == 'I');
  
      // 队列2： P->L->E->W->M->A->E
      PQ pq2 = PQinit();
      PQinsert(pq2, 'P');
      PQinsert(pq2, 'L');
      PQinsert(pq2, 'E');
      PQinsert(pq2, 'W');
      PQinsert(pq2, 'M');
      PQinsert(pq2, 'A');
      PQinsert(pq2, 'E');
      assert(pq2->bq[0]->key == 'E');
      assert(pq2->bq[1]->key == 'M');
      assert(pq2->bq[1]->l->key == 'A');
      assert(pq2->bq[1]->r == z);
      assert(pq2->bq[2]->key == 'W');
      assert(pq2->bq[2]->r == z);
      assert(pq2->bq[2]->l->key == 'P');
      assert(pq2->bq[2]->l->r->key == 'E');
      assert(pq2->bq[2]->l->l->key == 'L');
  
      PQjoin(pq2, pq1);
      assert(pq2->bq[0] == z);
      assert(pq2->bq[1]->key == 'M');
      assert(pq2->bq[1]->l->key == 'A');
      assert(pq2->bq[2] == z);
      assert(pq2->bq[3]->key == 'W');
      assert(pq2->bq[3]->r == z);
      assert(pq2->bq[3]->l->key == 'T');
      assert(pq2->bq[3]->l->l->key == 'N');
      assert(pq2->bq[3]->l->r->key == 'P');
      assert(pq2->bq[3]->l->l->l->key == 'E');
      assert(pq2->bq[3]->l->l->r->key == 'I');
      assert(pq2->bq[3]->l->r->l->key == 'L');
      assert(pq2->bq[3]->l->r->r->key == 'E');
  
  
  }
  
  void test_insert(){
      PQ pq = PQinit();
      // P-L-E-W-T-I-E
      PQinsert(pq, 'P');
      PQinsert(pq, 'L');
      PQinsert(pq, 'E');
      PQinsert(pq, 'W');
      PQinsert(pq, 'T');
      PQinsert(pq, 'I');
      PQinsert(pq, 'E');
      // N
      PQinsert(pq, 'N');
  
      assert(pq->bq[0] == z);
      assert(pq->bq[1] == z);
      assert(pq->bq[2] == z);
      assert(pq->bq[3]->key == 'W');
      assert(pq->bq[3]->r == z);
      assert(pq->bq[3]->l->key == 'T');
      assert(pq->bq[3]->l->l->key == 'N');
      assert(pq->bq[3]->l->r->key == 'P');
      assert(pq->bq[3]->l->l->l->key == 'E');
      assert(pq->bq[3]->l->l->r->key == 'I');
      assert(pq->bq[3]->l->r->l->key == 'L');
      assert(pq->bq[3]->l->r->r->key == 'E');
  }
  
  void test_delmax() {
      PQ pq = PQinit();
      PQinsert(pq, 'A');
      PQinsert(pq, 'S');
      PQinsert(pq, 'O');
      PQinsert(pq, 'R');
      PQinsert(pq, 'T');
      PQinsert(pq, 'I');
      PQinsert(pq, 'N');
      PQinsert(pq, 'G');
      PQinsert(pq, 'E');
      PQinsert(pq, 'X');
      PQinsert(pq, 'A');
      PQinsert(pq, 'M');
      PQinsert(pq, 'P');
      PQinsert(pq, 'L');
      PQinsert(pq, 'E');
      PQinsert(pq, 'W');
  
      assert(pq->bq[0] == z);
      assert(pq->bq[1] == z);
      assert(pq->bq[2] == z);
      assert(pq->bq[3] == z);
      assert(pq->bq[4]->key == 'X');
  
      PQdelmax(pq);
      assert(pq->bq[0]->key == 'E');
      assert(pq->bq[1]->key == 'M');
      assert(pq->bq[2]->key == 'W');
      assert(pq->bq[3]->key == 'T');
  
  
  }
  
  void test_change(){
      PQ pq = PQinit();
      // E-A-S-Y-Q-U-E-S-T-I-O-N
      PQinsert(pq, 'E');
      PQinsert(pq, 'A');
      PQinsert(pq, 'S');
      PQlink x = PQinsert(pq, 'Y');
      PQinsert(pq, 'Q');
      PQinsert(pq, 'U');
      PQinsert(pq, 'E');
      PQinsert(pq, 'S');
      PQinsert(pq, 'T');
      PQinsert(pq, 'I');
      PQinsert(pq, 'O');
      PQinsert(pq, 'N');
  
      PQchange(pq, x, 'B');
  
      assert(pq->bq[3]->key == 'U');
      assert(pq->bq[3]->l->key == 'S');
      assert(pq->bq[3]->l->l->key == 'E');
      assert(pq->bq[3]->l->l->l->key == 'B');
  }
  
  void test_delete() {
      PQ pq = PQinit();
      // E-A-S-Y-Q-U-E-S-T-I-O-N
      PQinsert(pq, 'E');
      PQinsert(pq, 'A');
      PQinsert(pq, 'S');
      PQinsert(pq, 'Y');
      PQinsert(pq, 'Q');
      PQinsert(pq, 'U');
      PQinsert(pq, 'E');
      PQinsert(pq, 'S');
      PQinsert(pq, 'T');
      PQlink del = PQinsert(pq, 'I');
      PQinsert(pq, 'O');
      PQinsert(pq, 'N');
  
      PQdelete(pq, del);
  
      assert(pq->bq[0]->key == 'O');
      assert(pq->bq[1]->key == 'T');
      assert(pq->bq[1]->l->key == 'N');
      assert(pq->bq[2] == z);
  }