KMP算法（The Knuth-Morris-Pratt Algorithm）

KMP算法详解（原理，实现，拓展）

前言

字符串匹配，一般来说是将模式串与主串进行比较，并返回第一次匹配成功模式串出现在主串中的位置。实现上，通过设置游标来逐个比较主串和模式串的字符，并使游标遵循特定的规则滑动。根据滑动规则的不同，衍生出各式各样的匹配算法。本篇讲诉的KMP算法就是其中一种。

原理（前篇）

简陋的匹配方式（plain match）

在开始KMP算法的原理前，需要稍微提一下一种最直观的匹配算法，这里称它为plain match。一次匹配成功或匹配失败都称作一轮匹配（注意：匹配针对的是串，比较针对的是字符，通常情况下，一次匹配包含了多次比较），则plain match的规则如下：当主串和模式串比较成功时，两者的游标都往后移一位，若模式串的游标达到末尾，则这完成一轮成功的匹配；当主串和模式串比较失败时，模式串的游标将重置（移动至串的开头），主串的游标将回溯（向前移动）至这一轮匹配起始位置的后一位，即完成一轮失败的匹配。

plain match的规则很简单，便于实现。时间复杂度为O(n * m)，其中n是主串的长度，m是模式串的长度，并且在实际执行中近似于O(n + m)，因此至今仍被采用。

plain match的问题

稍加分析会发现，plain match的规则存在一些问题。而且直觉会告诉我们，问题一定出现在主串游标的回溯上：似乎容易回溯得“过远”。假设主串为：acabaabaabcacaabc，模式串为abaabcac，两者的灰色部分比较结束后，比较下一个字符将导致一轮失败的匹配。根据规则，下一轮的匹配将是以这样一种形式开始：acabaabaabcacaabc的灰‘b’将与模式串的abaabcac灰‘a’展开比较。但是，最理想的方式应该是将主串的黄‘a’与模式串的黄‘a’作比较。由此可见，plain match确实存在主串游标回溯过远的问题。解决这个问题，将引入KMP算法。

改进plain match——KMP算法的第一个描述

KMP一个最大的特点，就是主串游标不需要回溯。这种改进在实际应用中有不错的优点，例如在读入输入的数据（主串）时，可以边读入边进行匹配。利用KMP算法，当出现匹配失败时，完全不需要回头重新读入（回溯的过程）。plain match自身的比较方式没有办法做这样的改进。于是，给出KMP算法的第一个描述：当主串和模式串比较成功时，两者的游标都往后移一位，若模式串的游标到达末尾，则完成一轮成功的匹配；当主串和模式串比较失败时，主串的游标不动，模式串的游标将回溯到一个“恰当的位置”，即完成一轮失败的匹配，下一轮将从两者游标所指开始。用形象的方式描述，就是在比较失败的时候，模式串将”向右滑动一段尽可能远的距离“来结束这一轮匹配（接下去的文章中会交替使用两种描述方式）。

但是，”恰当的位置“和”尽量能远的距离“都是非常模糊的描述，这种描述就跟讲诉plain match时的直观感觉一样，无法给出一个定量的结果。接下去就要直击KMP算法的命门，寻找实现理想的现实之门。

原理（中篇）

理想的位置——KMP算法的第二个描述

在开始前往理想的位置前回顾一下“plain match的问题”中的示例。acabaabaabcacaabc和abaabcac的灰色部分比较失败后，直观告诉我们理想的下一轮匹配将从acabaabaabcacaabc和abaabcac的黄色位置开始，原因就是abaab的前两个字符和末两个字符一样。滑动的过程就像下面这样：

• acabaabaabcacaabc  acabaabaabcacaabc  acabaabaabcacaabc  acabaabaabcacaabc  acabaabaabcacaabc  
• abaabcac                     abaabcac                    abaabcac                    abaabcac                     abaabcac                 

观察后能发现，实际上是在abaab这个串上做文章。我们来构造两个有趣的集合，问题就会清晰了。P={abaab，baab，aab，ab，b}和Q={abaab，abaa，aba，ab，a}。可以看出来，P和Q集合的元素都是abaab的子串。其中P是从最末一个字符开始逐个向前增加形成的子串集合，Q则是从第一个字符开始逐个向后增加形成的子串集合。绿色部分是两个集合的公共元素。这两个集合能够表征滑动过程中的状态，如果将它们视为数组，则滑动从P[0]、Q[0]开始，由P[3]、Q[3]结束，就像是这样:

以上就是KMP算法的第二个描述。任何一次比较失败后，构造两个状态集合P和Q。P与Q的交集Z中至少有一个元素，它是滑动开始时的状态（如示例中的abaab）。若Z中只含有一个元素，意味着开始状态即结束状态（就像是头尾相交）。若Z中有超过一个元素，则按顺序寻找下一个元素（如示例中的ab）作为滑动的结束状态。这里要注意的按顺序寻找下一个，这是必要的，因为这种方式能保证找到的结束状态总是正确的。以一个Z中包含四个元素的例子来说明按顺序寻找的必要性，同时结束这一部分。

exp. 主串：abaabaaabaaabaabba， 模式串：aabaaabaabba，黄色字符比较后失败，模式串开始滑动：

• abaabaaabaaabaabba  abaabaaabaaabaabba  abaabaaabaaabaabba  abaabaaabaaabaabba  abaabaaabaaabaabba  abaabaaabaaabaabba  abaabaaabaaabaabba  abaabaaabaaabaabba
• aabaaabaabba              aabaaabaabba               aabaaabaabba              aabaaabaabba               aabaaabaabba               aabaaabaabba              aabaaabaabba               aabaaabaabba

可求得两个状态集合，P={aabaaabaa，abaaabaa，baaabaa，aaabaa，aabaa，abaa，aa，a}，Q={aabaaabaa，aabaaaba，aabaaab，aabaaa，aabaa，aaba，aa，a}，以及它们的交集Z=P^Q={aabaaabaa，aabaa，aa，a}。按照KMP算法第二个描述的规则，将选取aabaa作为结束状态，则滑动后的情况如下：

• abaabaaabaaabaabba
•            aabaaabaabba

显然，下一轮将匹配成功，并且结束整个匹配过程。但是，若选取aa或是a作为结束状态，将漏掉一次成功的匹配，这是完全意义上的错误！选取较靠后的元素能让模式串滑动尽可能远的距离，但是，草率地排除前面的元素将导致不必要的风险。

轨迹——序列探索

集合Z中的每个元素都是P和Q的公共部分，如果说P和Q中的元素都是子串，那么Z中的便是公共子串，或者称作公共子序列。接下去的分析便从公共子序列着手，并且从更一般的情况来进行。

假设，字符序列S=s(1), s(2), s(3)...s(n)为主串，序列T=t(1), t(2), t(3)...t(m)为模式串，i和j分别为序列S和T的下标。于是，比较失败的情形可以描述为s(i) != t(j)。此时，通过集合Z的结束状态我们得到一个下标k，这个下标是下一轮匹配开始时序列T用于比较的字符的下标（串的游标和序列的下标可以认为是一致的，描述上不再细分）。如果用公共子序列来描述，就是这样：

• t(1), t(2)...t(k-1)  ==  s(i-k+1), s(i-k+2)...s(i-1)

而且，在比较失败时，我们已经有了一段公共子序列，如下：

• t(j-k+1), t(j-k+2)...t(j-1)  ==  s(i-k+1), s(i-k+2)...s(i-1)

于是，下面这个等式也是成立的：

• t(j-k+1), t(j-k+2)...t(j-1)  ==  t(1), t(2)...t(k-1) 

上面这个式子给出了和集合Z中每个结束状态唯一对应的下标k应满足的关系。同时，我们惊喜地发现，式子中不含i。这意味着，k仅仅和j有关，换句话说，k仅仅和模式串有关。这表明了，当比较失败时，通过模式串的游标位置和整个模式串的字符信息，可以求出k，进而构造出集合Z。这个等式是实现KMP算法的基石。

滑动——指向终点的next数组

在上一部分中，通过模式串和比较失败时得到的信息，求出了下标k和j的等式。因为k和i无关，于是在开始滑动前，甚至在第一轮匹配前，就可以将所有k值都计算出来。在之后的匹配过程中，若出现比较失败，则通过查找和j对应的k值来确定模式串应滑动到的位置。接下去，将引入一个称作next的数组，它的作用就是存放这些k值。显然，有next[j] == k

在这里，我们假设字符序列的下标从1开始。而通过等式可以看出，k的有效值域为{k| 1 < k < j}。在讲诉集合Z的部分中，曾提到了应当按顺序向后寻找下一个元素作为结束位置。这在我们构造的集合Z中意味着将是能保证最小滑动距离的元素，换句话说，需要的是一段最长的公共子序列。综合后，可以这样求next数组的元素：

• next[j] = MAX{k | 1<k<j  &&  t(j-k+1), t[j-k+2]...t[j-1]==t[1], t[2]...t[k-1]}，当然，这里的集合必须是非空的

当集合为空时，需要分两类情况讨论。

1. 当集合{k | 1 < k < j}为空时，即j == 1。我们可以设想，当模式串第一个字符就比较失败时，应该做什么？显然，应该保持j的值不动，然后让主串的游标向前滑动一位。但是为了和比较成功时游标的滑动情况做一个统一，我们把next[1]的值设为0。
2. 当集合{k | t(j-k+1), t[j-k+2]...t[j-1]==t[1], t[2]...t[k-1]}为空时，即没有任何公共子序列。此时，很自然的会让模式串的游标回溯到第一个字符的位置，即设k=1，来做一次“全新的比较”。（可以认为集合Z的最后一个元素是‘空’，当这里的情况出现时，那个‘空’就是结束状态。）

最后，做一下归纳：

1. 当集合非空时，next[j] = MAX{k | 1<k<j  &&  t(j-k+1), t[j-k+2]...t[j-1]==t[1], t[2]...t[k-1]}，
2. 当j == 1时，next[j] = 0
3. 其它情况，next[j] = 1

根据上面三条，还是不能机械地求出next数组中每一个元素的值，但已经足够通过手工的方式求出。在给出完全的求解方式前，我们先用手工的方式来生成一个next数组，并通过这个数组和C语言，来实现一段利用了KMP算法来进行字符串匹配的简单代码。

实现（1）

手工生成next数组

同样以plain match中的两个字符串为例（我觉得已经可以把它默出来了），主串：acabaabaabcacaabc，模式串abaabcac，接下去以手工方式来得到模式串的next数组：

1. 最简单的，next[1] = 0
2. j == 2时，{k | 1 < k < 2}为空，即next[2] = 1
3. j == 3时，k能取的值只有2，但是t[2] != t[1]，于是next[3] = 1
4. j == 4时，k能取的值有2和3，其中t[3] == t[1]，t[2]t[3] != t[1]t[2]，于是next[4] = 2
5. 同理，可以求得next[5] = 2，next[6] = 3，next[7] = 1，next[8] = 2

完整的模式串和next数组对应关系如下：

•          j              1  2  3  4  5  6  7  8
• pattern string   a  b  a  a  b  c  a  c
• next[ j ]            0  1  1  2  2  3  1  2

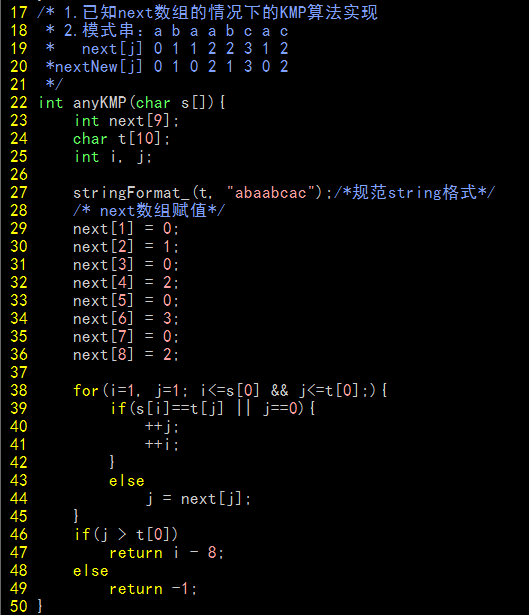
第一个KMP程序（C实现）

代码如下：

说明：

1. 这里有个stringFormat_函数，作用是规范string的格式，前文已经说明，文章中的字符序列下标均从1开始。
2. stringFormat_函数会将数组的第一个元素用于存储字符串的长度，因此在for-loop的判断部分运用了s[0]和t[0]（字符串长度）进行比较。
3. 最后，之前说将next[1]设为0将能和匹配成功时有统一的滑动行为，通过代码，应该更容易理解这句话的意思。

原理（后篇）

特殊情况下的数学归纳

在“原理中篇”的最后部分我们推导了三个等式，其中最后一个称作KMP算法的基石。通过这块基石，得到了比较粗糙的生成next数组的方式（手工）。对于比较短的模式串，即使用手工的方式也是可行的，但长度稍长之后，便会变得很复杂，而且容易出错。因此，如何以算法的形式来生成next数组是必要的。首先，通过计算机科学中最常用到的思维方式之一——数学归纳法来求出一些“特殊情况”下的next元素值。

重新回到对序列的分析上来。综合前面的分析，k == next[j]，等价于下面这个等式成立：

• t(j-k+1), t(j-k+2)...t(j-1)  ==  t(1), t(2)...t(k-1) 

那么，next数组下一个元素的值，即next[j+1]的值是多少呢？根据规则，下一次比较的是t[j+1]和s[i+1]，于是，上面等式左右两边的字符序列也自然地往后“发展一位”：

• t(j-k+1), t(j-k+2)...t(j-1), t(j)
• t(1), t(2)...t(k-1), t(k)

若t[k] == t[j]，则next[j+1] = k+1 = next[j] + 1，首尾部分构成规范的第一数学归纳法式子。而next[1] = 0是始终成立的，于是，通过数学归纳法可以求出所有next元素的值。但是，更多情况下，t[k] != t[j]，那么，要怎么解决这个问题呢？

next的next——KMP关键思想的再运用

当t[k] != t[j]时，模式串将继续向右滑动，直到出现一个k'，满足t[k'] == t[j]。似曾相识的一幕：

• 主串：       t(j-k+1), t(j-k+2)...t(j-1), t(j)
• 模式串：   t(1), t(2)...t(k-1), t(k)

没错，就是进行KMP算法出现比较失败时模式串的滑动。解决方法应运而生。next[k]的值指出了模式串滑动的位置，比较t[next[k]]和t[j]，相等则k' = next[k]，否则继续滑动，直到比较相等为止。若过程中到达了next[1]，表明不存在任何公共序列，对于整个序列T（模式串）和序列S（主串）的匹配来说，序列T所要做的就是开始一次全新的匹配，这意味着next[j+1] = 1。

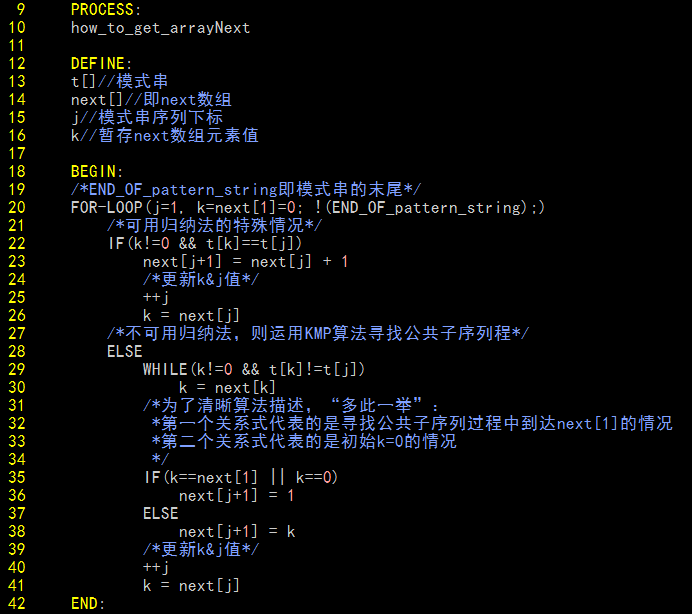
next算法，完成！

整理上面的思路，给出求next数组的完整算法（重点放在描述算法的逻辑思路）：

实现（2）

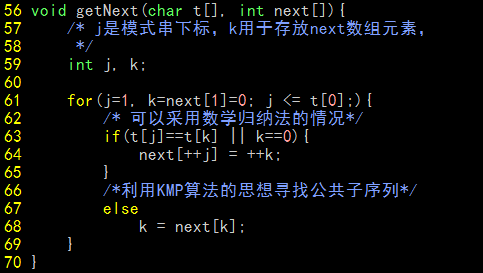
getNext函数（C实现）

同样使用C语言来实现生成next数组的函数。实现的根据就是上面描述的算法，再一次强调文章中所有字符序列（串）的下标都将从1开始，因此，实现时要注意next[1] = 0，而不是next[0] = 0。代码如下：

相比算法描述，代码实现上还是比较简洁的。最明显的是k == 0的所有情况都可以并到一起处理，同样还有++j的操作。

拓展

更理想的位置

我们要求的k值总是最大的一个，这在next[j] = MAX{k | 1<k<j  &&  t(j-k+1), t[j-k+2]...t[j-1]==t[1], t[2]...t[k-1]}中已经表现得很明显。前面也说明，之所以这么做遵从的是KMP算法第二个描述中的一条原则：“结束状态应当是Z集合按顺序寻找的下一个元素”。在当时，我们说明了这种方式能保证得到的结束状态都是“安全的”（不会遗漏成功的匹配），并且举了一个Z包含四个元素的例子来说明。接下来，将通过讨论一个运用KMP算法进行匹配的例子来重新审视这条原则。

exp. 主串：aaabaaaab，模式串：aaaab，i，j分别为主串和模式串序列的下标

首先来求模式串的next数组，如下：

•     j          1  2  3  4  5
• 模式串    a  a  a  a  b
• next[j]     0  1  2  3  4

接着来进行字符串的匹配。第一次失败时的情况如下：

• aaabaaaab
• aaaab

此时，j == 4，对应的next[4]值为3，滑动后的情况如下：

• aaabaaaab
•   aaaab

很遗憾，比较失败，此时j == 3，对应的next[3]值为2，滑动后的情况如下：

• aaabaaaab
•     aaaab

依然失败，此时j == 2，对应的next[2]值为1，滑动后的情况如下：

• aaabaaaab
•       aaaab

彻底失败，开始一次全新的匹配：

• aaabaaaab
•         aaaab

上面的匹配过程中，如果能在第一次失败后就直接滑动到最后一步的位置，就能减少很多不必要的匹配。那么，在这里，是否有通用的办法来做出判断呢，或者说，这个模式串本身又有着什么样的特点？

我们仔细看看上述的匹配过程。当第一次比较失败时，集合Z={aaa，aa，a}。我们选择aa作为第一次失败的结束状态，但是，新一轮开始比较的字符和上一轮中比较失败时的字符相等，这显然会导致失败匹配。接着，在第二次比较失败时，集合Z={aa，a}。我们选择a作为结束状态，同样的原因再一次导致失败匹配。到这里，已经很自然地得出结论：新一轮开始比较的字符和上一轮中比较失败的字符相等时，这样的状态不能作为真正的结束状态。

具体来说，当比较失败时，通过构造集合Z寻找到一个结束状态。通过结束状态得到下一轮开始比较的字符，此时，将该字符与刚刚比较失败的字符对照。

1. 若不相等，则表明这是真正的结束状态。
2. 否则，认为现在又出现了一次比较失败，并且就这个比较失败构造集合Z来继续寻找结束状态。

模式串的每个字符都对应着一个结束状态。可以假定，前面字符对应的都是真正的结束状态。因此，在情况2中，需要寻找的就是前面某个字符对应的结束状态。

序列描述

通过序列下标，再把上面这个过程描述一遍。和之前一样，假设，字符序列S=s(1), s(2), s(3)...s(n)为主串，序列T=t(1), t(2), t(3)...t(m)为模式串，i和j分别为序列S和T的下标。当比较失败时，s(i) != t(j)，查找next数组得到next[j]。但是这个next[j]并不一定正确（假定，next[1]~next[j-1]都已经正确）：

1. 若新一轮开始比较的字符和上一轮中比较失败的字符不相等，即t( j ) != t( next[j] )，此时为真正的结束状态，不需要对next[j]做改动。
2. 若新一轮开始比较的字符和上一轮中比较失败的字符相等，即t( j ) == t( next[j] ) != s(i)， 此时要继续寻找next[j]的结束状态作为真正的结束状态。于是，有next[ j ] = next[ next[ j ] ]，修正完成。

按照序列的描述，对上一个例子中的模式串aaaab的next数组做修正：

•     j                 1  2  3  4  5
• 模式串           a  a  a  a  b
• next[j]            0  1  2  3  4
• nextNew[j]     0  0  0  0  4

另外，对最开始的例子中的模式串abaabcac的next数组也做一次修正：

•    j                 1  2  3  4  5  6  7  8
• 模式串          a  b  a  a  b  c  a  c
• next[j]           0  1  1  2  2  3  1  2
• nextNew[j]    0  1  0  2  1  3  0  2

算法描述

实现（3）

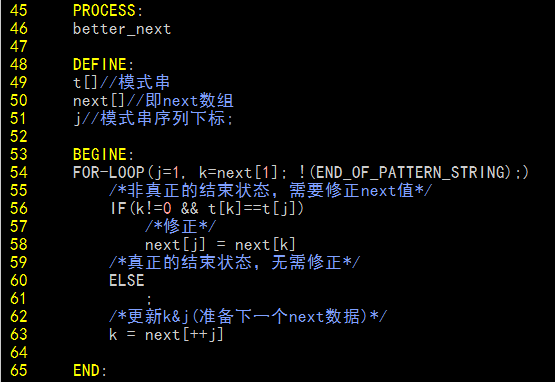
next数组“优化函数”（C实现）

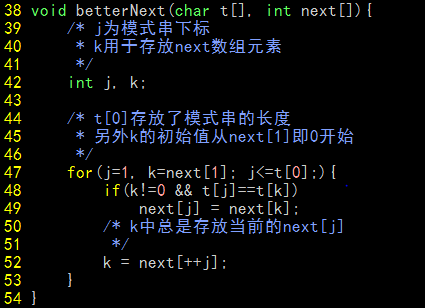
betterNext函数需要两个参数：模式串和未经修正的next数组，代码如下：

现在，通过调用getNext函数来得到“传统”的next数组，再将模式串和得到的数组放入betterNext中进行优化，便能得到理想的数据。

合并betterNext与getNext——getNextX（C实现）

在合并betterNext函数和getNext函数之前，再把迄今为止为止关于next数组的思路整理一遍。然后，用C实现全文的最终版next函数——getNextX。

把熟悉的字符序列请上场。假设，字符序列S=s(1), s(2), s(3)...s(n)为主串，序列T=t(1), t(2), t(3)...t(m)为模式串，i和j分别为序列S和T的下标。当一轮匹配开始一段时间后，出现了比较失败，不妨设此时的情况为s(i+1) != t(j+1)，并且k = next[j]。首先是生成传统next数组的两点：

• 若t[j] == t[k]，意味着赋值，next[j+1] = k +1
• 若t[j] != t[k]，意味着循环做k = next[k]直到t[j] == t[k]（暂不考虑0情况），接着赋值，next[j+1] = k +1

然后是修正部分的两点：

• 若t[j+1] != t[k+1]，意味着不用做任何事情
• 若t[j+1] == t[k+1]，意味着赋值，next[j+1] = next[k+1]

观察上诉四点，整理四个关系，然后顺利地写出下面这段最终版本的代码：



总结

至此，关于KMP算法的内容就讲诉完了。最后，像过电影一样在大脑里再回放一遍：

我们先了解了什么叫做字符串匹配算法（游标的滑动规则），并引入了最直观的plain match算法。通过分析plain match中存在的“主串游标回溯过远问题”，我们提出了改进方案，即KMP算法的第一个描述，同时附带避免了主串游标的回溯。接着，我们针对所谓的“恰当（理想）位置”，对比较失败后的模式串滑动做了更加细致的分析，并由此引入了状态集合P和Q以及它们的交集Z，同时给出了KMP算法的第二个描述以及一条很棒的用于选取“结束状态”的原则。后续中，我们一直遵循着这条原则进行分析和操作。在此基础上，通过对序列作分析，提出了KMP算法的基石，并由此引出了next数组。next数组可以按照我们设定的三条规则手工生成，也可以机械地运用算法来让代码实现。算法的推导运用了数学归纳法以及KMP算法本身的思想，有许多值得思考的地方。但是，在一些特殊的模式串中，这种算法产生的next数组还不够完美。于是，在拓展中，重新回顾了“结束状态的原则”，并对一类模式串的next数组做了修正。由此，思路变得更加开阔，对不同的模式串，应当思考恰当的next数组生成算法。这就可以认为是KMP算法的无限生命力所在吧。

参考资料

严蔚敏老师的《数据结构》是本文主要的参考资料，同时，也是自己数据结构的课程教材。对于这本书，我认为内容很全，其中的推导部分，也都写得比较完整&严谨。形式上枯燥并不影响一本书的含金量，关键是你从中汲取的价值，至少我是这样认为的，也因此向所有学习数据结构的同学推荐这本书。

最后，向KMP算法的创作者D.E.Knuth，V.R.Pratt，J.H.Morris致敬！