理解复数

复数的奇怪之处在于虚数单位i,直接定义i·i=-1让人无法接受。
主要来讨论复数的乘法。复数的乘法拓宽了实数乘法的表示范围。实数的乘法a·b仅表示a的长度伸缩b的长度倍。复数的乘法a·b不仅将a的长度伸缩b的长度倍，还将a逆时针旋转了b的角度。来看下虚数单位i:

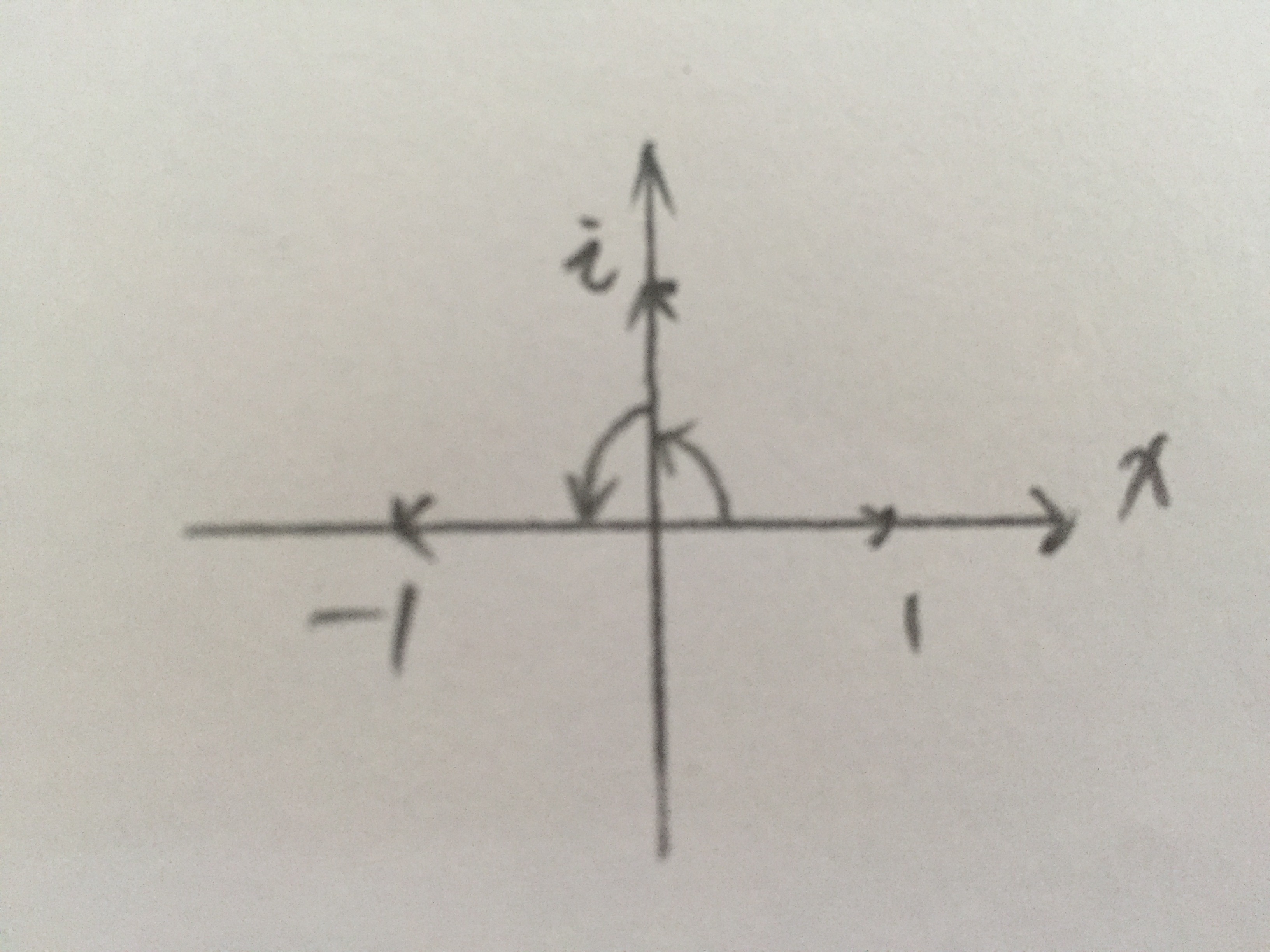
图(1)
1表示长度为1，角度是0的向量
i表示长度为1，角度是90度的向量
1·i表示将1逆时针旋转90度，长度不变，得到的结果就是i
i·i表示将i逆时针旋转90度，长度不变，得到的结果是-1
这就是i·i=-1的由来。
一个复数a+bi表示从起始点出发沿X轴移动a个单位，然后逆时针旋转90度再移动b个单位。这就拓宽了数的表示范围，实数只能表示X轴上的点，复数可以表示整个平面上的点。
当然，复数乘法不是随便定义的，它必须尽可能地满足乘法运算法则。

回顾一下乘法运算法则：
乘法分配律
两个数的和同一个数相乘,等于把两个加数分别同这个数相乘,再把两个积加起来,和不变。
(a+b)×c =a×c+b×c

乘法交换律
乘法交换律是两个数相乘,交换因数的位置,它们的积不变。
a×b=b×a

我们来看看复数乘法是否满足这些法则

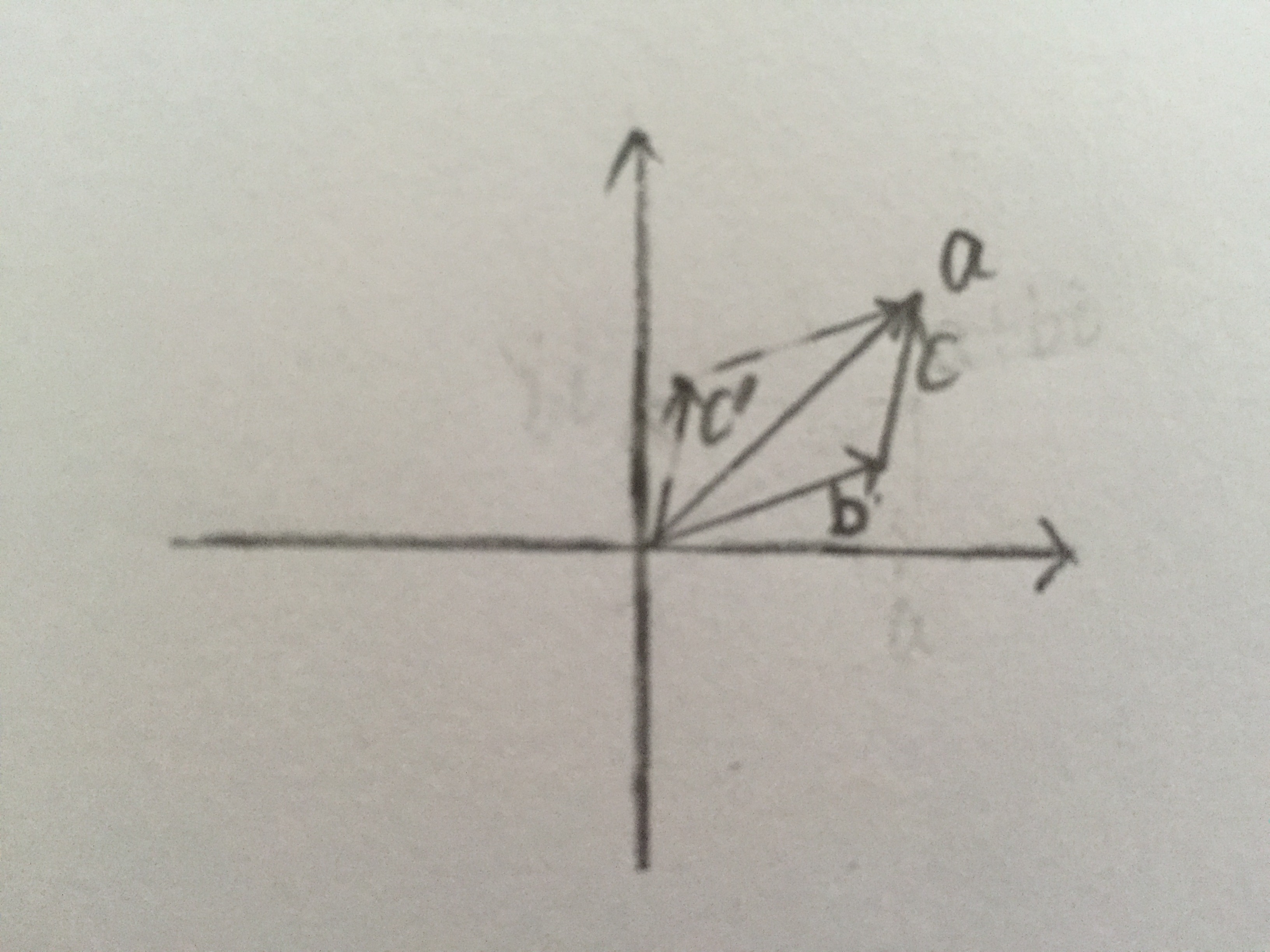
图(2)
上图复数a分解成了复数b+c，a=b+c
c’是将c的起始点挪到了原点，其实它还是c
大家可能看出来了，复数和向量有很大的相似性，加法的定义基本上是一样的。事实上我都是把复数当向量用的，严格来讲区别肯定是有的。至于区别在哪嘛，管他呢
来看图(2),a的分量b和c’围成了一个平行四边形，对于复数乘法a·d,按之前我们的理解，等于将复数a放大d的长度倍，然后再旋转d的角度。
再来看看b·d和c·d(也就是c’·d),将b和c’放大d的长度倍，想象一下将图(2)的整个平行四边形整体放大d的长度倍，他们的和与直接将a放大d的长度倍是一样的，大小也没有发生改变。
(a·d)的长度 = (b·d)的长度+(c’·d)的长度 = (b·d)的长度+(c·d)的长度
接着将放大后的整个平行四边形绕原点逆时针旋转d的角度，平行四边形的形状不会发生改变，旋转后的b+旋转后的c’ = 旋转后的a 仍然成立
a·d = b·d+c·d成立，复数乘法满足分配律。

交换律的证明比较简单，a·b和b·a的大小都是a的长度·b的长度，角度都是a的角度+b的角度
还有一点，两个复数的乘积还是一个复数
相对于向量的点积和叉积，点积的乘积丢失了方向，叉积并不完全满足交换律(差了一个负号)，复数乘法完美满足分配律和交换律。