图的周游，最短路径和最小生成树

• 图的周游

给出一个图G和其中任意一个顶点V0，从V0出发系统地访问G中所有的顶点，每个顶点访问一次。

1. 深度优先

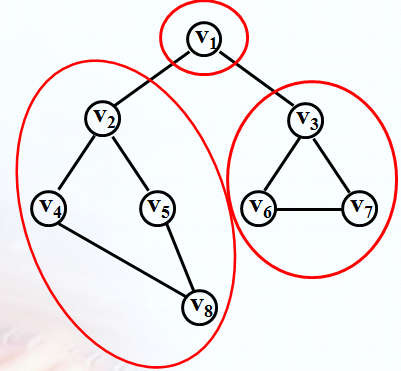
访问一个顶点V，然后访问该顶点邻接到的未被访问过的顶点V’，再从V’出发递归地按照深度优先的方式周游，当遇到一个所有邻接于它的顶点都被访问过了的顶点U时，则回到已访问顶点序列中最后一个拥有未被访问的相邻顶点的顶点W，再从W出发递归地按照深度优先的方式周游，最后，当任何已被访问过的顶点都没有未被访问的相邻顶点时，则周游结束。

划分为基结点，第一个邻接结点导出的子图，其它邻接顶点导出的子图。

深度优先搜索是类似于树的一种先序遍历：V1，V2，V4，V8，V5，V3，V6，V7.

深度优先搜索算法的时间复杂度：总代价为Θ(|V|+|V|2)= Θ(|V|2)。

2. 广度优先

它的基本思想是访问顶点V0，然后访问V0邻接到的所有未被访问过的顶点V01，V02，…V0i，再依次访问V01，V02，…V0i邻接到的所有未被访问的顶点，如此进行下去，直到访问遍所有的顶点。

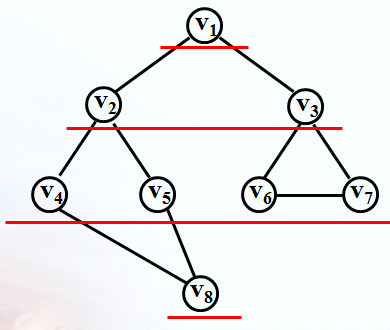
把图人为的分层，按层遍历。

广度优先搜索类似于树的层次遍历，广度优先搜索次序为：V1，V2，V3，V4，V5，V6，V7,,V8.

• 最短路径

1. 单源最短路径（DIjkstra算法）

寻找从单个源点到其余各顶点的最短路径算法：

思想：贪心算法(局部最优)，按路径长度递增的次序产生最短路径。利用已得到的顶点的最短路径来计算其它顶点的最短路径。权值是一个非负实数。

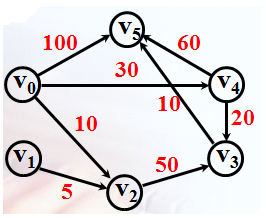
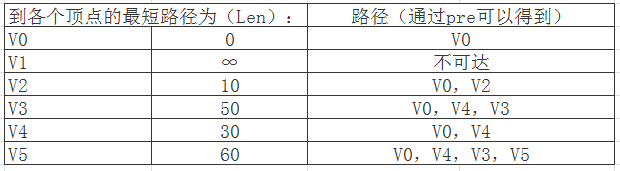
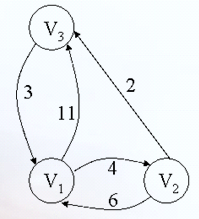
例如：求从 v0到其余各顶点的最短路径。D[i] 表示 v0 到 vi 的最短路径的长度，Path[i]表示v0 到 vi 的最短路径。

1.  初始，D[i]的值为 v0 到 vi 的弧的权值。显然，D[i] 中的最小值 D[2] 便是 v0到 v2 的最短路径的长度，Path[2]=( v0  , v2 )。

 

2. 设下一条最短路径的终点是 vj ，则这条最短路径或者是 ( v0 , vj ) 、或者是  v0  经过 v2 到达 vj 的路径 ；其中取 D[i](D[2]除外) 中的最小值得到 v4，Path[4]=( v0  , v4 ) 。

 

3. 设下一条最短路径的终点是 vk ，则这条最短路径或者是 ( v0 , vk ) 、或者是  v0  经过 v2 或 v4 到达 vk 的路径 ；取 D[i](D[2]、D[4] 除外) 中的最小值得到 v3 ，Path[3]=( v0  , v4 , v3 ) 。

 

 

除了上面那种方式外，还有另外一种方法（不过思想都是一样的）：

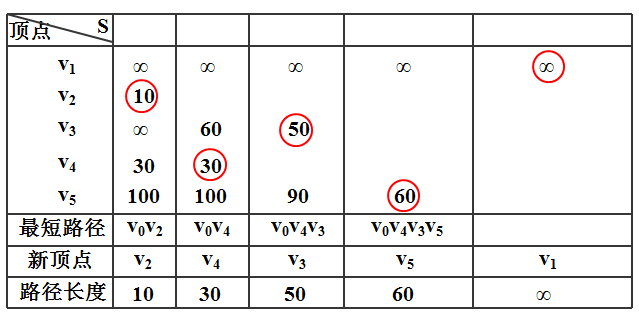
定义一个顶点集合S，和两个长度为顶点数的数组，一个（len）存储借助当前S集合中的顶点顶点i到其他所有节点的最短路径的长度len[i]，一个存储最短路径中在该顶点i前一个顶点值pre[i]。

 初始时S中只有顶点V0，所有的pre[i]都置为0，即初始时，V0到所有顶点的最短路径中，所有顶点的前一个顶点都是V0，然后借助S集合中的顶点，求到其他所有顶点的最短路径len[i],然后找出len[i]中最小的一个len[j]，接着将Vj加入S集合，然后再算len[i]，这时只要比较V0通过Vj到达Vi的距离和V0直接到达Vi的距离谁小，如果V0通过Vj到达Vi的距离小，则将pre[i] =j，len[i]=[V0->Vj->Vi的距离]；说明通过Vj顶点，可以缩短V0到Vi的距离，反之则不改变len[i]和pre[i]的值。就这样一直递归，直到所有的节点都加入S集合。

下面是用表格表示的该过程：

求得结果：

DIjKstra算法的复杂度为O（n2）。

 

2. 每对顶点之间的最短路径（Floyd算法）

算法思想：

假设用相邻矩阵adj表示图，Floyd算法递归地产生一个矩阵序列adj(0)，adj(1)，…， adj(k) ，…， adj(n)。

adj(k)[i，j]等于从顶点Vi到顶点Vj中间顶点序号不大于k的最短路径长度。

最关键的部分：

假设已求得矩阵adj(k-1)，那么从顶点Vi到顶点Vj中间顶点的序号不大于k的最短路径有两种情况：

一种是中间不经过顶点Vk，那么就有

    adj(k)[i，j]=adj(k-1)[i，j]

另一种是中间经过顶点Vk，那么

adj(k)[i，j]< adj(k-1)[i，j]，且adj(k)[i，j]=adj(k-1)[i，k]+ adj(k-1)[k，j]

Path矩阵的作用：Path[i，j]表示从顶点i到顶点j的最短路径中排在顶点j前面的那个顶点。

例如：

 

Floyd算法和将DIjstra算法运算n次非常相似。每个adj(i)矩阵可以看做是有一个顶点集合S，而这个S所包含的顶点为{V0，V1，...，Vi-1}，而每个Path[I,j],就相当于pre。对于稠密图，效率要高于执行|V|次Dijkstra算法。

 

• 最小生成树

假设要在N个城市之间建立通信网路哦，要在最节省经费的情况下建立这个通信网络，则连通N个城市需要N-1条通信线路。那么，如何在这些可能的线路中选择N-1条线路，使得线路开销最小？最小生成树就可以解决这类问题。

生成树：

如果一个连通图 G的一个包含所有顶点的极小连通子图 T 有如下特点：

（1） T 包含 G 的所有顶点 n 个

（2） T 为连通子图

（3） T 包含的边数最少（n-1个）

那么(T 是一棵有 n个顶点，n-1 条边的生成树（支撑树）。

性质: 一个有n个顶点的连通图的生成树有且仅有n-1条边。一个连通图的生成树可能并不唯一。

最小生成树：

生成树的代价:为树上各边的权之总和。代价最小的生成树称为最小生成树。

求最小生成树：

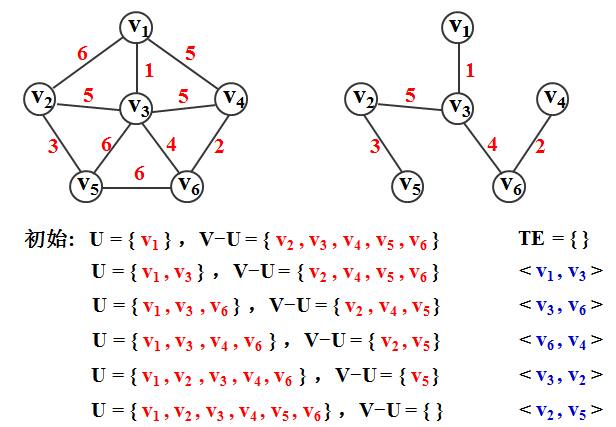
1. 普里姆算法（Prim）

思想：

如果N = ( V , E )是具有 n 个顶点的连通图，设 U 是最小生成树中顶点的集合，设 TE 是最小生成树中边的集合；

初始，U= { u1 } ，TE = { } ，

重复执行:

在所有u∈U，v∈V-U 的边 ( u , v ) 中寻找代价最小的边( u’ , v’ ) ，并纳入集合 TE 中；

同时将v’ 纳入集合 U 中；

直至U = V 为止。

集合TE 中必有 n-1 条边。

图示：

 

2. 克鲁斯卡尔(Kruskal)算法

思想：

设有一个有 n 个顶点的连通网络 N = { V, E },最初先构造一个只有n 个顶点，没有边的非连通图 T = { V, Φ},   图中每个顶点自成一个连通分量。当在 E 中选到一条具有最小权值的边时,若该边的两个顶点落在不同的连通分量上（说明图中无环），则将此边加入到 T 中；否则将此边舍去，重新选择一条权值最小的边。如此重复下去，直到所有顶点在同一个连通分量上为止。

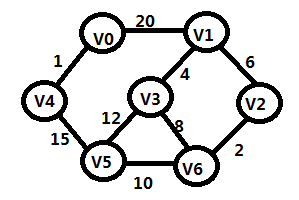
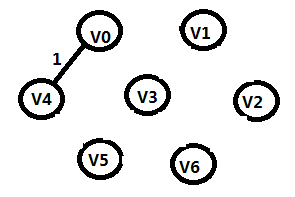
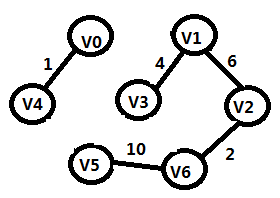
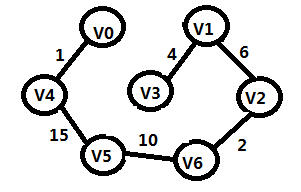
例求如下图的最小生成树：

TE={}

步骤1：

TE={（V0，V4）}

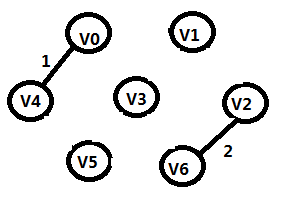
步骤2：

TE={（V0，V4），（V2，V6）}

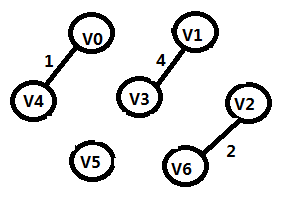
步骤3：

TE={（V0，V4），（V2，V6），（V1，V4）}

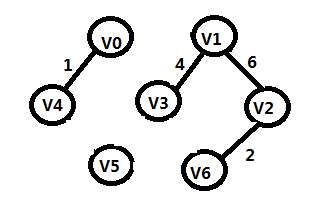
步骤4：

TE={（V0，V4），（V2，V6），（V1，V4），（V1，V2）}

步骤5：

TE={（V0，V4），（V2，V6），（V1，V4），（V1，V2），（V5，V6）}

步骤6：

 

TE={（V0，V4），（V2，V6），（V1，V4），（V1，V2），（V5，V6），（V4，V5）}

3. 两种算法的比较

Prim算法

算法时间复杂度:O(n2)

与边的个数无关；

适合于求边稠密的网的最小生成树。

Kruskal算法

算法时间复杂度:O(eloge)   (e为网的边的数目)    

适合于求边稀疏的网的最小生成树。