经典排序算法-快速排序（挖坑法、前后指针法）、基数排序

快速排序在实际应用中是比较表现好的排序算法。快速排序我用两种方法实现它。

第一种为方法，形象的称为：挖坑法

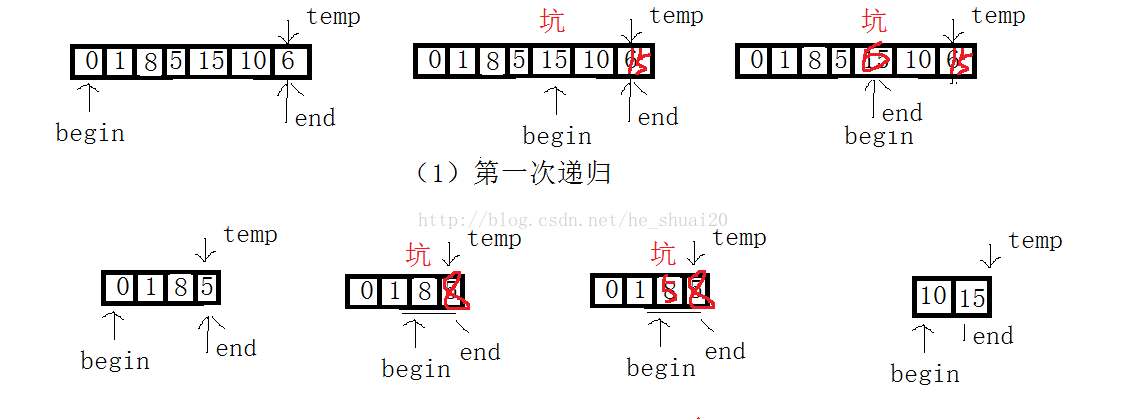
基本思路：1、寻找pos位，然后将其分为两段数组，然后对这两段数组递归排序；

                    2、指定一个基数temp（三数取中法），定义两个指针begin一个指向起始位置，end一个指向最后一个元素的位置。begin寻找比基数（temp）大的数字，找到 后将begin的数据赋给end，begin成为一个坑，然后end寻找比基数（temp）小的数字，找到将end的数据赋给begin，end成为一个新坑，循环这个过程，直到begin指针与end指针相遇，然后将temp的数据返回给那个坑，然后进行递归操作。

 代码实现为：

int PastSort1(int *arr, int left, int right)  //挖坑法
{
	int begin = left;
	int end = right;
	int temp = arr[mid(arr,left,right)];
	while (begin < end)
	{
		while (begin < end && arr[begin] <= temp)
			begin++;
		if (begin < end)
			arr[end] = arr[begin];//begin成为新坑
		while (begin < end && arr[end] >= temp)
			end--;
		if (begin < end)
			arr[begin] = arr[end];  //end成为新坑
	}

	arr[begin] = temp;  //将temp填补进去
	return begin;
}


void QuickSort(int *arr,int left,int right)
{
	if (arr == NULL || left > right)
		return;

	int pos = PastSort1(arr, left, right);

	QuickSort(arr, left, pos - 1);
	QuickSort(arr, pos + 1, right);
}

前后指针法：

定义两个指针，一前一后，前面指针找比基数小的数，后面指针找比基数大的数，前面的指针找到后，将前后指针所指向的数据交换，当前面的指针遍历完整个数组时，将基数值与后指针的后一个位置的数据进行交换，然后以后指针的后一个位置作为分界，然后将数组分开，进行递归排序。

代码实现：

int PastSort2(int* arr, int left, int right)  //前后指针法
{
	int cur = left;  //找小
	int ptr = left-1;//找大
	int temp = arr[mid(arr, left, right)];
	while (cur < right)
	{
		if (arr[cur] < temp)
		{
			swap(arr[cur], arr[++ptr]);
		}
		cur++;
	}
	swap(arr[++ptr], arr[right]);
	return ptr;
}

void QuickSort(int *arr,int left,int right)
{
	if (arr == NULL || left > right)
		return;

	int pos = PastSort2(arr, left, right);

	QuickSort(arr, left, pos - 1);
	QuickSort(arr, pos + 1, right);
}

基数排序：

基本原理是：

代码实现为：

int getbit(int* arr,int size)  //获得最大位数
{
	int bits = 1;
	int rang = 10;
	for (int i = 0; i < size; ++i)
	{
		while (arr[i] >= rang)
		{		
			++bits;
			rang *= 10;
		}
	}
	return bits;
}

void BucketSort(int* arr, int size)
{
	int bits = getbit(arr, size);
	int radix = 1;
	int count[10];
	for (int bit = 1; bit <= bits;bit++)  //循环最大位数次
	{
		memset(count, 0, sizeof(int)* 10);
		for (int i = 0; i < size; ++i)//统计数字位数的数量
		{
			int index = (arr[i] / radix) % 10;
			count[index]++;
		}

		for (int j = 1; j < 10; j++)  //固定数值排序的位置
		{
			count[j] = count[j] + count[j - 1];
		}
		int *str = new int[size];
		memset(str, 0, sizeof(int)*size);
		for (int i = size-1; i >=0; i--)//按照固定的位置将数据写入辅助数组
		{
			int index = (arr[i] / radix) % 10;
			str[count[index]-1] = arr[i];
			count[index]--;
		}
		radix = radix * 10;
		for (int i = 0; i < size; i++) //将辅助数组中的数拷贝回原数组
		{
			arr[i] = str[i];
		}
		delete[] str;
	}
}

前面我用了三篇文章来写几种常见的排序方法，我用一个图简单分析一下他们的最好最坏平均时间复杂度，以及空间复杂度，与稳定性分析。