关于图的现实应用:
软件开发:编译器会使用图来表示大型软件系统中各个模块之间的关系。图中的结点即构成整个系统的各个类和模块,连接则为类的方法之间的可能调用关系(静态分析),或是系统运行时实际调用关系(动态分析)。
我们将学习四种图:
1.无向图(简单连接)
2.有向图(连接有方向)
3.加权图(连接带有权值)
4.加权有向图(连接既有方向性又带有权值)
4.1无向图
特殊的图(两种特殊情况):
1.自环,即一条连接一个顶点和其自身的边
2.连接同一对顶点的两条边称为平行边
将含有平行边的图称为多重图,将没有平行边或自环的图称为简单图。
某个顶点的度数即为依附于它的边的总数。
路径或者环的长度为其中所包含的边数。
定义:如果从任意一个顶点都存在一条路径到达另一个任意顶点,我们称这幅图为连通图。
图与树之间的关系:
当且仅当一幅含有V个结点的图G满足下列5个条件之一时,他就是一棵树:
1.G有V-1条边且不含有环
2.G有V-1条边且是连通的
3.G是连通的,但删除任意一条边都会使他不再连通
4.G是无环图,但增加任意一条边都会产生一条环
5.G中的任意一对顶点之间仅存在一条简单路径
图的密度:已经连接的顶点对占所有可能被连接的顶点对的比例。
二分图:一种能够将所有结点分成两部分的图,其中图的每条边所连接的两个顶点都分别属于不同的部分。
无向图的API:
//创建一个含有v个顶点但不含边的图
Graph(int v);
//顶点数
int V();
//边数
int E();
//向图中添加一条边v-w
void addEdge(int v,int w);
//和v相邻的所有顶点
Iterable<Integer> adj(int v);我们研究算法或一个数据结构时,总是先想其所应该提供的API,由低级的API构成高级的API,低级API直接和具体的实现方式关联。注意计算机领域抽象的思想。
图的几种表示方法:
用哪种方式(数据结构)来实现图并实现其API。要求:
1.它必须为可能在应用中碰到的各种类型的图预留出足够的空间
2.Graph的实例方法的实现必须要快–他们是开发处理图的各种用例的基础
几种备选:
1.邻接矩阵,用V*V的布尔矩阵表示。不满足第一条件–V*V个布尔值所需空间太大
2.边的数组,可以使用一个Edge类,它含有两个int实例变量。表示方法简洁但是不满足第二条件–要实现adj()需要检查图中的所有边(这种表示方法是站在边的角度上)
3.邻接表数组。我们使用一个以顶点为索引的列表数组,其中的每个元素都是和该顶点相邻的顶点列表。
这种Graph的实现的性能有如下性能:
1.使用的空间和V+E成正比。
2.添加一条边所需的时间为常数
3.遍历顶点V的所有相邻顶点所需时间和V的度数成正比(处理每个相邻顶点所需的时间为常数)
Graph数据类型:
public class Graph{
private final int V;//顶点数目
private int E;//边的数目
private Bag<Integer>[] adj;//邻接表
public Graph(int V){
this.V = V;
this.E = 0;
adj = (Bag<Integer>[]) new Bag[V];//创建邻接表
for(int v = 0;v<V;v++){
adj[v] = new Bag<Integer>();
}
}
public int V(){return V;}
public int E(){return E;}
public void addEdge(int v,int w){
adj[v].add(w);
adj[w].add(v);
E++;
}
public Iterable<Integer> adj(int v){ return adj[v];}
}
public class Bag<Item> implements Iterable<Item> {
//链表实现Bag
private Node first;//链表首结点
private class Node{
Item item;
Node next;
}
//和stack的push方法完全相同,在头部添加
public void add(Item item){
Node oldFirst = first;
first = new Node();
first.item = item;
first.next = oldFirst;
}
@Override
public Iterator<Item> iterator() {
return new ListIterator();
}
private class ListIterator implements Iterator<Item>{
private Node current = first;
@Override
public boolean hasNext() {
return current!=null;
}
@Override
public Item next() {
Item item = current.item;
current = current.next;
return item;
}
}
}
实际应用中可能还需要:
1.添加一个顶点
2.删除一个顶点
3.删除一条边
4.检查图中是否含有边v-w。
要实现这些方法(不允许存在平行边),我们可能需要用SET代替Bag来实现邻接表。我们称这种方法为邻接集。
深度优先搜索:
class DepthFirstSearch{
private boolean[] marked;
private int count;
public DepthFirstSearch(Graph G,int s){//找到和起点s连通的所有顶点
marked = new boolean[G.V()];
dfs(G,s);
}
private void dfs(Graph G,int w){
marked[w] = true;
count++;
for (int v:G.adj(w)) {
if(!marked[v]) dfs(G,v);
}
}
public boolean marked(int v){//v和s是连通的吗?
return marked[v];
}
public int count(){//与s连通的顶点总数
return count;
}
}
//上述算法在构造函数中处理一切运算,所以用例调用提供的对外方法能够返回最终结果算法思想:
要搜索一幅图,只需用一个递归方法来遍历所有顶点。在访问其中一个顶点时:
1.将它标记为已访问
2.递归地访问它的所有没有被标记过的邻居顶点
命题A:深度优先搜索标记与顶点连通的所有顶点所需的时间与顶点的度数之和成正比。
算法遍历边和访问顶点的顺序与图的表示有关,而不只是与图的结构或是算法有关。深度优先搜索中每条边都会被访问两次,这意味着深度优先搜索的轨迹可能比想象长一倍。图中仅含有8条边,但需要追踪算法在邻接表的16个元素上的操作。
寻找路径:
API:
class Paths{
Paths(Graph G,int s);//在G中找出所有起点为s的路径
boolean hasPathTo(int v);//是否存在从s到v的路径
Iterable<Integer> pathTo(int v);//s到v的路径,如果不存在返回null
}使用深度优先搜索图中的路径:
class DepthFirstPaths{
private boolean[] marked;
private int[] edgeTo;//该数组记录与索引该点相连的上一个顶点
private int s;
public DepthFirstPaths(Graph G,int s){
marked = new boolean[G.V()];
edgeTo = new int[G.V()];
this.s = s;
dfs(G,s);
}
private void dfs(Graph G,int w){
marked[w] = true;
for (int v:G.adj(w)) {
if(!marked[v]){
edgeTo[v] = w;//使用数组记录,v索引上记录上一点w
dfs(G,v);
}
}
}
public boolean hasPathTo(int v){
return marked[v];
}
public Iterable<Integer> pathTo(int v){
if(!hasPathTo(v)) return null;
Stack<Integer> path = new Stack<>();
for (int i = v; i !=s; i = edgeTo[i]) {//不断回溯
path.push(i);
}
path.push(s);
return path;
}
}算法思想:pathTo方法用变量i遍历整棵树,将i设为edgeTo[i],然后在到达s之前,将遇到的所有顶点都压入栈中。将这个栈返回一个Iterable对象帮助用例遍历s到v的路径。
这个路径就是一条路径,可能从s到v有多条路径,但这种方法只会返回一条。这条路径是根据数据结构的顺序和DFS算法决定的。
广度优先搜索:
在广度优先搜索中,我们希望按照与起点的距离的顺序来遍历所有顶点。实现:使用(FIFO,先进先出)队列来代替栈(LIFO,后进先出)。因为深度优先是递归调用,所以其内部的执行顺序为栈。
算法思想:
先将起点加入队列,然后重复以下步骤直到队列为空:
1.取队列中的下一个顶点v并标记它
2.将与v相邻的所有未被标记过的顶点加入队列
class Queue<Item> implements Iterable<Item>{
private Node first;
private Node last;
private int N;
private class Node{
Item item;
Node next;
}
public boolean isEmpty(){
return N==0;
}
public int size(){
return N;
}
public void enqueue(Item item){
//向表尾添加数据
Node oldLast = last;
last = new Node();
last.item = item;
last.next = null;
if(isEmpty()) first = last;//首尾是同一个
else oldLast.next = last;
N++;
}
public Item dequeue(){
//从表头删除元素
Item item = first.item;
first = first.next;
if(isEmpty()) last = null;
else
N--;
return item;
}
@Override
public Iterator<Item> iterator() {
// TODO Auto-generated method stub
return new ListIterator();
}
private class ListIterator implements Iterator<Item>{
private Node current = first;
@Override
public boolean hasNext() {
return current!=null;
}
@Override
public Item next() {
Item item = current.item;
current = current.next;
return item;
}
}
}
class BreadthFirstPaths{
private boolean[] marked;
private int[] edgeTo;//该数组记录与索引该点相连的上一个顶点
private int s;
public BreadthFirstPaths(Graph G,int s){
marked = new boolean[G.V()];
edgeTo = new int[G.V()];
this.s = s;
bfs(G,s);
}
private void bfs(Graph G,int s){
Queue<Integer> queue = new Queue<>();
marked[s] = true;
queue.enqueue(s);//将顶点加入队列
while(!queue.isEmpty()){
int v = queue.dequeue();//从队列中删除下一个顶点
for(int w:G.adj(v)){
if(!marked[w]){//对于每个未被标记的顶点
edgeTo[w] = v;
marked[w] = true;
queue.enqueue(w);//加入队列
}
}
}
}
public boolean hasPathTo(int v){
return marked[v];
}
public Iterable<Integer> pathTo(int v){
if(!hasPathTo(v)) return null;
Stack<Integer> path = new Stack<>();
for (int i = v; i !=s; i = edgeTo[i]) {//不断回溯
path.push(i);
}
path.push(s);
return path;
}
}使用广度优先搜索,以找出图中从构造函数得到的起点s到其他所有顶点的最短路径。bfs方法会标记所有与s连通的顶点,因此用例可以调用hasPathTo来判定一个顶点与s是否连通并使用pathTo得到一条从s到v的路径,确保没有其他从s到v的路径所含的边比这条路径更少。
命题B:对于s可达的任意顶点v,广度优先搜索都能找到一条从s到v的最短路径。
深度和广度的特点:
相同:
在搜索中都会先将起点存入数据结构,然后重复以下步骤直到数据结构被清空:
1.取其中的下一个顶点并标记它
2.将v的所有相邻而未被标记的顶点加入数据结构
不同:
从数据结构中获取下一个顶点的规则(广度为最早加入的顶点,深度为最晚加入的顶点)
连通分量:
连通分量的API:
class CC{
CC(Graph G);//预处理构造函数
boolean connected(int v,int w);//v和w连通吗
int count();//连通分量数
int id(int v);//v所在的连通分量的标识(0到count-1)
}实现:
class CC{
private boolean[] marked;
private int [] id;
private int count;
public CC(Graph G){
marked = new boolean[G.V()];
id = new int[G.V()];
for (int s = 0; s < G.V(); s++) {
if(!marked[s]){
dfs(G,s);
count++;
}
}
}
private void dfs(Graph G,int w){
marked[w] = true;
id[w] = count;
for (int v:G.adj(w)) {
if(!marked[v]){
dfs(G,v);
}
}
}
public boolean connected(int v,int w){
return id[v]==id[w];
}
public int id(int v){
return id[v];
}
public int count(){
return count;
}
}命题C:深度优先搜索的预处理使用的时间和空间与V+E成正比且可以在常数时间内处理关于图的连通性查询。
union-find算法:
union-find算法是一种动态算法(我们在任何时候都能用接近常数的时间检查两个顶点是否连通,甚至是在添加一条边的时候),但深度优先搜索则必须要对图进行预处理。因此,我们在完成只需要判断连通性或是需要完成有大量连通性查询和插入操作混合等类似的任务时,更倾向使用union-find算法,而深度优先搜索更适合实现图的抽象数据类型,因为它能更有效地利用已有的数据结构。
怎样检验无向图G**是否为无环图**?
stackoverflow上的答案:
1.
The graph has a cycle if and only if there exists a back edge. A back edge is an edge that is from a node to itself (selfloop) or one of its ancestor in the tree produced by DFS forming a cycle.
Both approaches above actually mean the same. However, this method can be applied only to undirected graphs.
The reason why this algorithm doesn’t work for directed graphs is that in a directed graph 2 different paths to the same vertex don’t make a cycle. For example: A–>B, B–>C, A–>C - don’t make a cycle whereas in undirected ones: A–B, B–C, C–A does.
Find a cycle in undirected graphs
An undirected graph has a cycle if and only if a depth-first search (DFS) finds an edge that points to an already-visited vertex (a back edge).
Find a cycle in directed graphs
In addition to visited vertices we need to keep track of vertices currently in recursion stack of function for DFS traversal. If we reach a vertex that is already in the recursion stack, then there is a cycle in the tree.
2.
For every visited vertex ‘v’, if there is an adjacent ‘u’ such that u is already visited and u is not parent of v, then there is a cycle in graph. If we don’t find such an adjacent for any vertex, we say that there is no cycle. The assumption of this approach is that there are no parallel edges between any two vertices.
算法实现:
class Cycle{
private boolean[] marked;
private boolean hasCycle;
public Cycle(Graph G){
marked = new boolean[G.V()];
for (int i = 0; i < G.V(); i++) {
if(!marked[i]){
dfs(G,i,i);//记录当前结点的父结点
}
}
}
//如果当前结点的下一个已经visited的结点不是自己的父结点,那么就存在环
private void dfs(Graph G,int v,int parent){
marked[v] = true;
for(int w:G.adj(v)){
if(!marked[w]){
dfs(G,w,v);
}else if(w!=parent){
hasCycle = true;
}
}
}
public boolean hasCycle(){
return hasCycle;
}
}判断无向图G是否为二分图(双色问题):
class TwoColor{
private boolean[] marked;
private boolean[] color;
private boolean isTwoColor=true;
public TwoColor(Graph G){
marked = new boolean[G.V()];
color = new boolean[G.V()];
for (int i = 0; i < G.V(); i++) {
if(!marked[i]){
dfs(G,i);
}
}
}
private void dfs(Graph G,int v){
marked[v] = true;
for(int w:G.adj(v)){
if(!marked[w]){
color[w] = !color[v];
dfs(G,w);
}else if(color[w]== color[v]){
isTwoColor = false;
}
}
}
public boolean isTwoColor(){
return isTwoColor;
}
}4.2有向图
定义:由一组顶点和一组有方向的边组成,每条有方向的边都连接着有序的一对顶点。一个顶点的出度为由该顶点指出的边的总数,一个顶点的入度为指向该顶点的边的总数。
有向图还是使用邻接表表示,比无向图还简单。
Digraph数据类型与Graph类型基本相同,只是addEdge只调用了一个add,它还有一个reverse方法来返回图的反向图:
public Digraph reverse(){
Digraph R = new Digraph(V);
for (int v = 0; v < V; v++) {
for(int w:adj(v)){
R.addEdge(w,v);
}
}
return R;
}单点可达性:给定一幅图和一个起点s,是否存在一条从s到达给定顶点v的有向路径。
多点可达性:给定一幅图和顶点的集合,是否存在一条从集合中的任意顶点到达给定顶点v的有向路径。
多点可达性的一个重要的实际应用:在典型的内存管理系统中,包括很多java的实现。
有向图的算法和数据结构跟无向图都差不多。
有向环:
调度问题,拓扑排序。
有向图中的环,如果一个有优先级限制的问题中存在有向环,那么这个问题肯定是无解的。
有向环的检测:
基于深度优先搜索:
一旦我们找到了一条有向边v–>w且w已经存在于栈中,那么就找到了一个环。因为栈表示的是一条由w到v的有向路径,而v–>w正好补全这个环。
//寻找有向环
class DirectedCycle{
private boolean[] marked;
private int[] edgeTo;
private boolean[] onStack;//递归调用的栈上的所有顶点
private Stack<Integer> cycle;//有向环中的所有顶点(如果存在)
public DirectedCycle(Graph G){
marked = new boolean[G.V()];
onStack = new boolean[G.V()];
edgeTo = new int[G.V()];
for (int i = 0; i < G.V(); i++) {
if(!marked[i]){
dfs(G,i);
}
}
}
private void dfs(Graph G,int v){
marked[v] = true;
onStack[v] = true;
if(this.hasCycle()){
return;
}
for(int w:G.adj(v)){
if(!marked[w]){
edgeTo[w] = v;
dfs(G,w);
}else if(onStack[w]){
cycle = new Stack<>();
for (int i = v; i !=w; i = edgeTo[i]) {
cycle.push(i);
}
cycle.push(w);
cycle.push(v);
}
}
onStack[v] = false;
}
public boolean hasCycle(){
return cycle!=null;
}
public Iterable<Integer> cycle(){
return cycle;
}
}命题F:当且仅当一幅图是无环图时它才能进行拓扑排序。
三种排列顺序:
1.前序:在递归调用之前将顶点加入队列
2.后序:在递归调用之后将顶点加入队列
3.逆后序:在递归调用之后将顶点压入栈
命题F:一副有向无环图的拓扑顺序即为所有顶点的逆后序排列。
有向环的检测是排序的前提。解决任务调度类应用通常需要三步:
1.指明任务和优先级条件
2.不断检测并去除有向图中的所有环,以确保存在可行方案
3.使用拓扑排序解决调度问题
有向图中的强连通性:
定义:如果两个顶点v和w是互相可达的,则称他们为强连通的。如果一副有向图中的任意两个顶点都是强连通的,则称这幅有向图也是强连通的。
两个顶点是强连通的当且仅当他们都在一个普通的有向环中。
作为一种等价关系,强连通性将所有顶点分成了一些等价类,每个等价类都是由相互均为强连通的顶点的最大子集组成的。
一个强连通图只含有一个强连通分量,而一个有向无环图中则含有V个强连通分量。
计算强连通分量的Kosaraju算法:
//基于深度优先搜索的顶点排序
public class DepthFirstOrder{
private boolean[] marked;
private Queue<Integer> pre;//前序排列
private Queue<Integer> post;//后序排列
private Stack<Integer> reversePost;//逆后序排列
public DepthFirstOrder(Digraph G){
pre = new Queue<Integer>();
post = new Queue<Integer>();
reversePost = new Stack<Integer>();
marked = new boolean[G.V()];
for (int i = 0; i < G.V(); i++) {
if(!marked[i]){
dfs(G,i);
}
}
}
private void dfs(Graph G,int v){
pre.enqueue(v);
marked[v] = true;
for(int w:G.adj(v)){
if(!marked[w]){
dfs(G,w);
}
}
post.enqueue(v);
reversePost.push(v);
}
public Iterable<Integer> pre(){
return pre;
}
public Iterable<Integer> post(){
return post;
}
public Iterable<Integer> reversePost(){
return reversePost;
}
}
class KosarajuSCC{
private boolean[] marked;//已经访问过的顶点
private int [] id;//强连通分量标识
private int count;//强连通分量的数量
public KosarajuSCC(Graph G){
marked = new boolean[G.V()];
id = new int[G.V()];
DepthFirstOrder order = new DepthFirstOrder(G.reverse());
for (int s:order.reversePost()) {
if(!marked[s]){
dfs(G,s);
count++;
}
}
}
private void dfs(Graph G,int w){
marked[w] = true;
id[w] = count;
for (int v:G.adj(w)) {
if(!marked[v]){
dfs(G,v);
}
}
}
public boolean stronglyConnected(int v,int w){
return id[v]==id[w];
}
public int id(int v){
return id[v];
}
public int count(){
return count;
}
}为了找到所有强连通分量,它会在反向图中进行深度优先搜索来将顶点排序(搜索顺序的逆后序),在给定有向图中用这个顺序再进行一次深度优先搜索。
命题H:使用深度优先搜索查找给定有向图G的反向图Gr,根据由此得到的所有顶点的逆后序再次用深度优先搜索处理有向图G(kosaraju算法),其构造函数中的每一次递归调用所标记的顶点都在同一个强连通分量之中。
再谈可达性:
顶点对的可达性:是否存在一条从一个给定的顶点v到另一个给定的顶点w的路径?
对于无向图,这个问题等价于连通性问题。对于有向图,它和强连通性的问题有很大区别。CC实现需要线性级别的预处理时间才能支持常数时间的查询操作。
定义:有向图G的传递闭包是由相同的一组顶点组成的另一幅有向图,在传递闭包中存在一条从v指向w的边当且仅当在G中w是从v可达的。
简单说,就是将自环,直接可达(原始图中的边),间接可达放入数组,方便常数级别的查询。
实现:
//有向图的可达性
//这份深度优先搜索的实现能够判断从给定的一个顶点或者一组顶点能到达哪些其他顶点
class DirectedDFS{
private boolean[] marked;
public DirectedDFS(Digraph G,int s){
marked = new boolean[G.V()];
dfs(G,s);
}
public DirectedDFS(Digraph G,Iterable<Integer> sources){
marked = new boolean[G.V()];
for(int s:sources){
if(!marked[s]){
dfs(G,s);
}
}
}
private void dfs(Digraph G,int v){
marked[v] = true;
for(int w:G.adj(v)){
if(!marked[w]) dfs(G,w);
}
}
public boolean marked(int v){
return marked[v];
}
}
class TransitiveClosure{
private DirectedDFS[] all;
TransitiveClosure(Digraph G){
all = new DirectedDFS[G.V()];
for (int i = 0; i < G.V(); i++) {
//对于每个顶点来说,能够到达哪些顶点
all[i] = new DirectedDFS(G,v);
}
}
boolean reachable(int v,int w){
return all[v].marked(w);
}
}本质上,TransitiveClosure通过计算G的传递闭包来支持常数时间的查询–传递闭包矩阵中的第v行就是TransitiveClosure类中的DirectedDFS[] 数组的第v个元素的marked[] 数组。
总结:








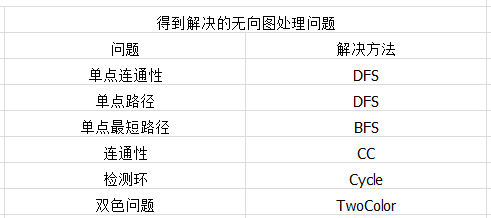
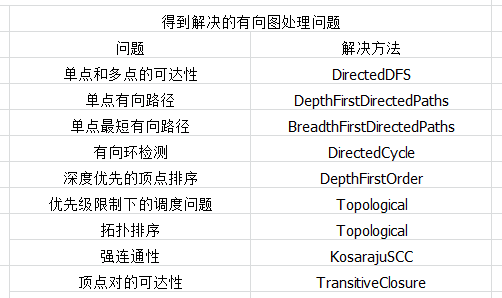













 683
683











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








