主动降噪开发之四——多通道算法实现

---

前言

噪声主动控制在实际应用的过程中其实存在很多的问题，比如说次级路径辨识时激励源噪声选择问题，滤波器阶数等诸多问题的选择和优化。

---

一、次级路径的辨识

在主动降噪开发之一中并未考虑次级次级路径的问题，但在实际中，扬声器到麦克风之间是存在一定的距离，扬声器到我们耳朵之间也存在一定的距离，那么声音在传播的过程中就会存在一定的衰减。
假设，传递路径上的传递函数为h(t)，那么在扬声器输出的信号f(t)和mic接收到的信号g(t)就存在以下关系：
g(t) = f(t)*h(t)
两者为卷积的关系，表现在频域上就是相乘。那么问题来了，怎么获得g(t)??，其准确性对后续噪声的控制影响极大。目前存在三种激励方式，分别为白噪声，线性正弦扫频和指数正弦扫频，白噪声自不用说，后两者对应的频谱如下：
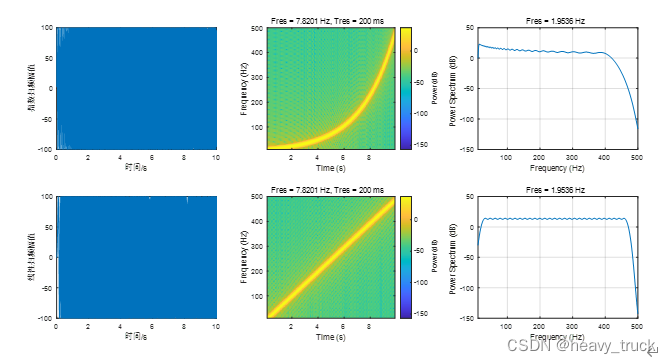实际上，根据人耳朵的声学特性，更符合指数正弦臊扫频，但在实际应用中会根据实际情况（扬声器频响，时间的长短，降噪频带范围等）进行选择，一般来说，白噪声的频谱更为丰富，所需激励时间也较短，得到的响应也含有较为丰富发频谱特性，应用较广。
部分代码如下：

%% 线性扫频
t1 = 1/fs:1/fs:t0;
y2 = chirp(t,0,10,500,'quadratic'); % 自带程序生成的扫频；
beta = (endFre-startFre)/t0;
y1 = A*sin(2*pi*(0.5*beta*t1.^2+startFre*t1));
subplot(131)
plot(t1,y1)
xlabel('时间/s')
ylabel('线性扫频幅值')
subplot(132)
pspectrum(y1,fs,'spectrogram','FrequencyLimits',[10 1000],'TimeResolution',0.2, ...
    'OverlapPercent',99,'Leakage',0.85)
subplot(133)
pspectrum(y1,fs,'FrequencyLimits',[10 1000])

二、滤波器阶数的选择

根据激励得出的响应，计算出对应的传递函数，这其实有两种方法，第一，分别计算对应的频谱特性，然后再逆傅里叶变化，第二，就是采样LMS算法进行辨识，这是最简单和最方便的，效率最高的一种方法，这两种方法辨识的结果如下：
可见，其前128阶趋势基本一致，相对而言，LMS识别出的冲激响应幅值较大，而反变换则在0处存在一个极大值，这主要是由于信号存在直流分量引起的（经过大神指导，该该处存在的极大值并不是直流分量引起，而是由极值点引起），需要在实际中进行甄别。
对识别出的传递函数的阶数需要进行优化，优化的前提就是根据实际硬件的承受能力，也就是算力的问题，毕竟阶数越大，延迟就会越大，DSP在计算FIR滤波器时需要的时间就越长，功耗也很大。不同滤波器阶数的比较：

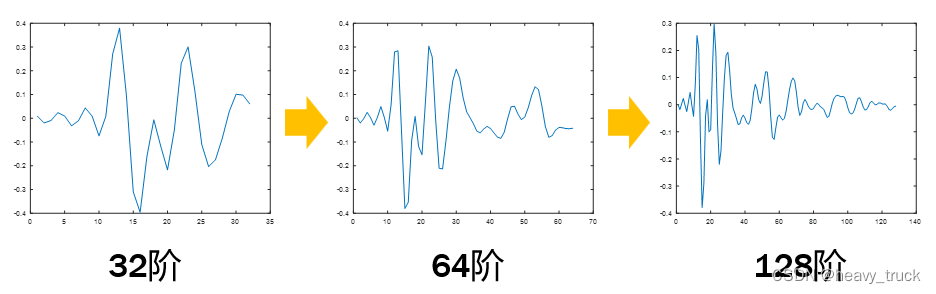
部分代码：

% 初始化参数
en = zeros(itr,1);             % 误差序列,en(k)表示第k次迭代时预期输出与实际输入的误差
W  = zeros(M,itr);             % 每一行代表一个加权参量,每一列代表-次迭代,初始为0

% 迭代计算
for k = M:itr                  % 第k次迭代,保证输入延迟后的信号有效，只有iter-M次迭代；
    x = xn(k:-1:k-M+1);        % 将输入信号延迟，使得滤波器的每个抽头都有输入
    y = W(:,k-1).' * x;        % 滤波器的输出
    en(k) = dn(k) - y ;        % 第k次迭代的误差 
    % 滤波器权值计算的迭代式
    W(:,k) =0.9* W(:,k-1) - 2*mu*en(k)*x ; % 滤波器系数更新向量,0.9的系数可以防止泄露；
end

三、多通道算法

3.1、陷波滤波器

为什么会提到这滤波器？？？，主要是因为噪声主动控制，特别是对于发动机噪声主动控制技术，主要应用的是窄带技术，简单来说就是对单个频率进行控制，那么陷波滤波器对应的频响为：

对应的特性在点击这里讲的更清楚。
那么，既然是对单个频率进行处理，我们应该怎么模拟这个信号呢，那肯定是正余弦信号，我们都知道任何信号都是有正余弦信号叠加而成，只要能够叠加出对应的频率就可以。

3.2、多通道算法

解决上述问题之后，已经完成80%，剩下的只剩20%了，现实告诉我们，任何事都存在二八分成，而这个“二”是占比最大的，那当然是最重要的了，多通道算法一般采用下面的框图：
说简单，其实也简单，就是把向量数据转换为矩阵数据而已。那么对于发动机噪声，对应的结果为：
所控制的30Hz，130Hz和195Hz都实现了峰值降低的目的，总声压OA由53.43dB降到52.39dB。

部分代码如下：

clc
clear
close all
opengl software
% load Sn.mat
load DsIdle.mat % 第一个通道；
load PsIdle.mat % 第二个通道； 通道的个数可以根据实际情况（需要降噪的个数进行添加）进行添加。
load IRF_GLOBAL_1.mat
%%
% Signal = Idle(1:end,2);
t = DsIdle(1:40960,1);
Sn1 = IRFGlobal(1:128)'; % 主驾传递函数，存在4个扬声器
Sn2 = IRFGlobal(129:256)';
Sn3 = IRFGlobal(257:384)';
Sn4 = IRFGlobal(385:512)';
Ps1 = IRFGlobal(513:640)'; % 副驾传递函数，存在4个扬声器；
Ps2 = IRFGlobal(641:768)';
Ps3 = IRFGlobal(769:896)';
Ps4 = IRFGlobal(897:1024)';
fs = 40960;
f1 = 32.5; % 目标频率1；
f2 = 130;  % 目标频率2；
f3 = 195;  % 目标频率3；
mu1 = 0.005; % 通过调节这些参数可以优化降噪后的效果；
mu2 = 0.00082; % 分别对应不同的阶次收敛步长；
mu3 = 0.00081;% 可以根据实际情况进行调整；
M = 128; % 滤波器阶数；
% t = 0:1/fs:11;
x1 = sin(2*pi*f1*t);
x2 = sin(2*pi*f2*t);
x3 = sin(2*pi*f3*t);

---

总结

由于这是一个综合多学科问题，噪声主动控制技术在实际的应用中不仅存在上述问题，最主要还有硬件性能的问题，包括扬声器频响，DSP芯片算力问题，AD、DA 转换问题。