90%的程序员写不出一个没有BUgd的二分查找的程序

 90％程序员写不出无BUG的二分查找程序？

相关文章链接如下：

• 微软过桥问题与测试人员素养
• 等价类分法 新解
• 测试用例设计中的NP难题
• 测试驱动需求分析--需求文档评审实例
• C/C++代码检视实例

《编程珠玑》（第二版）一书第四章中提及过100多名专业程序员使用两个小时的充足时间编写一个简单的二分查找程序，结果发现90％的人编出的代码都有BUG，Knuth也在他的《Sorting and Searching》一书中提过，第一个二分查找程序在1946年已经公布，但是到了1962年才出现第一个没有BUG的二分查找程序，期间经历了16年的时间。那么为什么一个简单的二分查找程序会这么容易出错呢？看一看有序表的查找的测试用例设计也许能明白为什么。

要对有序表查找进行用例设计，我们可以先分析输入域，实际上有两个输入域，一个是要查找的数据，另外一个是有序表，可以先对有序表数据的个数进行分类，有序表中可能有0，1，2，3，…个数据。因此我们可以将目标数据分为以下几个类：

 

完成第1级分类后，我们可以再对数据的特点进行分类，因为有序表是一个有顺序的表，是有大小顺序的，因此可以根据数据特点再进行分类，以3个数据为例可以进行以下分类：

有序表有0、1、2、4个以上数据的情况都可以按照以上的类似的方式进行再分类。

当按有序表中分类好后，可以再按要查找的数据进行分类

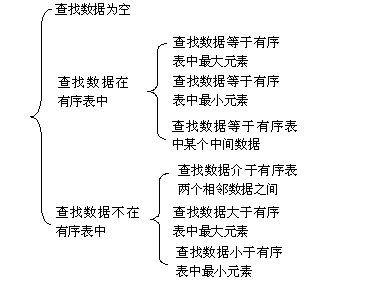
当对查找的数据和有序表分别分好类后，就可以把这两种分类组合起来，比如将有序表有3个数据的分类情况和查找数据的分类情况组合起来就可以得到以下的分类：

 

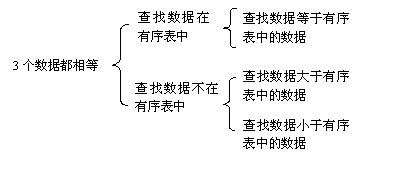
组合完后，还需要将一些不可能或不需要的组合删除掉，比如在3个数据都相等的情况下，查找数据介于集合两个相邻数据之间的情况就不存在，需要删除掉这种情况，查找数据在有序表中的3种分类也由于集合中数据都相等而变成了一个分类，下图便是3个数据都相等情况下的一个分类： 

这样7个最终分类减少到只有4个最终分类，查找数据为空的情况并不是所有情况下都需要测试的，其实只要测试有序表中有数据和没有数据两种情况就够了，因此查找数据为空的情况如果在其他情况中有了分类，那么也可以将其删去，这样3个数据都相等的情况就只有3个最终分类，如下图所示： 

有序表有0个数据时可以所见成测试两种情况，一种是查找的数据为空，一种是查找的数据不为空。 

有序表中有1个数据时的分类可以缩减成以下3种分类情况： 

 

有序表中有2个数据的分类可以缩减成以下8种分类： 

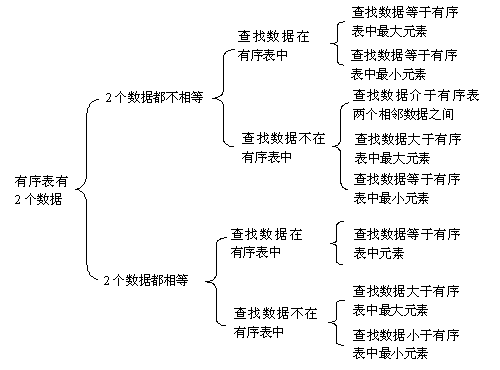
这样一来，即使不考虑4个以上数据以及3个数据在有两个数据相等情况下的分类，总共的最终分类也有20多种，每种分类至少需要设计一个测试用例，总共至少需要20多个测试用例，一个简单的二分查找的测试用例都至少需要20多个，看到这里大家也许会明白为什么90％的专业程序员写不出一个无BUG的二分查找程序来。