Codeforces E. Permutation Separation

类似二维偏序

题意：

给定$1$到$n$的一个排列$p_1,p_2,...,p_n$，移动花费$a_i$。

求

1. 先将排列划分为两个非空集合——$p_1,p_2,...p_k$和$p_{k+1},p_{k+1},..p_n$，$1\le k<n$。
2. 再移动元素$p_i$，使得最终前面的集合$s_1$中的元素都小于后面的集合$s_2$中的元素，$s_1,s_2$可为空， m a x { s 1 } = y , ∀ { s 2 } > y max\{s_1\}=y,\forall\{s_2\}>y max{s1​}=y,∀{s2​}>y

的最小花费。

INPUT
n = 6
p = [ 3 5 1 6 2 4 ]
a = [ 9 1 9 9 1 9 ]
OUTPUT
2

解析：

如果确定分开的位置$k=x$，和临界值$y$（$x\in [1,n-1],y\in [1,n]$），则需要付出的代价为
$$\sum _{i\le x,p_i>y}{a}_i+\sum _{i>x,p_i\le y}{a}_i,i\in [1,n]$$
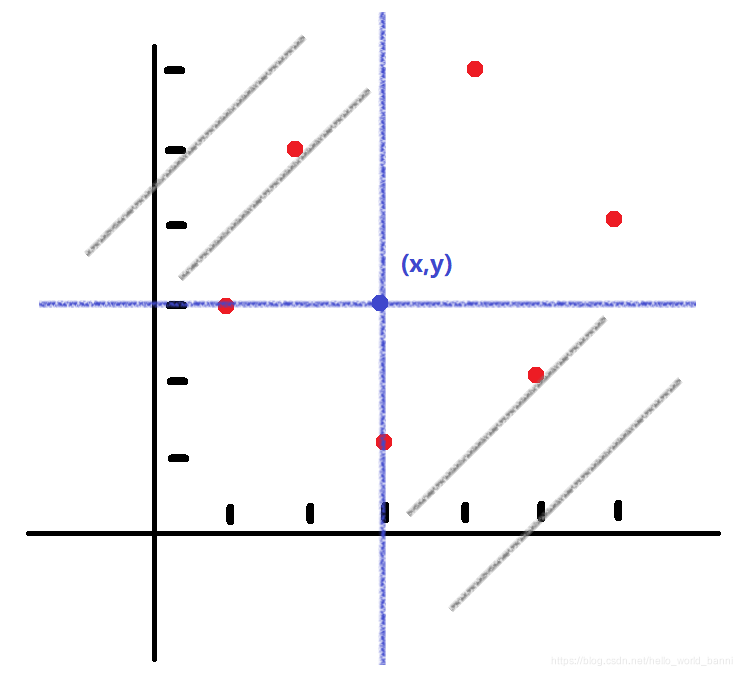
将排列中的每个元素看作二维平面上的点$(i,p_i)$，及要求一个点$(x,y)$，使得在点$(x,y)$左上和右下角的元素权值和最小。

如何快速的遍历所有的$(x,y)$组合呢？

暴力枚举的计算空间为$n\ast n$，对于每个$(x,y)$组合的查询复杂度是$O(n)$，总的复杂度是$O(n^3)$，是不成立的。

根据二维偏序类问题的一般解题方法，固定一个维度枚举，另一个维度做区间修改，达到总体$O(n\log n)$的复杂度。

我们可以维护的区间为$x$轴，因为属性$a_i$是在$x$轴上的，我们区间修改只能该$x$轴吗，所以枚举$y$轴。

如何初始化呢？$y=0$时，就相当于全都移到了右边，$\forall (i,p_i),p_i>0$，所以对所有$x$，满足$i\le x$的点都会对$(x,y=0)$产生贡献，发现这就是一个前缀和。

观察可知，当$y$轴增加$1$时，每次对之前的值改变的只有$(i,p_i=y)$个点。对于每个$x$，看它与$(i,p_i=y)$的关系，如果$(i,p_i=y)$在$x$的左下角（就是$i<x$），贡献就还没有算要增加$a_i$，在$x$的右下角（就是$i\ge x$），贡献就多算了要减掉$a_i$。

当前$y$，区间$[1,n-1]$的最小值就是当前$y$与$\forall x$组合的最小值。

最终线段树维护的是区间最小值，实现的就是区间修改和区间查询。

/*
* @Author: XiaoBanni
* @Email:  xjc5069@gmail.com
* @Date:   2020-02-02 19:16:29
* @Last Modified by:   Y
* @Last Modified time: 2020-02-08 12:15:33
*/

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF=INT_MAX/2;
const ll LLINF=9223372036854775807/2;
#define in(a) scanf("%d",&a)
#define inll(a) scanf("%lld",&a)
#define outln(a) printf("%d\n",a)
#define outllln(a) printf("%lld\n",a)
#define fin(i,st,n) for(int i=st;i<n;i++)
#define fin2(i,st,n) for(int i=st;i<=n;i++)

//定义************
#define maxn 200007  //元素总个数
ll Add[maxn<<2];//Sum求和，Add为懒惰标记 
ll A[maxn],n;//存原数组数据下标[1,n] 
ll Min[maxn<<2];

//====================================
//建树

//PushUp函数更新节点信息 ，这里是求和
void PushUp(int rt){
	Min[rt]=min(Min[rt<<1],Min[rt<<1|1]);
}
//Build函数建树 
void Build(int l,int r,int rt){ //l,r表示当前节点区间，rt表示当前节点编号
	if(l==r) {//若到达叶节点 
		Min[rt]=A[l];
		return;
	}
	int m=(l+r)>>1;
	//左右递归 
	Build(l,m,rt<<1);
	Build(m+1,r,rt<<1|1);
	//更新信息 
	PushUp(rt);
}

//======================================
//下推标记

void PushDown(int rt,int ln,int rn){
	//ln,rn为左子树，右子树的数字数量。 
	if(Add[rt]){
		//下推标记 
		Add[rt<<1]+=Add[rt];
		Add[rt<<1|1]+=Add[rt];
		//修改子节点的Min使之与对应的Add相对应 
		Min[rt<<1]+=Add[rt];
		Min[rt<<1|1]+=Add[rt];
		//清除本节点标记 
		Add[rt]=0;
	}
}

//=======================================
//区间修改

void Update(int L,int R,int C,int l,int r,int rt){//L,R表示操作区间，l,r表示当前节点区间，rt表示当前节点编号 
	if(L <= l && r <= R){//如果本区间完全在操作区间[L,R]以内
		Add[rt]+=C;//增加Add标记，表示本区间的Sum正确，子区间的Sum仍需要根据Add的值来调整
		Min[rt]+=C;
		return ; 
	}
	int m=(l+r)>>1;
	PushDown(rt,m-l+1,r-m);//下推标记
	//这里判断左右子树跟[L,R]有无交集，有交集才递归 
	if(L <= m) Update(L,R,C,l,m,rt<<1);
	if(R >  m) Update(L,R,C,m+1,r,rt<<1|1); 
	PushUp(rt);//更新本节点信息 
} 

//=======================================
//区间查询

ll Query(int L,int R,int l,int r,int rt){//L,R表示操作区间，l,r表示当前节点区间，rt表示当前节点编号
	if(L <= l && r <= R){
		//在区间内，直接返回 
		return Min[rt];
	}
	int m=(l+r)>>1;
	//下推标记，否则Sum可能不正确，因为在Update((L <= l && r <= R))中的还没有根据标记更新
	PushDown(rt,m-l+1,r-m); 
	
	//累计答案
	ll ANS=LLINF;
	if(L <= m) ANS=min(ANS,Query(L,R,l,m,rt<<1));
	if(R >  m) ANS=min(ANS,Query(L,R,m+1,r,rt<<1|1));
	return ANS;
} 

//========================================
//函数调用

	// //建树 
	// Build(1,n,1); 
	// //点修改
	// Update(L,C,1,n,1);
	// //区间修改 
	// Update(L,R,C,1,n,1);
	// //区间查询 
	// int ANS=Query(L,R,1,n,1);

int p[maxn],a[maxn];
int main(){
	in(n);
	fin2(i,1,n){
		int ans;
		in(ans);
		p[ans]=i;
	}
	fin2(i,1,n){
		in(a[i]);
		A[i]=A[i-1]+a[i];
	}
	memset(Min,0x3f3f3f3f,sizeof(Min));
	Build(1,n,1);
	ll ANS=Query(1,n-1,1,n,1);
	for(int y=1;y<=n;y++){
		int pi=p[y];
		if(pi-1>=1) Update(1,pi-1,a[pi],1,n,1);
		Update(pi,n,-a[pi],1,n,1);
		ANS=min(ANS,Query(1,n-1,1,n,1));
	}
	outllln(ANS);
}

题目链接