力扣-108. 将有序数组转换为二叉搜索树-CPP_把数组排成二叉搜索树c++-CSDN博客

本文链接：https://blog.csdn.net/hengbao4/article/details/122168141

0.前言

有了之前的对于二叉树的简单准备，我终于有信心开启这个的讲解。我不再贴出自己的解法，我们直接讲解官方题解。

1.官方题解

class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return helper(nums, 0, nums.size() - 1);
    }

    TreeNode* helper(vector<int>& nums, int left, int right) {
        if (left > right) {
            return nullptr;
        }

        // 总是选择中间位置左边的数字作为根节点
        int mid = (left + right) / 2;

        TreeNode* root = new TreeNode(nums[mid]);
        root->left = helper(nums, left, mid - 1);
        root->right = helper(nums, mid + 1, right);
        return root;
    }
};

官方题解的思路很简单，就是要每次递归生成一个子树部分。

1.1.仅切割中点

但其实，第一次做这个题目，我们是想不到这么流畅，我们只能先想出错误的解法，就像下面这样：

		int mid = (left+right)/2;
		treeNode->left = helper(nums,left,mid);
		treeNode->right = helper(nums,mid,right);
		return treeNode;

在这段代码里，我们看到了什么呢？有切割中点的思路，知道要左右子树去分别递归，但是这么写。总觉得少了点什么，接下来，我们以 [0,1,2,3] 为例，一步一步接近正确的解题思路。

因为数组的下标是从0开始的，所以这里我们为了保持一致，一直使用数组下标进行表示。

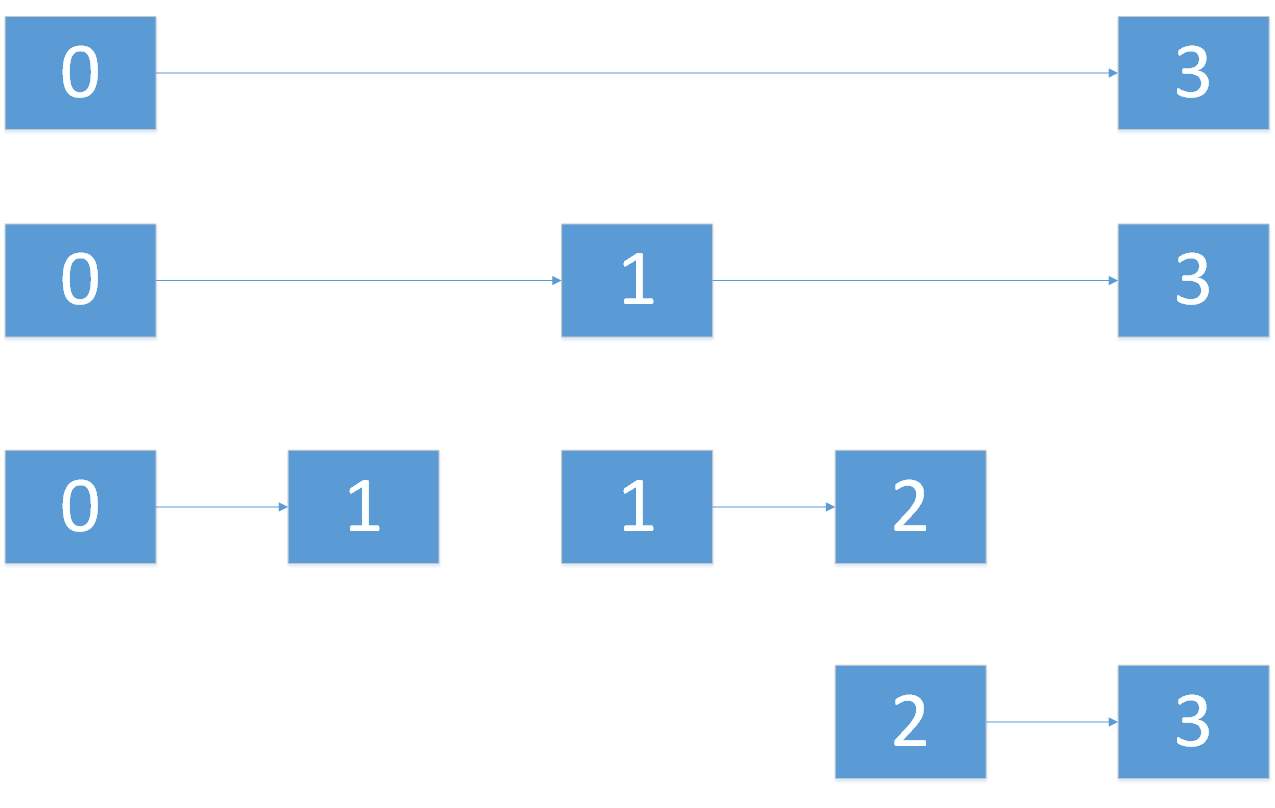
仅仅切割中点
我们发现，当我们持续向下分割，分割到[0,1] [1,2] [2,3] 时，程序无法再分割下去了。

因为我们只进行了分割，没有去创建这棵树。

1.2.创建根节点

那么，我们该怎么办呢？我们要把每个根节点给它创建出来啊。

		int mid = (left+right)/2;
		TreeNode* root = new TreeNode(nums[mid]);
		treeNode->left = helper(nums,left,mid);
		treeNode->right = helper(nums,mid,right);
		return treeNode;

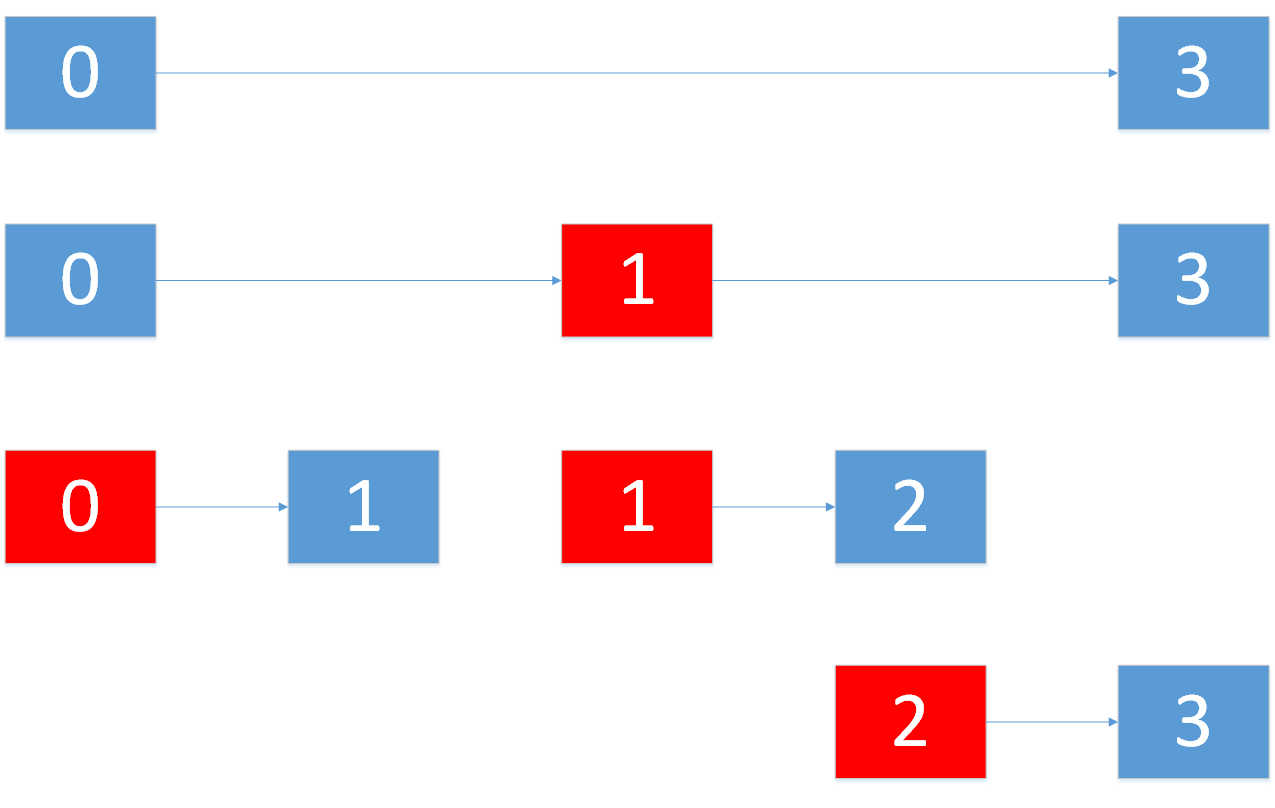
请添加图片描述

1.3.走出重复创建的怪圈

我们发现还是不对，根节点在上一次已经创建出来了，下一次递归时，它又创建了。

我们发现如果我们持续传入mid对应的数据，它就会一直存在着。然后不停地在计算mid的过程中被计算出来。

这样就一直创建相同的值的根节点了，这可不行，我们下一次传入的时候不能再要这个位置。

        int mid = (left + right) / 2;

        TreeNode* root = new TreeNode(nums[mid]);
        root->left = helper(nums, left, mid - 1);
        root->right = helper(nums, mid + 1, right);
        return root;

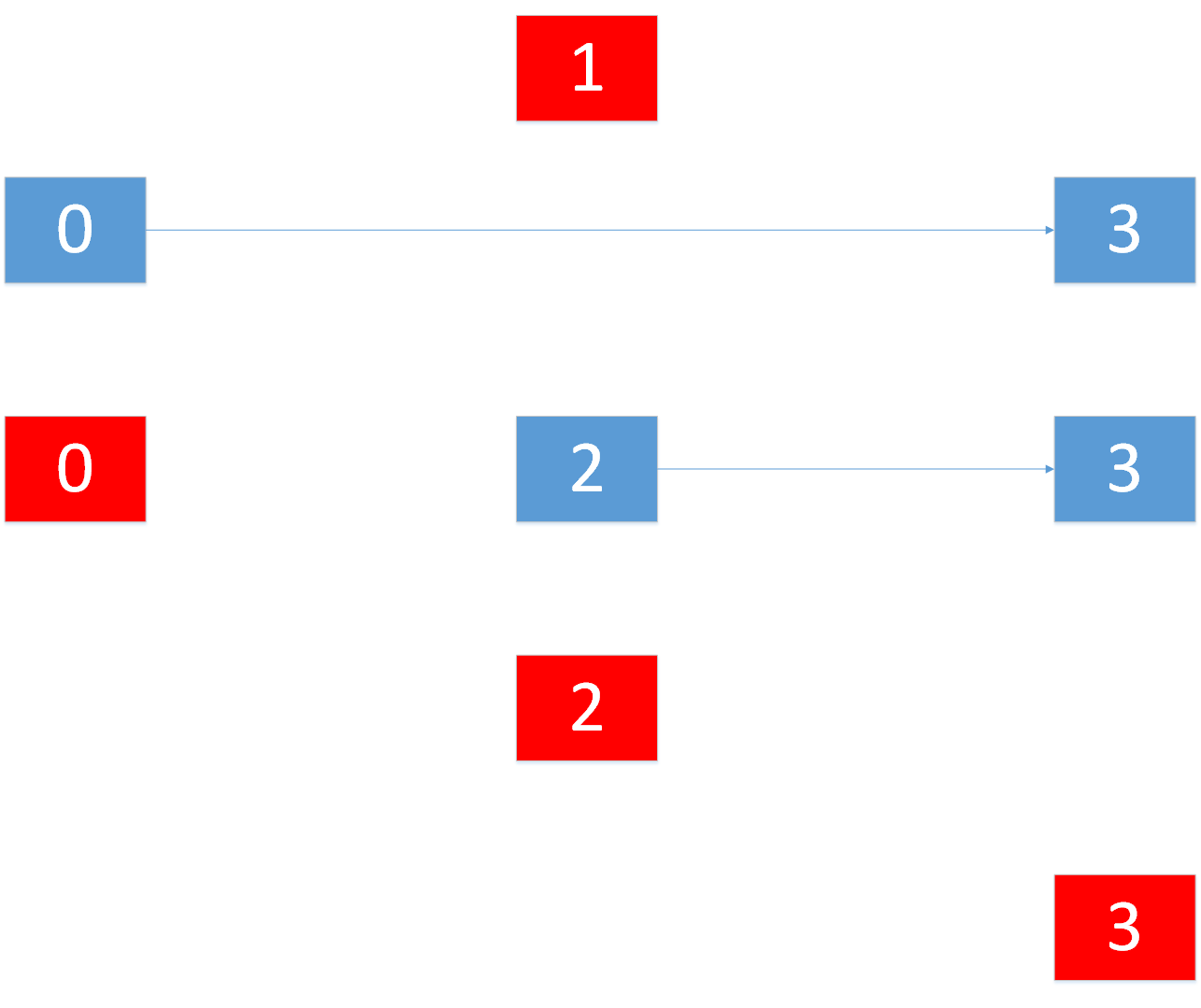
只创建根节点

1.4.补足临界条件

现在我们的关键的节点已经能连接上了，但是有个问题，最后的叶子结点，左右子树应该为NULL，如何判断我们递归到了叶子结点呢？

我们发现啊，有两种情况，我们会创建一个结点：

当 $\lt right$ 时，我们取 $\left \lfloor {\frac{left + right}{2}} \right \rfloor$ ，此时创建 $m i d$ 。
当 $l e f t = r i g h t$ 时，我们取上式时，其实就是直接取 $l e f t$ 或 $r i g h t$ 。

除此之外的情况，我们应该都是为NULL的情况，故得：

class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return helper(nums, 0, nums.size() - 1);
    }

    TreeNode* helper(vector<int>& nums, int left, int right) {
        if (left > right) {
            return nullptr;
        }

        // 总是选择中间位置左边的数字作为根节点
        int mid = (left + right) / 2;

        TreeNode* root = new TreeNode(nums[mid]);
        root->left = helper(nums, left, mid - 1);
        root->right = helper(nums, mid + 1, right);
        return root;
    }
};