Matlab单相PWM逆变仿真与滤波设计

基于Matlab的单相正弦波PWM逆变电路仿真及滤波器设计

1 引言

在电力电子技术中，将直流电转换为交流电称为逆变。逆变电路应用广泛，例如当直流电源供电给交流负载时就需要逆变电路。逆变电路也是交流电机调速用变频器、不间断电源和感应加热电源等电力电子装置的核心部分[1]。

目前，逆变技术主要采用脉宽调制（PWM）。由于PWM波的特性决定了功率放大装置的输出电压含有较多的谐波成分[2]，因此必须在逆变器输出端使用滤波器，以使输出波形达到平滑正弦波形，并减少谐波对负载的影响。

2 单相正弦波PWM逆变电路仿真

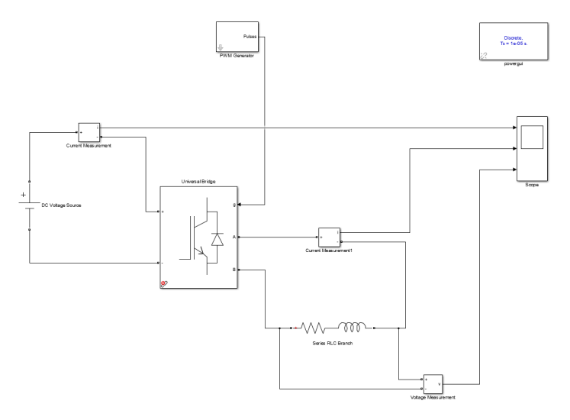
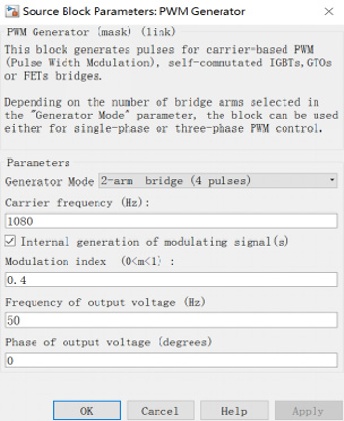
基于单极性PWM调制的单相正弦波逆变电路的仿真模型如图1所示。主电路中的直流电源电压为200 V，通过由通用桥模块[3]构成的桥式逆变电路连接至阻感负载。负载电感为2mH，电阻为3Ω。

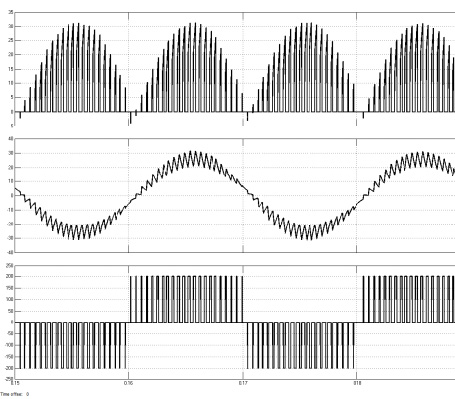
3 滤波器设计

3.1 滤波器参数设置

在设计滤波器时，通常先设计电感L的取值。电感的选择与纹波电流和系统的功耗有关。一般情况下，电感L上的纹波电流选取为额定电流的15%–25%。

在单极性调制[4]的情况下：

$$
\Delta I_l = \frac{U_d - U_o(t)}{L} \cdot D(t) \cdot T_e
$$

在开关频率远大于工作频率的条件下，根据单极性PWM原理，可得到每个开关周期的占空比如下

$$
D(t) = \frac{U_o(t)}{U_d}
$$

将公式(2)代入公式(1)可得

$$
\Delta I_l = \frac{U_d - U_o(t)}{L} \cdot \frac{U_o(t)}{U_d} \cdot T_e
$$

As can be seen from equation (3), 当 $2U_o(t) = U_d$ 时，达到最大值

$$
\Delta I_{l\text{max}} = \frac{U_d}{4Lf_c}
$$

因此有

$$
L \geq \frac{U_d}{4f_c \Delta I_{l\text{max}}}
$$

The cut-off frequency of LC filter $f_c$ is

$$
f_c = \frac{1}{2\pi\sqrt{LC}}
$$

among them

$$
f_h \leq f_c \leq 10f_{\text{min(har)}}
$$

In the formula: $f$ the fundamental 频率；$(min)harf$ 是最低谐波频率。

如果将滤波电感L的电流纹波近似视为正弦波，并假设所有电流纹波均由滤波电容C吸收，则输出电压纹波的最大值应为

$$
\Delta U_{o\text{max}} = \frac{\Delta I_{l\text{max}}}{2\pi f_c C}
$$

公式(4)代入公式(7) can be obtained by substituting

$$
\Delta U_{o\text{max}} = \frac{U_d}{8\pi^2 f_c^2 LC}
$$

获取 following equation

$$
LC \geq \frac{U_d}{8\pi^2 f_c^2 \Delta U_{o\text{max}}}
$$

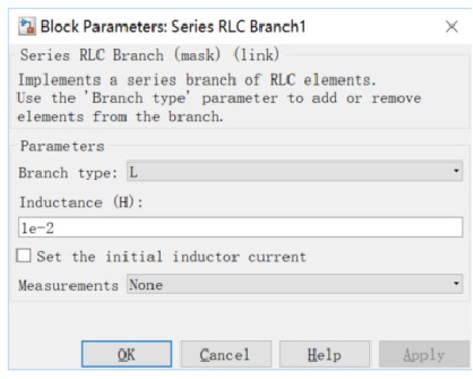
电感L的值可根据公式(5)确定，电容C的值可由公式(6)计算得出。电感L的参数设置如图4所示，电容C的参数设置如图5所示。

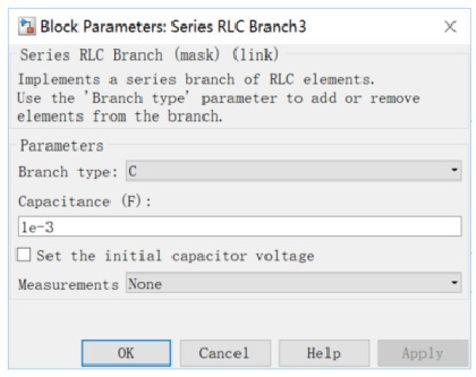
3.2 仿真模型的建立

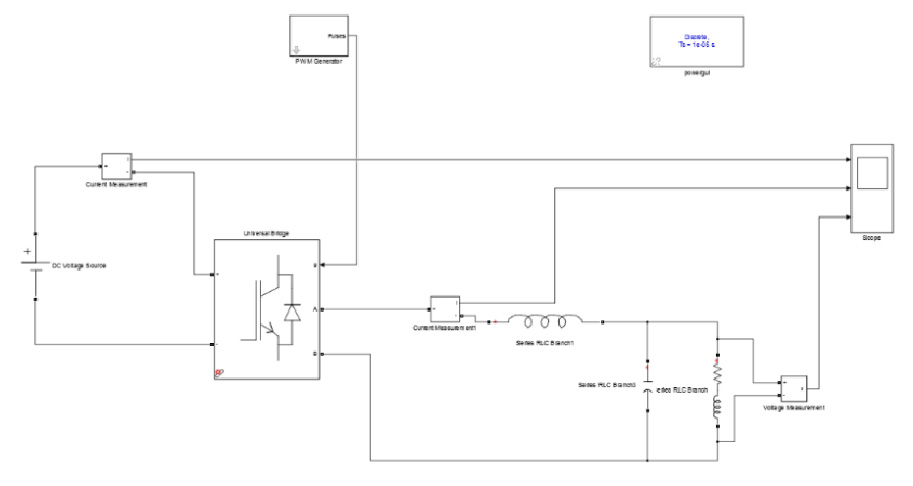
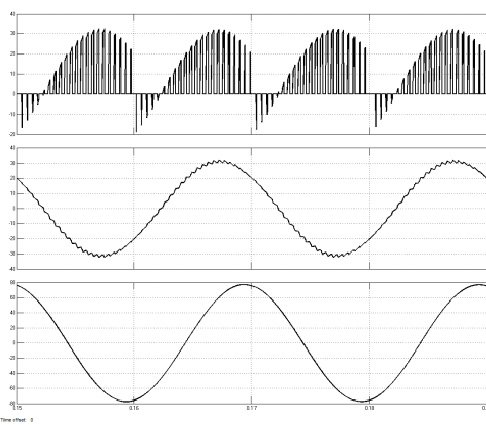
LC滤波器的仿真电路如图6所示，输出波形如图7所示。

4 谐波分析

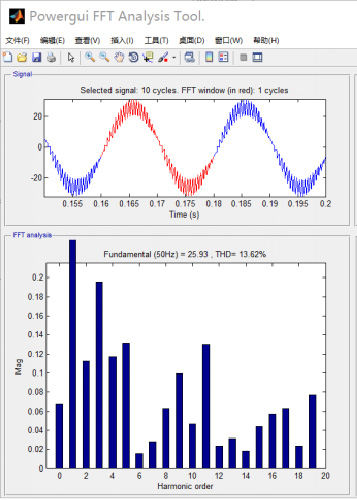
通过“功率GUI”对未加滤波器的单相正弦PWM逆变电路所获得的输出电流进行谐波分析，结果如图8所示。总谐波畸变率= 13.62 %，远大于国家标准[5]规定的8 %。

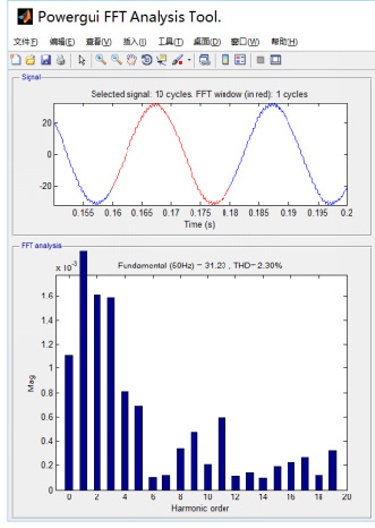
通过单相正弦PWM逆变电路经过滤波器滤波后，通过功率GUI进行分析，结果如图9所示。总谐波畸变率= 2.30%，大大降低了谐波含量，符合国家标准。

5 结论

为了使PWM逆变器具有更好的输出波形，针对PWM逆变器的高谐波频率，采用了二阶LC低通滤波网络[6]。

从仿真结果可以看出，加入LC滤波后，输出电压中的谐波成分被滤除，更接近正弦波形，同时负载电流的波形更加平滑，正弦度更好。这表明增加滤波环节能明显改善逆变器输出波形。