HDU 6050

Funny Function

                                                                 Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
                                                                                           Total Submission(s): 350    Accepted Submission(s): 149

Problem Description

Function  Fx,y satisfies:

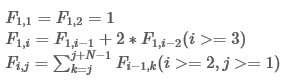
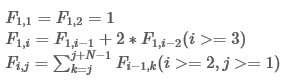
For given integers N and M,calculate  Fm,1  modulo 1e9+7.

 

Input

There is one integer T in the first line.
The next T lines,each line includes two integers N and M .
1<=T<=10000,1<=N,M<2^63.

 

Output

For each given N and M,print the answer in a single line.

 

Sample Input

  
  

   
   2
2 2
3 3
  
  

 

Sample Output

  
  

   
   2
33
  
  

 

Source

2017 Multi-University Training Contest - Team 2

 

解题思路：题意就不解释了，根据题目里给的式子去求，现场赛的时候两个队友一直用excel在那里找规律，最后找出了奇数和偶数时不同的递推式：

奇数：F（m，1）=F（m-1，1）*（2^n-1）-C（n/2），C（x）=C（x-1）*4+2

偶数：F（m，1）=（2^n-1）^（m-1）/3

然后矩阵快速幂搞一下就好了，奇数的时候最后答案要乘2

官方题解：

对于任意i>=1，当j>=3时，有 通过归纳法可以得到

  进而推导出 通过矩阵快速幂求解

[cpp] view plain copy

print ?

1. #include <iostream>    
2. #include <cstdio>    
3. #include <cstring>    
4. #include <string>    
5. #include <algorithm>    
6. #include <map>    
7. #include <cmath>  
8. #include <set>    
9. #include <stack>    
10. #include <queue>    
11. #include <vector>    
12. #include <bitset>    
13. #include <functional>  
14.   
15. using namespace std;  
16.   
17. #define LL long long    
18. const int INF = 0x3f3f3f3f;  
19. const LL mod = 1000000007;  
20.   
21. LL n, m;  
22.   
23. struct Matrix  
24. {  
25.     LL v[9][9];  
26.     Matrix()  
27.     {  
28.         memset(v, 0, sizeof v);  
29.     }  
30. } dan;  
31.   
32. Matrix mul(Matrix a, Matrix b, int d)  
33. {  
34.     Matrix ans;  
35.     for (int i = 0; i < d; i++)  
36.     {  
37.         for (int j = 0; j < d; j++)  
38.         {  
39.             for (int k = 0; k < d; k++)  
40.             {  
41.                 ans.v[i][j] += (a.v[i][k] * b.v[k][j]) % mod;  
42.                 ans.v[i][j] %= mod;  
43.             }  
44.         }  
45.     }  
46.     return ans;  
47. }  
48.   
49. Matrix qpow(Matrix a, LL k, int d)  
50. {  
51.     Matrix ans = dan;  
52.     while (k)  
53.     {  
54.         if (k & 1) ans = mul(ans, a, d);  
55.         k >>= 1;  
56.         a = mul(a, a, d);  
57.     }  
58.     return ans;  
59. }  
60.   
61. LL qpow(LL x, LL y)  
62. {  
63.     LL ans = 1;  
64.     while (y)  
65.     {  
66.         if (y & 1) ans *= x, ans %= mod;  
67.         y >>= 1;  
68.         x *= x;  
69.         x %= mod;  
70.     }  
71.     return ans;  
72. }  
73.   
74. LL extend_gcd(LL a, LL b, LL &x, LL &y)  
75. {  
76.     if (!b)  
77.     {  
78.         x = 1, y = 0;  
79.         return a;  
80.     }  
81.     LL gcd = extend_gcd(b, a%b, x, y);  
82.     LL tmp = x;  
83.     x = y;  
84.     y = tmp - (a / b)*y;  
85.     return gcd;  
86. }  
87.   
88. int main()  
89. {  
90.     int t;  
91.     scanf("%d", &t);  
92.     while (t--)  
93.     {  
94.         scanf("%lld%lld", &n, &m);  
95.         if (m == 1) { printf("1\n"); continue; }  
96.         Matrix a, ans;  
97.         LL ans1 = (qpow(2, n) - 1 + mod) % mod;  
98.         if (n % 2)  
99.         {  
100.             dan.v[0][0] = 0, dan.v[0][1] = 1;  
101.             a.v[0][0] = 4, a.v[0][1] = 0, a.v[1][0] = 2, a.v[1][1] = 1;  
102.             ans = qpow(a, n / 2, 2);  
103.             dan.v[0][0] = 1, dan.v[0][1] = 1;  
104.             a.v[0][0] = ans1, a.v[0][1] = 0, a.v[1][0] = -ans.v[0][0], a.v[1][1] = 1;  
105.             ans = qpow(a, m - 1, 2);  
106.             printf("%lld\n", (ans.v[0][0]+mod)%mod);  
107.         }  
108.         else  
109.         {  
110.             ans1 = qpow(ans1, m - 1);  
111.             LL x, y;  
112.             extend_gcd(3, mod, x, y);  
113.             ans1 = ans1*x%mod;  
114.             ans1 = (ans1 * 2) % mod;  
115.             printf("%lld\n", ans1);  
116.         }  
117.     }  
118.     return 0;  
119. }  

#include <iostream>  
#include <cstdio>  
#include <cstring>  
#include <string>  
#include <algorithm>  
#include <map>  
#include <cmath>
#include <set>  
#include <stack>  
#include <queue>  
#include <vector>  
#include <bitset>  
#include <functional>

using namespace std;

#define LL long long  
const int INF = 0x3f3f3f3f;
const LL mod = 1000000007;

LL n, m;

struct Matrix
{
    LL v[9][9];
    Matrix()
    {
        memset(v, 0, sizeof v);
    }
} dan;

Matrix mul(Matrix a, Matrix b, int d)
{
    Matrix ans;
    for (int i = 0; i < d; i++)
    {
        for (int j = 0; j < d; j++)
        {
            for (int k = 0; k < d; k++)
            {
                ans.v[i][j] += (a.v[i][k] * b.v[k][j]) % mod;
                ans.v[i][j] %= mod;
            }
        }
    }
    return ans;
}

Matrix qpow(Matrix a, LL k, int d)
{
    Matrix ans = dan;
    while (k)
    {
        if (k & 1) ans = mul(ans, a, d);
        k >>= 1;
        a = mul(a, a, d);
    }
    return ans;
}

LL qpow(LL x, LL y)
{
    LL ans = 1;
    while (y)
    {
        if (y & 1) ans *= x, ans %= mod;
        y >>= 1;
        x *= x;
        x %= mod;
    }
    return ans;
}

LL extend_gcd(LL a, LL b, LL &x, LL &y)
{
    if (!b)
    {
        x = 1, y = 0;
        return a;
    }
    LL gcd = extend_gcd(b, a%b, x, y);
    LL tmp = x;
    x = y;
    y = tmp - (a / b)*y;
    return gcd;
}

int main()
{
    int t;
    scanf("%d", &t);
    while (t--)
    {
        scanf("%lld%lld", &n, &m);
        if (m == 1) { printf("1\n"); continue; }
        Matrix a, ans;
        LL ans1 = (qpow(2, n) - 1 + mod) % mod;
        if (n % 2)
        {
            dan.v[0][0] = 0, dan.v[0][1] = 1;
            a.v[0][0] = 4, a.v[0][1] = 0, a.v[1][0] = 2, a.v[1][1] = 1;
            ans = qpow(a, n / 2, 2);
            dan.v[0][0] = 1, dan.v[0][1] = 1;
            a.v[0][0] = ans1, a.v[0][1] = 0, a.v[1][0] = -ans.v[0][0], a.v[1][1] = 1;
            ans = qpow(a, m - 1, 2);
            printf("%lld\n", (ans.v[0][0]+mod)%mod);
        }
        else
        {
            ans1 = qpow(ans1, m - 1);
            LL x, y;
            extend_gcd(3, mod, x, y);
            ans1 = ans1*x%mod;
            ans1 = (ans1 * 2) % mod;
            printf("%lld\n", ans1);
        }
    }
    return 0;
}