费马素性测试和米勒—拉宾素性测试

最新推荐文章于 2021-11-13 14:23:51 发布

hexianhao

最新推荐文章于 2021-11-13 14:23:51 发布

阅读量2.7k

点赞数 1

分类专栏：数学文章标签：数学

数学专栏收录该内容

45 篇文章 1 订阅

订阅专栏

chapter 1

Fermat's little theorem

费马小定理

费马小定理说的是：如果p是一个素数，那么对于任意一个整数a，a^p − a 能被p整除，也可以用模运算表示如下：

$a^p \equiv a \pmod{p}.\,\!$ （p是素数，a是整数）

这个定理又如下变式：如果p是一个素数，且整数a与p互素，那么 a^p−1 − 1 可以被p整除，用模运算表示如下

$a^{p-1} \equiv 1 \pmod{p}.\,\!$ （p是素数，a是整数，a与p互素）、

还有一种表述是：如果p是一个素数，a是一个整数且a不包含因数p，那么 a^p−1 − 1 可以被p整除。

费马小定理是费马素性测试的基础。

费马在给出此定理的时候未给出证明，第一个证明其的人是Gottfried Leibniz。

————<对于费马小定理的证明>————

对于费马小定理的证明十分多，大部分证明基于两个简化：

1.我们可以假设0 ≤ a ≤ p − 1或1 ≤ a ≤ p ，这可以由以下同余定理简单推出

若 $\left\{ \begin{matrix} a \equiv b \pmod{m} \\ c \equiv d\pmod{m} \end{matrix} \right.$ ,则 $\left\{ \begin{matrix} a \pm c \equiv b \pm d \pmod{m} \\ ac \equiv bd \pmod{m} \end{matrix} \right.$

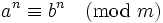
且有特别的若 $a \equiv b \pmod{m}$ ，则 $a^n \equiv b^n \pmod{m}$

2.事实上我们只要证明：

在1 ≤ a ≤ p − 1有

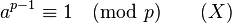
$a^{p-1} \equiv 1 \pmod p \quad \quad (X)$

若X在此时a的取值范围下成立的话，当a的0时，原始的式子就显然成立了（注意了，这样的两步化简还有效的避免了对“p与a互质”的讨论）

***关于费马小定理的一个奇妙而伟大的组合证明！！！***

这是关于费马小定理最浅显易懂的，也是最奇妙的一个证明，叫做Proof by counting bracelets，创始人是Golomb，以下是完整的证明。

已知：p是素数，a是整数且1≤ a ≤ p

求证：a^p − a 能被p整除

证明：假设又一种由p个珠子组成的项链，项链中珠子的种数为最多为a，那么所有可能的不重复的排列为a^p，其中种数为1的情况有a种，那么去除这些情况后一共就有a^p− a种。现在吧所有情况的项链首尾相接，那么就有可能出现重复的情况了。因为p是素数，所以一个包含着p个珠子的环旋转后会出现p种不同的情况（这里就不证明了，即使不是像1+1=2那么显而易见，但也是很容易证明的），亦即，这a^p− a种情况可以分为一些类，每类有p中情况，亦即，a^p − a 能被p整除。证毕

补充：一下是a=2，p=5的情况
        AAABB, AABBA, ABBAA, BBAAA, BAAAB,
        AABAB, ABABA, BABAA, ABAAB, BAABA,
        AABBB, ABBBA, BBBAA, BBAAB, BAABB,
        ABABB, BABBA, ABBAB, BBABA, BABAB,
        ABBBB, BBBBA, BBBAB, BBABB, BABBB,
        AAAAA,
        BBBBB.
        以及，当p不为素数，比如当a=2，p=12时旋转后的一个反例
        ABBABBABBABB,
        BBABBABBABBA,
        BABBABBABBAB. ——>事实情况是3种而不是12种

~~~~~~~~~~费马小定理的一个拓展~~~~~~~~~~

费马小定理在欧拉定理上得到了很好的拓展，那就是：

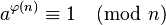
$a^{\varphi (n)} \equiv 1 \pmod{n}$

其中φ(n)表示欧拉函数，表示在1到n之间（包括1和n）与n互素的数的个数，这是一个更普遍的情况，当n=p时，其实就是费马小定理的变式了，因为此时φ(p)为p-1.

chapter 2

Fermat's primality test

费马素性测试

费马素性测试是判断一个数是否为素数的一个基于概率的测试。

事实上，费马小定理的逆否定理成立，而费马小定理的逆定理是不成立的，

而费马素性测试就是基于费马小定理的“逆定理”的。

大概的算法描述是，当p为奇数时（偶数特判一下就行啦，不就一个2嘛）让a在1-p之间(包括1和p）选取随机值，如果等式不成立，那么p肯定不是素数，如果成立，那么p就有较大可能是素数，我们称他为伪素数。

<<<<Carmichael numbers>>>>

当然，费马素性测试是有极大缺陷的，因而基本上平时没有多大用武之地。一个缺陷就是Carmichael数的存在，

Carmichael数是指如果一个数n可以通过所有‘a’值的费马素性测试却并非为素数，那么就叫n为Carmichael数。

这样的数随着n的增大而越来越少的，这些数中，最小的一个是561.

chapter 3

Miller–Rabin primality test

米勒-拉宾素性测试

/***今天的重头戏来啦！！！*/

米勒-拉宾素性测试和费马素性测试一样是一个基于概率的，判断一个数是否为素数的测试。但是作为费马素性测试的升级产品，在速度上，米勒-拉宾测试有了质的飞跃，这也就是费马素性测试当前毫无用武之地的原因了。

米勒-拉宾素性测试是当前运用最广泛的素性测试，且加上限制条件完全可以作为确定性算法。

######要讨论米勒-拉宾素性测试，首先得证明一条引理（lamma）#######

若p是一个大于2的素数，那么如果一个数与1或者-1模n同余，那么它就叫做1模n的一个非平凡的平方根。

而事实上，没有1模p的非平凡的平方根存在。

证明：假设x是一个1模p的非平凡的平方根，那么就有：

$x^{2} \equiv 1\pmod{p}$

$\left (x - 1 \right ) \left ( x + 1 \right ) \equiv 0\pmod{p}.$

因为x是非平凡的，就有（x+1）与（x-1）和x互质，就是说(x+1)和（x-1）都不能被p整除，因此（x+1)(x-1)不能被p整除，引出矛盾。

因此，没有1模p的非平凡的平方根存在。证毕

————————关键的要来啦————————————

现在我们让n为一个奇质数，而（n-1）可以表示为2^s·d的形式其中s与d都为正整数，那么根据费马小定理

$点击查看原始尺寸$ 、费马素性测试的原理，以及上面已经证明的引理可知，这个问题的关键就是，若x的平方模p为1，那么x模p得为-1或1，p才有可能为素数，否则必为合数。若x的平方模p为-1，那么x模p不作要求，那么对于任何一个，2^r·d在r不断变化得过程中必须遵循上述的规则。这样就得出了米勒-拉宾素性测试的算法：

%%%%%%%%米勒-拉宾素性测试的算法%%%%%%%%%%

判断一个数p是否为素数（p首先得为大于等于2的正整数才有可能为素数），首先判奇偶，若为偶数只有2为素数，若为奇数（这里可以考虑去掉 3甚至5的倍数），则先求出d。对于每一个底a，让d不断乘以2直到为(p-1)/2，在此过程中（包括原本的d与d=(p-1)/2时的情况），设t为 a的d次方模p的余数，（1）当t=-1时跳出，声明p有可能为素数（2）当t=1时，若d为奇数，跳出声明p有可能为素数，否则跳出声明p必为合数（3）当d=(p-1)/2时跳出，声明p必为合数。、

————————重要的要来啦————————————

要判断n是否为素数，对于一定范围内的n，只要以一定范围内a为底就可以保证这是一个确定性算法了。下面详细：

if n < 1,373,653, it is enough to test a = 2 and 3.
if n < 9,080,191, it is enough to test a = 31 and 73.
if n < 4,759,123,141, it is enough to test a = 2, 7, and 61.
if n < 2,152,302,898,747, it is enough to test a = 2, 3, 5, 7, and 11.

其中前三条应该是比较用的着的，尤其是第三条，和longint是一个数量级的！非常好用！！！

hexianhao

关注

1
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
费马素性测试和米勒—拉宾素性测试

chapter 1Fermat's little theorem 费马小定理费马小定理说的是：如果p是一个素数，那么对于任意一个整数a，a p − a 能被p整除，也可以用模运算表示如下：（p是素数，a是整数）这个定理又如下变式：如果p是一个素数，且整数a与p互素，那么 a p−1 − 1 可以被p整除，用模运算表示如下（p是素数，a是整
复制链接

扫一扫

专栏目录