零和博弈概念
二人利益对立完备信息博弈过程,在我们分析表达中就是对一个过程进行按规定双方交替操作,每次操作即搜索时选择对自己有利的情况(获益选最大,损失选最小),借助的数据结构自然是树。博弈树中每一层是某一方的走法选项。假设先手为MAX,后手为MIN。MAX可选的方案间为or关系(MAX自己掌握选项),MAX可选的方案对于可供 MIN选的方案为and关系(MAX无法决定,是MIN决定,也就是说MAX选完,MIN将自由选择)。 MAX在博弈中需要朝着自己的利益最大化出发,同时避免对自己不利的情况出现。
博弈搜索常用在棋类AI,估计最近的AlphaGo中也有它的影子。
博弈树的几点说明
1.初始状态即是初始节点(先手)。
2.博弈树的or与and节点逐层交替出现,因为二人交替出招。
3.整个博弈过程始终站在一方角度,所以可使自己胜利的结局都是本原问题,相应的节点是可解节点,所有使对方胜利的节点为不可解节点。
4.博弈树从一开始产生,他包含问题所有可能情况,但是我们在使用时,他可能并不会全部展开(生成),这取决于我们要预测多远(搜索深度)以及已经做出的操作,事实上我们在最大最小搜索中某一时期所用的搜索树只是博弈树的一部分。
极大极小搜索
基本思想
极大极小搜索(选择最好,避免最差),即为博弈搜索常用策略。
为了选择最好,避免最差,我们需要一个对于做出选择后的评估函数evaluate(),来作为我们选择的标准。假设博弈双方为MIN,MAX,规定对于有利于MAX方的态势,evaluate取正值,对于有利于MIN的evaluate取负值。对双方利益相同时evaluate取0
1.当MAX走时,MAX考虑对自己最好的情况(evaluate极大)
2.当MIN走时,MAX考虑对自己最坏的情况(evaluate极小)
3.评价往回倒推时,交替1.2来计算传递评价(通俗地讲就是生成几层搜索树,然后再依据MIN-MAX选择返回上层,由返回值决定最初的选择)
Wiki伪代码
function minimax(node, depth, maximizingPlayer) 02 if depth = 0 or node is a terminal node 03 return the heuristic value of node 04 if maximizingPlayer 05 bestValue := ?∞ 06 for each child of node 07 v := minimax(child, depth ? 1, FALSE) 08 bestValue := max(bestValue, v) 09 return bestValue 10 else (* minimizing player *) 11 bestValue := +∞ 12 for each child of node 13 v := minimax(child, depth ? 1, TRUE) 14 bestValue := min(bestValue, v) 15 return bestValue
具体表现即为下图

应用具体过程
最上层的MAX选手走,其有两种选择,每种选择后MIN选手走,最后如此重复,生成4层搜索树(这里只是向前估计2步,所以设置为4层,生成树的过程就是一个简单的广搜)。
1. 评估第四层每一个局面的评估值assessed_val,
2. 依据极大极小原则从底层返回上层(图中红色笔标记出返回路径),即MIN节点的选择其下属的节点的最小值作为自身的值,MAX选择其下属的最大的值。
3. 顶层依据返回方向,选择合理下一步,图中表现为MAX选择走左边的节点对应的那一步。
4. 重复再每一步时使用1-4的判决策略,直到某一方胜利或者平局。
井字游戏博弈代码
#include <iostream>
#include <queue>
#include <cstring>
#include <assert.h>
//MIN_MAX搜索,无Alpha与beta剪枝
using namespace std;
const int MAX_INT = 65535;
const int MIN_INT = -65535;
class ChessBoard{
short *ptr;
int how_win(int maxplayer) {
//空白全下,可胜局数
ChessBoard *tmp =new ChessBoard();
(*tmp) = (*this);
int re=0;
for(int i=0;i<cols*rows;i++) if(tmp->ptr[i]==0) tmp->ptr[i] = maxplayer;
int sum = 0;
for(int i=0;i<rows;i++) {
sum = 0;
for(int j=0;j<cols;j++) sum+=tmp->ptr[i*cols+j];
if(maxplayer==1&&sum==3) re++;
if(maxplayer==-1&&sum==-3) re++;
}
for(int i=0;i<cols;i++) {
sum = 0;
for(int j=0;j<rows;j++) sum+=tmp->ptr[j*cols+i];
if(maxplayer==1&&sum==3) re++;
if(maxplayer==-1&&sum==-3) re++;
}
sum = 0;
for(int i=0;i<rows;i++)
sum +=tmp->ptr[i*cols+i];
if(maxplayer==1&&sum==3) re++;
if(maxplayer==-1&&sum==-3) re++;
sum = 0;
for(int i=0,j=2;i<rows;i++,j--)
sum +=tmp->ptr[i*cols+j];
if(maxplayer==1&&sum==3) re++;
if(maxplayer==-1&&sum==-3) re++;
delete tmp;
return re;
}
public:
//井子棋 3*3
bool max_player; //max选手的棋局
int rows,cols;
ChessBoard *childs;
ChessBoard *next_borther;
ChessBoard *father;
int value; //评估值
ChessBoard(int rows=3,int cols=3) {
this->rows = rows;
this->cols = cols;
ptr = new short[rows*cols];
for(int i=0;i<rows*cols;i++) ptr[i] = 0;
next_borther = childs = NULL;
}
~ChessBoard() {
this->rows = 0;
this->cols = 0;
if(ptr) delete [] ptr;
ptr = NULL;
}
void operator = (ChessBoard &other) {
//复制棋盘
if(this->rows!=other.rows || this->cols != other.cols ) return ;
for(int i=0;i<rows*cols;i++) ptr[i] = other.ptr[i];
}
short& operator [] (int n) {
return ptr[n];
}
void put(int row,int col,bool max_player) {
//假设坐标合理输入
if(ptr[row*cols+col]==0) {
ptr[row*cols+col] = max_player?1:-1;
this->max_player = !max_player;
}
}
void put_child(ChessBoard *child) {
child->next_borther = childs;
childs = child;
}
int where_is_void(int where[]) {
//查看now中空白位置,并返回数量n以及位置where = i*cols+j
int n=0;
for(int i=0;i<rows*cols;i++) {
if(ptr[i] == 0) where[n++] = i;
}
return n;
}
void show() {
//cout<<"++++"<<endl;
for(int i=0;i<rows;i++) {
for(int j=0;j<cols;j++) {
char c = '-';
if(ptr[i*cols+j]==1) c = 'o';
if(ptr[i*cols+j]==-1) c = 'x';
cout<<c;
}
cout<<endl;
}
cout<<"++++"<<endl;
}
int who_win() {
int sum = 0;
for(int i=0;i<rows;i++) {
sum = 0;
for(int j=0;j<cols;j++) sum+=ptr[i*cols+j];
if(sum==3) return 1;
if(sum==-3) return -1;
}
for(int i=0;i<cols;i++) {
sum = 0;
for(int j=0;j<rows;j++) sum+=ptr[i+cols*j];
if(sum==3) return 1;
if(sum==-3) return -1;
}
sum = 0;
for(int i=0;i<rows;i++)
sum +=ptr[i*cols+i];
if(sum==3) return 1;
if(sum==-3) return -1;
sum = 0;
for(int i=0,j=2;i<rows;i++,j--)
sum +=ptr[i*cols+j];
if(sum==3) return 1;
if(sum==-3) return -1;
return 0;//平局
}
int evaluate() {
//关键
if(who_win()==1) return MAX_INT;
else if(who_win()==-1) return MIN_INT;
return (how_win(1) - how_win(-1));
}
};
void creat_Tree(queue<ChessBoard*> &qu_chess,ChessBoard &now,int layer=4) {
//广度优先生成树
int size = now.rows*now.cols;
int where[size]; //row = where/(cols);col = where%(cols)
qu_chess.push(&now);
qu_chess.push(NULL); //第一层结束标志
while(!qu_chess.empty()) {
ChessBoard *live = qu_chess.front(); //取出一节点作为扩展节点
qu_chess.pop();
if(!live) {
layer--;
if(0==layer) break; //生成layer层后退出
qu_chess.push(NULL); //作为一层结束标志
live = qu_chess.front();
qu_chess.pop();
}
int n = live->where_is_void(where); //可放棋子位置与个数
for(int j=0;j<n;j++) {
ChessBoard *child = new ChessBoard();
(*child) = (*live);
child->put(where[j]/(child->cols),where[j]%(child->cols),(live->max_player));
child->father = live;
live->put_child(child);
qu_chess.push(child); //孩子待扩展
}
}
}
void dispose_tree(ChessBoard *node) {
//释放node的搜索树 (except node )
if(node->childs == NULL) return ;
else {
ChessBoard *next,*tmp = node->childs;
while(tmp) {
dispose_tree(tmp);
next = tmp->next_borther;
delete tmp;
tmp = next;
}
}
}
int minmax_recu(ChessBoard *node,int depth,bool max_player) {
//递归极大极小判断
if(depth==0 || node->childs==NULL) { //到达指定深度或者节点不可扩展
return node->evaluate();
}
if(max_player) { //此次操作为MAX
int bestval = MIN_INT;
ChessBoard *tmp = node->childs;
while(tmp) { //所有孩子取最大
tmp->value = minmax_recu(tmp,depth-1,false);
bestval = max<int>(bestval,tmp->value);
tmp = tmp->next_borther;
}
return bestval;
} else { //此次操作为MIN
int bestval = MAX_INT;
ChessBoard *tmp = node->childs;
while(tmp) { //所有孩子取最小
tmp->value = minmax_recu(tmp,depth-1,true);
bestval = min<int>(bestval,tmp->value);
tmp = tmp->next_borther;
}
return bestval;
}
}
void MAX_MIN_search(ChessBoard &now_node,int &row,int &col) {
//极大极小搜索
//给出初始局面,计算四步推算下一步走法(row,col)
queue<ChessBoard*> qu_chess;
//生成2层搜索树
creat_Tree(qu_chess,now_node,2);
//反向极大极小推理,得到目标步骤
now_node.value = minmax_recu(&now_node,2,now_node.max_player);
ChessBoard *tmp = now_node.childs->childs;
tmp = now_node.childs;
while(tmp && tmp->value!=now_node.value) {
tmp = tmp->next_borther;
}
for(int i=0;i<now_node.rows*now_node.cols;i++)
if(now_node[i]!=(*tmp)[i]) {
row = i/(now_node.cols);col = i%(now_node.cols);
}
//销毁搜索树
dispose_tree(&now_node);
}
int main() {
//这里只做了一步预测
//实际模拟可以实例化两个CHessBoard,分别作为对手
//各自都以自己为MAX来完成自行对弈
//其次,在搜索中若一定会出现平局或者最终根本赢不了时,
//这里给出的中间步骤无参考性。
ChessBoard p;
int next_row=0,next_col=0;
//设置初态
p.put(2,2,true);
p.put(0,2,false);
MAX_MIN_search(p,next_row,next_col);
p.put(next_row,next_col,true);
p.show();
return 0;
}关于单纯极大极小搜索的说明
由上可以看出,单纯的极大极小搜索需要在每一步判断时对问题进行所有可能性的枚举,并且依据对于搜索深度的要求,生成一个空间复杂度较高的树。每一步判断如此累加,将导致整个算法树的生成与搜索效率降低。
Alpha-Beta剪枝
在极大极小搜索生成博弈搜索树的时候,会生成规定深度内的所有节点,然后估值倒推。这样把生成与估值倒推分离,降低了效率。我们来介绍Alpha-Beta算法(以后简称α-β剪枝)。他的原理是把生成后继节点与倒退估值结合,减去无用分支,以此来提高效率。
借助极大极小搜索的特点---MAX节点对应A值,不会下降,MIN节点对应的B值不会上升。这里的A-B值分别指倒推时对应节点的值。
对于MAX来说,其某个后继节点MIN的B值小于该MAX或者更早的先辈节点的A值时,停止对该MIN节点的搜索。同理,当某个MAX节点的A值大于等于其先辈MIN节点的B值时,停止对该节点的搜索。由此,我们可以得到,A-B必须要求搜索树某一部分达到最深计算出一部分MAX的A值或者MIN的B值,随着搜索,不断改进A-B值。
剪枝规则总结
1. A剪枝:任何MIN的B小于任何他的先辈MAX的A时,停止该MIN以下的所有搜索,这个MIN的最终倒推值为当前的B值。(该B可能与真正的不同,但是没关系,不影响最终结果)
2. B剪枝:任何MAX的A大于或者等与他的先辈MIN的B时,停止该MAX节点以下的所有搜索,这个MAX的最终倒推值为当前的A值。
过程见下图解(标出真正搜索过的路径)
红色笔画出箭头的地方为搜索经过的地方,没有箭头的为被剪枝部分。
标注出的红色数字为该节点的A或者B值。
下图为另一图解(标出剪枝部分)
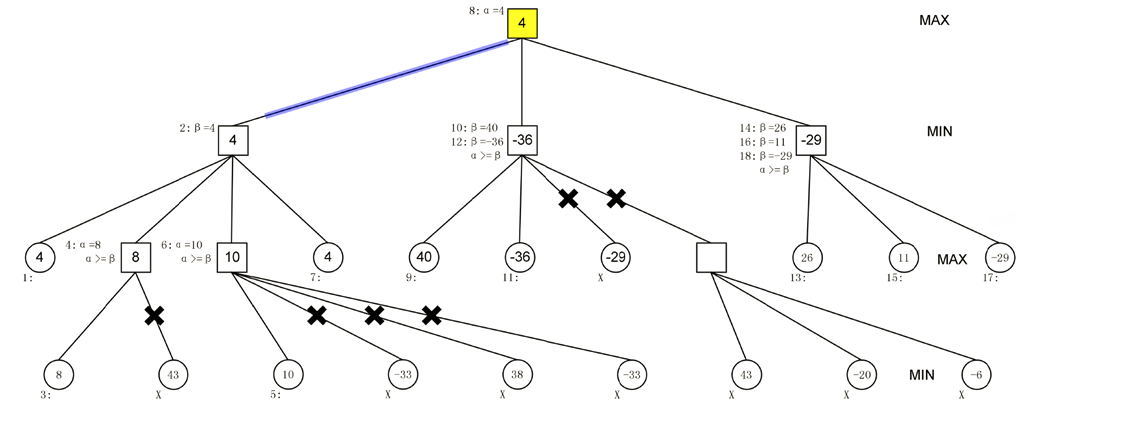
说明
A- 剪枝的效率与最先生成的A-B值与最终的倒推值有关,越相近,剪枝越提前并越快。
最佳情况下搜索深度为d的叶节点数相当于单纯MINMAX生成的深度为d/2的博弈树的节点数。有效分支系数为sqrt(b),而不是b,即假设某一步有4种情况,而用上A-B剪枝,情况变为2种。
























 3584
3584

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








