探索有交易成本的环境下期权Delta对冲频次与定价效果的关系

1.理论背景

金融机构在场外市场向客户卖出期权后会面临风险管理问题。如果出售的期权刚好与交易所内的期权相同，那么这家金融机构可以在交易所买入相同的期权来对冲其风险暴露。但是如果在场外卖出的期权比较特殊，这时通过在交易所内直接购买期权对冲卖出期权的风险会比较困难。

例如，某家金融机构以330,000元卖出了一份对应100,000股无息股票半年期的欧式看涨期权，执行价格K=50元，当前股票价格S_0=49元。假设无风险利率为5%，股票价格波动率sigma=20%，根据Black-Scholes定价模型：

 

数据带入计算可得期权价格约为287,445.20元，换算到期末294,721.91元。期权价格与机构售价之间的差额也就是机构赚取的风险之外的利润。

这时金融机构将面临着对冲风险的问题。如果股票在未来半年内涨到54元，对手方行权，(54-50)×100,000-294,721.91=105,278.09元；而如果选择直接在市场购入100,000股股票，如果股票价格半年后跌到45元，对手方不行权，(49-45)×100,000-294,721.91=105,278.09元，亏损10万元的风险令人不得不重视。

在根据BSM给期权定价的过程中涉及到了期权Delta的概念，也就是期权价格变动与其标的资产价格变动的比率。所以这时该金融机构只需要购买100,000×Δ股股票，让资产组合的整体Delta为0（也叫Delta中性），就能保证当股价发生微小波动时，资产总价值是不变的。可是由于期权Delta会随股票价格的变化而变化，这种投资组合的Delta中性状态只能在短时间维持，对冲策略需要不断做出调整，这种调整过程也叫再均衡。

对冲也是需要成本的，一方面是对冲操作本身的成本，以该金融机构卖出的看涨期权为例，当股票价格上涨时机构需要买入股票，当股票价格下跌时机构需要卖出股票，这里的差价以及买卖股票占用资金的利息都是对冲本身的成本。理论上调整越频繁，对冲效果也就越好，最终成本也就越趋近于BSM模型的定价——事实上BSM正是通过建立一个Delta中性的头寸，并论证该交易组合收益率为无风险收益率来为期权定价的。

另一方面是买卖股票的交易成本。如果机构可以每时每刻都在调整仓位，那么机构可以完全对冲掉风险，从而只赚取期权售价与BSM模型计算得到价格的差，这里也就是3万元，但现实中还存在买卖股票的交易成本，操作过于频繁会产生高昂的交易费用，最终对冲成本会超出期权定价，得不偿失。

如果没有手续费等交易成本，该金融机构可以通过频繁对冲操作来消除风险，赚取3万元的纯利润，可是在当下的环境中，交易手续费并非是一个可以忽略的参数，以此为背景讨论Delta对冲最佳频率问题也就具有了现实意义。

2.理想情况下对冲频率与对冲效果的关系

本文先研究没有交易费用的情况下，对冲频率的选择对于对冲效果的影响。这里使用Excel自动随机生成0.5年内5000个时间点（两两间隔6分钟，隔日股价不考虑跳空的情况）变化服从对数正态分布的股票价格，依次计算Delta，买卖股票费用，对冲成本，浮动盈亏，绘制时间变化折线图。

其中，Delta的计算方法为：

N( )为正态分布的累计概率函数，d1由BSM公式给出：

Amount_To_Buy计算公式：

浮动盈亏计算方法：

若St<=K:

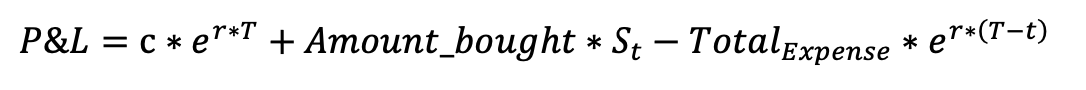
若St>k:

2.1.涉及参数

模拟的背景依然选取上文中金融机构，相关参数如下。

T_总时长	对冲频率	Δt_间隔时间	Δt_最小间隔	σ_波动率	n_标的单位	K_执行价格	S_0_期初价格	r_无风险收益率
0.500	\	0.0001	0.0001	0.2	100000	50	49	0.05

2.2.部分模拟过程

这里提供一些Excel表格公式截图：

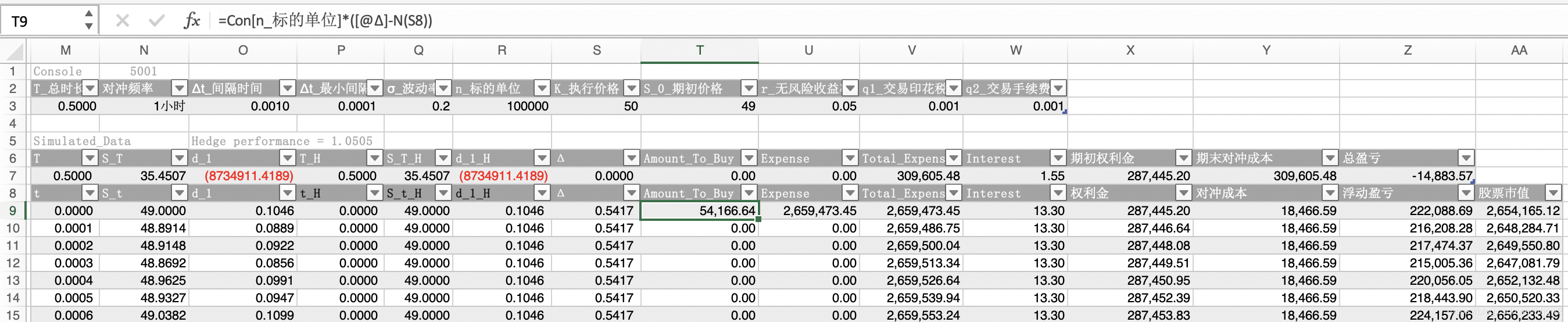
这里权利金也就是期权费，由BSM模型定价得出：

t	S_t	d_1	Δ	Amount_To_Buy	Expense	Total_Expense	Interest	权利金	对冲成本	浮动盈亏	股票市值
0.0000	49.0000	0.1046	0.5417	54,166.64	2,659,473.45	2,659,473.45	13.30	287,445.20	18,466.59	222,088.69	2,654,165.12
0.0001	48.8914	0.0889	0.5354	-624.37	-30,551.82	2,628,934.93	13.14	287,446.64	18,359.94	217,007.07	2,617,758.42
0.0002	48.9148	0.0922	0.5367	132.69	6,503.63	2,635,451.70	13.18	287,448.08	18,393.50	218,081.02	2,625,500.56
0.0003	48.8692