观前提醒:
笔试所有系列文章均是记录本人的笔试题思路与代码,从中得到的启发和从别人题解的学习到的地方,所以关于题目的解答,只是以本人能读懂为目标,如果大家觉得看不懂,那是正常的。如果对本文的某些知识有不同的观点,欢迎讨论。
题目链接:
第一题:乒乓球筐__牛客网
第二题:组队竞赛_牛客笔试题_牛客网
第三题:删除相邻数字的最大分数_牛客题霸_牛客网【重做】
---------------------------------------------------我是分割线---------------------------------------------------------------
---------------------------------------------------我是分割线---------------------------------------------------------------
---------------------------------------------------我是分割线---------------------------------------------------------------
---------------------------------------------------我是分割线---------------------------------------------------------------
---------------------------------------------------我是分割线---------------------------------------------------------------
第一题

思路:
一道特别简单的哈希表的应用,直接根据题意就可以了。题目的要求就是判断,B是不是A的子集就好。
代码:
#include <iostream>
#include <string>
#include <unordered_map>
using namespace std;
int main() {
string A, B;
while(cin>>A>>B)
{
unordered_map<char,int> hash;
bool flag=false;
for(auto& e:B)
{
hash[e]++;
}
for(int i=0;i<A.size();i++)
{
hash[A[i]]--;
}
for(auto& [a,b]:hash)
{
if(b > 0)
{
flag=true;
}
}
if(flag) cout<<"No"<<endl;
else cout<<"Yes"<<endl;
}
return 0;
}---------------------------------------------------我是分割线---------------------------------------------------------------
---------------------------------------------------我是分割线---------------------------------------------------------------
---------------------------------------------------我是分割线---------------------------------------------------------------
第二题

思路:
这还是一道比较简单的贪心题目,根据题意我们的要求是让总和最大,那我们可以让每个小组的中位数最大,既然想要中位数最大,但是我们取不到最大的值,那我们只能取第二大的值了,但是小组还有一个位置,但是这个位置上的数是没有的,所以我们可以选择当前最小的数字填上去,那我们的贪心策略不就出来了,每一组分配当前数组中最大值与次大值,最小值就好。
并且题目只是要求我们求出最大和,我们没有必要真从数组中挑选数字,我们直接找到中位数加起来就好了。
代码:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main() {
long long n=0;
cin>>n;
vector<long long> nums(n*3);
long long sum=0;
for(int i=0;i<n*3;i++)
{
int a=0;
cin>>a;
// cout<<a<<endl;
nums[i]=a;
}
sort(nums.begin(),nums.end());
int k=0,i=n*3-2;
while(k<i)
{
sum+=nums[i];
i-=2;
k++;
}
printf("%lld\n",sum);
return 0;
}---------------------------------------------------我是分割线---------------------------------------------------------------
---------------------------------------------------我是分割线---------------------------------------------------------------
---------------------------------------------------我是分割线---------------------------------------------------------------
第三题

思路:
这道题还是一道比较经典的dp问题,间隔取数字,我们如果只是对原数组讨论的话,其实不还做,因为我们想要找的和最大的情况,我们就必须判断每个元素有多少,并且要考虑元素本身数字大小带来的影响,所以方便讨论我们选择将数组的元素放入哈希表中。
观察哈希表我们的dp解法的思路不就有了吗?
我们可以看到下标就表示的是元素本身,这道题目就转化为了在一群有序数组中找到最大和,满足题目条件。
这种类型的题目是典型的打家劫舍题目。
根据状态表示我们可以直接开辟两个大小是原数组中最大值的dp表,具体含义如上。
至于状态转移方程,我们直接分类讨论就好了。
代码:
#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <unordered_map>
using namespace std;
int main() {
int n = 0;
cin >> n;
unordered_map<long long, int> hash;
long long M = 0;
long long x = 0;
for (int i = 0; i < n; i++) {
cin >> x;
M=max(M,x);
hash[x]++;
}
long long ret = 0;
vector<long long> dp(1e4+1, 0); //dp[i]表示选取i元素的时候,能得到的最多分。
vector<long long> fp(1e4+1, 0); //fp[i]表示不选取i元素的时候,能得到的最多分。
for (int i = 1; i <= M; i++) {
dp[i]=hash[i]*i+fp[i-1];
fp[i]=max(dp[i-1],fp[i-1]);
ret = max(ret, max(dp[i],fp[i]));
}
printf("%lld\n", ret);
return 0;
}










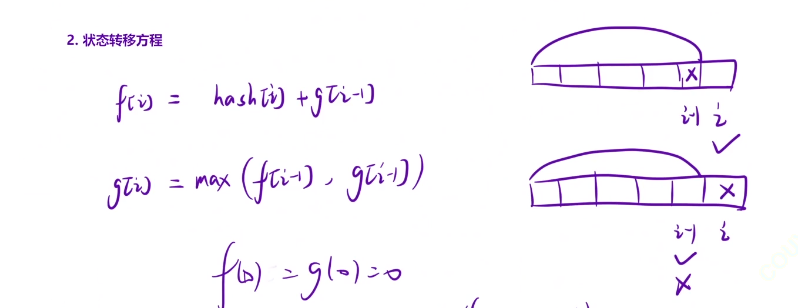


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








