【开关电源六】buck电路的输出纹波定量分析走一波？

👉个人主页： highman110
👉作者简介：一名硬件工程师，持续学习，不断记录，保持思考，输出干货内容

---

        在TI官网发现一篇关于降压开关电源的输出纹波定量分析，看完觉得挺不错的，于是大概整理翻译了一下分享出来。以往我们分析开关电源的一次纹波都是定性分析，知道输出电压纹波和电感纹波电流、输出滤波电容ESR等有关，今天我们用数学、用等式、用计算来定量进行分析，进一步佐证定性分析的结论。TI文档的链接如下，大家有兴趣可以看看原文，我的整理没有全文翻译，可能有遗漏。https://www.ti.com.cn/cn/lit/an/slva630a/slva630a.pdf

        如下图1为同步Buck电路基本拓扑，图2为电感电流、输出电流、电容电流关系图：

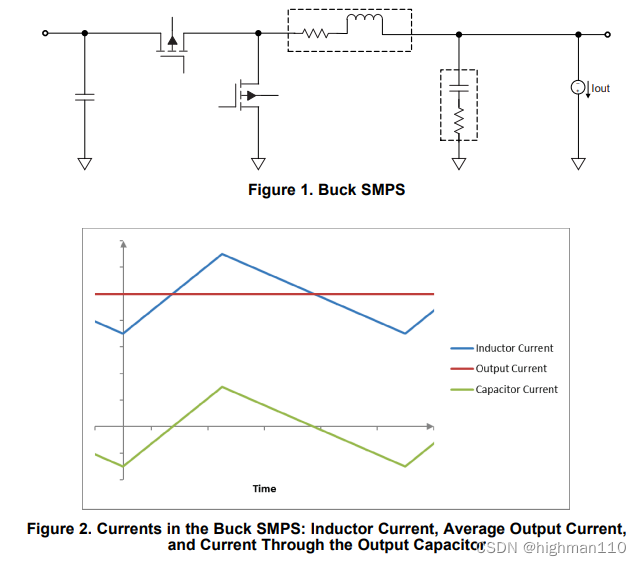
        根据基本电路定律基尔霍夫电流定律可以知道，buck电路的电感输出电流等于负载电流和流过滤波电容的电流之和。电感输出的纹波电流和滤波电容、负载无关，只和开关频率、占空比、输入输出电压有关。可以理解为流过电感的电流等于输出负载电流和流经电容的纹波电流之和。

        电感电流可以假设为一个理想的电流源，如下图：

        可得如下表达式：

----------1

        其中iripple(t)为流经电容的电流；

        从图2可以看出，纹波电流在MOS管导通和关断两个时间周期里是两断不同的表达式，且根据电感充电和放电阶段的能量是相等的，所以这个纹波电流的平均值是0：

-------------2

        已知纹波电流的峰峰值，即MOS管打开时，电感电流的变化量，这是可以通过电感欧姆定律算出来的：Ip2p=（Vin-Vo）*Ton /L。

        所以纹波电流的两段是可以用线性方程表示出来的（大家在坐标轴上选两个点自己算一下哈）：

-----------3

        电容上的电压等于理想电容C和等效串联电阻R上的电压之和（为简化计算，忽略等效串联电感）：

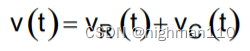-----------4

        将电流代入上式：

-----------5

        假设电容上的初始电压为0，针对MOS管导通阶段，将公式3代入公式5得：

----------6

        可以看到，上面的方程是个关于t的一元二次方程，它的波形是一个开口向上的抛物线，因为t2的系数大于0（大家不记得一元二次方程的波形了可再百度温习一下中学数学知识）。

        于是对上面的函数求导，导数等于0时，Vi（t）将到达最小值。

----------7

        上式可以解出：

----------8

        可以看到Vi（t）将在MOS管导通时间进行到一半还差一个RC常数时达到最小值，由于时间不会小于0，所以tmin ≥ 0。

        将式子8代入6，可得Vi（t）最小值：

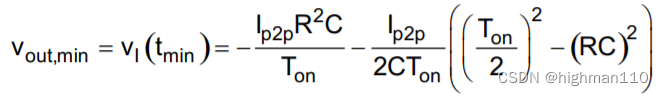----------9

        同样的，针对第二段纹波电流函数，MOS管关断时段，将3代入5，得：

----------10

        这是一个开口向下的抛物线，同样对上面的函数求导，可以得到函数最大值时的t值：

----------11

        同样的这个时间不会小于0，将11代入10，可得：

----------12

        至此，我们得到了MOS管打开和关闭两个时段的输出电压纹波的表达函数，同时得到了最大值和最小值。

        所以输出纹波的峰峰值为：

----------13

        下面分三种情况分析：

1、RC常数很小时：

----------14

        此时纹波峰峰值为：

----------15

        开关时间和占空比与开关频率之间的关系如下：

----------16

        可计算得出峰峰值的表达式为：

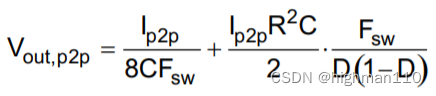----------17

        通常情况下，我们把理想电容和ESR对纹波的作用分开来考虑。仅考虑电容部分，将等效串联电阻设置为0，R=0，则代入上式给出了一个熟悉的表达式VC=Ip2p/（8CFsw）。如果输出电路上只有电阻器，则电阻部分为VR=Ip2pR。

                等式17可以写成：

----------18

        将等式18与等式17进行比较，可以发现，总输出纹波不能用简单的用电阻和电容产生的纹波和来表示；其他因素，如占空比、开关频率以及电阻器和电容器的值也起作用。

2、RC常数很大时：

        使得抛物线函数的顶底点在0时刻左侧，显然，时间不会小于0，所以t=0时，代入公式6和10，即为纹波电压的最大和最小值，

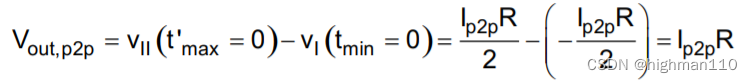----------19

        上式表明，当RC时间常数比较大时，纹波最大值由电阻R决定，和电容值无关。

  

3、RC常数在中间：

        估算：为了快速计算，通常假设一个输出电压纹波的简单模型。通用的模型有线性模型和RMS模型。

        线性模型，总输出纹波等于电容和电阻分别引起的电压波动的线性叠加：

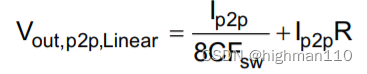------------24

        RMS模型，总输出纹波等于电容和电阻分别引起的电压波动的RMS平均值

------------25

        线性和均方根近似值没有直接的占空比相关性，如下图所示。

        两种近似值都有误差。线性近似可能有近60%的误差；在占空比接近0.5时，RMS近似值的误差为15%。

        这两种估算都不能从给出的分析模型中推导出来。他们是手动计算可接受的近似值，在工程上我们经常用线性模型的公式进行输出纹波的计算评估，这个估算值是偏大的，但在工程上估算偏大就表示设计的余量更大，一般不会有问题，成本上可能略有增加。