文章目录
| 题型 | |
|---|---|
| 函数 | 1. 函数的运算与性质:有界性、单调性及其奇偶性的判定 2. 复合函数 |
| 极限 | 1. 无穷小量阶的比较 2. 求极限 3. 极限的概念、性质及存在法则 |
| 函数连续性 | 1. 函数连续性及其间断点类型 2. 连续函数性质的证明题 |
一. 知识点:函数、极限、连续
1. 函数
函数分类
基本初等函数
反函数:与直线关于y=x对称。
参数式函数
复合函数
幂函数图像
函数性质
函数的单调、周期、有界。
2. 极限
定义
数列极限:定义ing
函数极限:
- 左右极限
- 极限与连续性
极限存在
极限存在:对于数列,2n和2n-1项极限相同;对于函数,左极限=右极限。
3. 函数的连续性与间断
连续
一点连续: x 0 x_0 x0的邻域有定义,且此处的函数值=极限值
闭区间连续:定义内都连续,且边界点(右边界点)左连续( x 0 − x_0^- x0−)与(左边界点)右连续( x 0 + x_0^+ x0+)
间断点的类型
第一类间断点:
- 可去间断点:左右极限存在且相等,但此处无定义
- 跳跃间断点:左右极限存在但不相等
第二类间断点:
连续函数的性质

二. 求极限的方法
1. 常见等价无穷小

x m + x k − x m ( k > m > 0 ) {x^m + x^k} {-} {x^m}(k>m>0) xm+xk−xm(k>m>0)
2. 重要极限
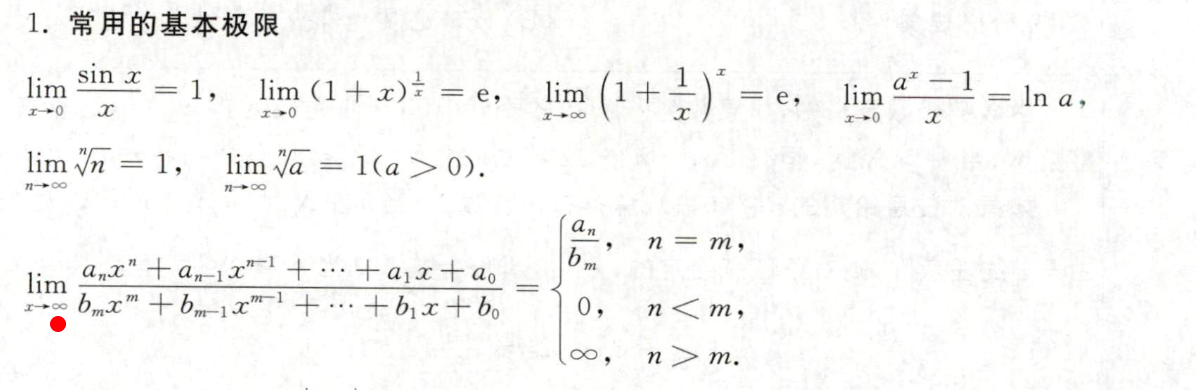

3. 极限的有理运算法则

4. 洛必达


5. 泰勒公式
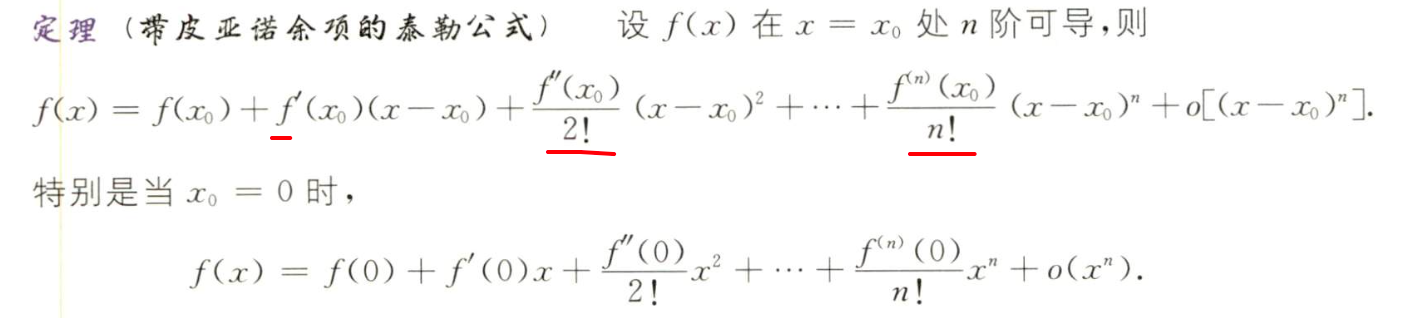
常见泰勒公式
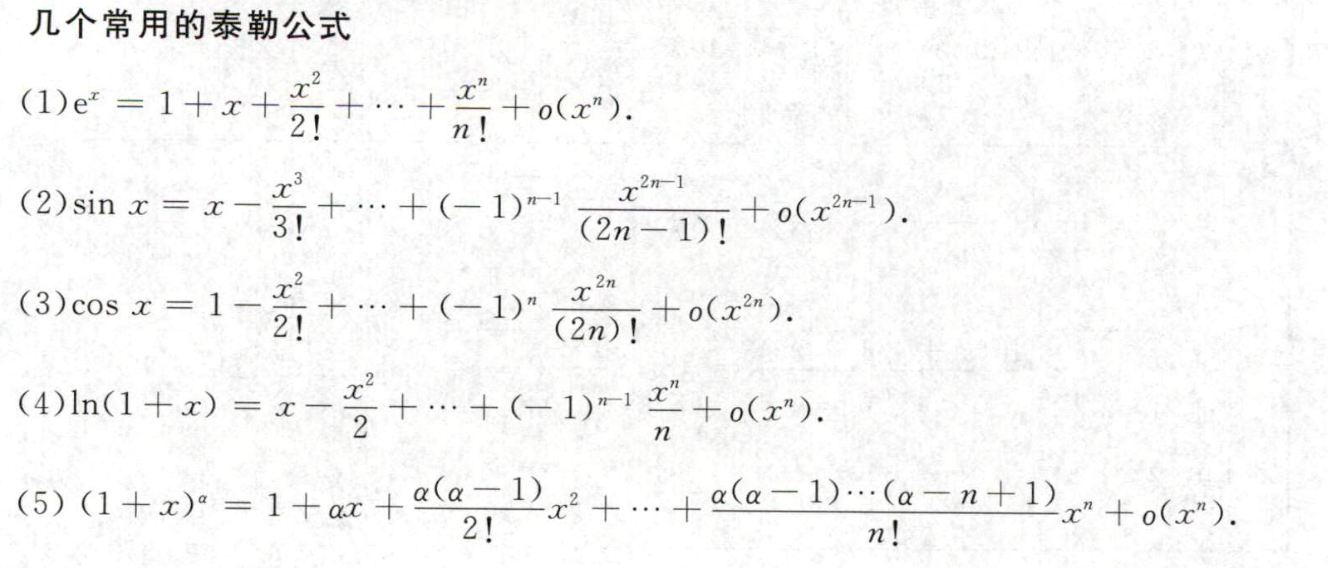



























 1472
1472

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










