动态规划之斜率优化专题

最新推荐文章于 2022-11-29 20:33:49 发布

剑锋OI

最新推荐文章于 2022-11-29 20:33:49 发布

阅读量723

点赞数 1

分类专栏：算法总结动态规划问题动态规划斜率优化文章标签：动态规划

本文链接：https://blog.csdn.net/hjf1201/article/details/78779660

版权

算法总结动态规划问题同时被 2 个专栏收录

12 篇文章 1 订阅

订阅专栏

动态规划斜率优化

1 篇文章 0 订阅

订阅专栏

“DP的斜率优化——对不必要的状态量进行抛弃，对不优的状态量进行搁置，使得在常数时间内找到最优解成为可能。斜率优化依靠的是数形结合的思想，通过将每个阶段和状态的答案反映在坐标系上寻找解答的单调性，来在一个单调的答案（下标）队列中O（1）得到最优解。”

”一些试题中繁杂的代数关系身后往往隐藏着丰富的几何背景，而借助背景图形的性质，可以使那些原本复杂的数量关系和抽象的概念，显得直观，从而找到设计算法的捷径。”—— 周源《浅谈数形结合思想在信息学竞赛中的应用》

斜率优化的核心即为数形结合，具体来说，就是以DP方程为基础，通过变形来使得原方程形如一个函数解析式，再通过建立坐标系的方式，将每一个DP方程代表的状态表示在坐标系中，在确定“斜率”单调性的前提下，进行形如单调队列操作的舍解和维护操作。

【HDU3045】Picnic Cows

【在线测试提交传送门】

【解题思路】

首先，审题。可以打乱序列顺序，又知道代价为组内每个元素与最小值差之和，故想到贪心，先将序列排序（用STL sort）。
先从最简单的DP方程想起：
容易想到：

f[i] = min( f[j] + (a[j + 1 -&gt; i] - Min k) ) （0 &le; j &lt; i） 
– –> f[i] = min( f[j] + sum[i] - sum[j] - a[j + 1] * ( i - j ) )

Min k 代表序列 j + 1 ->i内的最小值，排序后可以简化为a[j+1]。提取相似项合并成前缀和sum。这个方程的思路就是枚举 j 不断地计算状态值更新答案。但是数据规模达到了40000，这种以O（n^2）为绝对上界方法明显行不通。所以接下来我们要引入“斜率”来优化。

首先要对方程进行变形：

f[i] = f[j] + sum[i] - sum[j] - a[j + 1] * ( i - j ) 
– –> f[i] = (f[j] - sum[j] + a[j + 1] * j) - i * a[j + 1] + sum[i]

（此步将只由i决定的量与只由j决定的量分开）
由于 sum[i] 在当前枚举到i的状态下是一个不变量，所以在分析时可以忽略（因为对决策优不优没有影响）（当然写的时候肯定不能忽略）

令 i = k 
 a[j + 1] = x 
 f[j] - sum[j] + a[j + 1] * j = y 
 f[i] = b 
原方程变为 – –> b = y - k * x 
移项 – –> y = k * x + b

是不是很眼熟？没错，这就是直线的解析式。观察这个式子，我们可以发现，当我们吧许许多多的答案放在坐标系上构成点集，且枚举到 i 时，过每一个点的斜率是一样的！！很抽象？看图
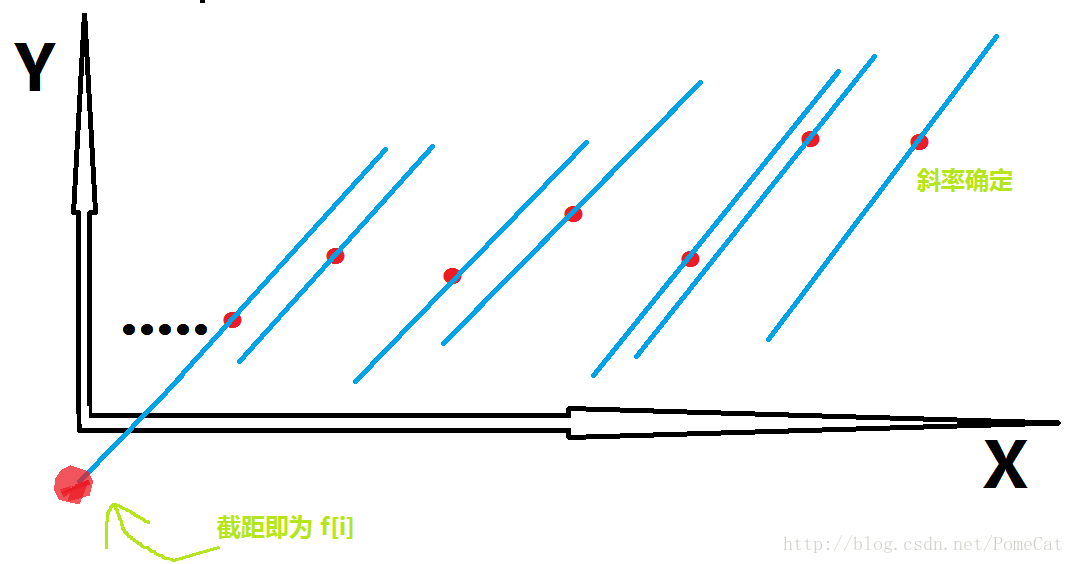
此处输入图片的描述
可以看出，我们要求的f[i]就是截距，明显，延长最右边的直线交于坐标轴可得最小值。难道只要每次提取最靠近 i 的状态就行了嘛？现实没有那么美好。

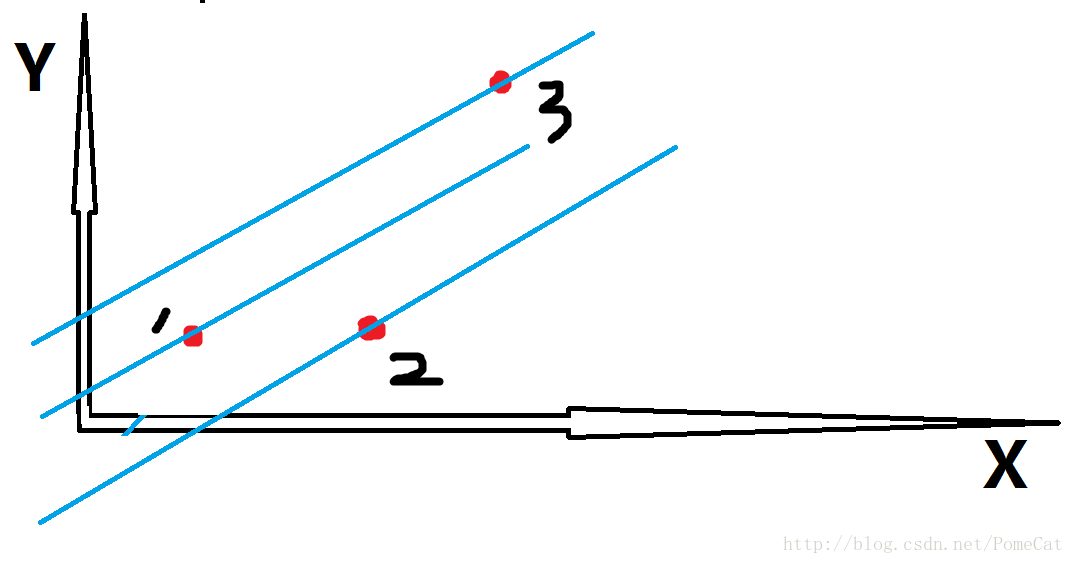
像这样的情况，过2直线的截距明显比过3直线的截距要小，意味着更优（在找求解最小值问题时），这种情况下我们之前的猜想便行不通。

那怎么办呢？这时就要用到斜率优化的核心思想——维护凸包。
何为凸包？
参考凸包相关知识

其实我们要维护的凸包与这个凸包并无关系，只是在图中长得像罢了。
那为什么要维护凸包呢？
还要看图：
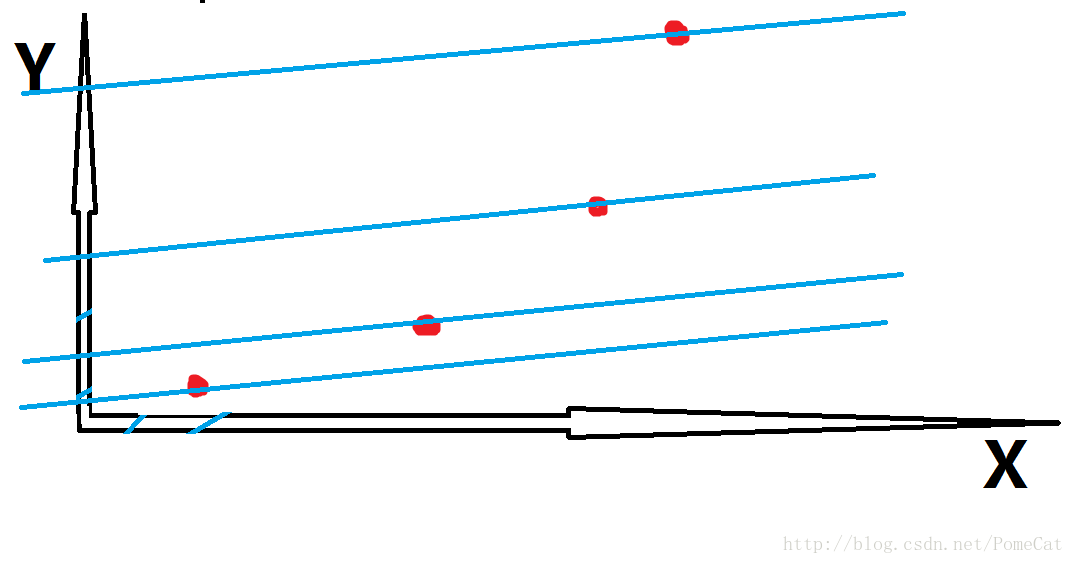
此处输入图片的描述
这就是一个下凸包，由图可见，最前面的那个点的截距最小，也诠释了维护凸包的真正含义（想一想优先队列，是不是队首最优？）。那还是有人会提出疑问，为什么非要维护这样的凸包呢？答案就是，f[i]明显是递增的（相比于f[j] 加上一个代价），所以会在图中自然而然地显现出 Y 随着 X增加而增加的情况，呈现出凸包的模样。

可能这个过程比较晦涩难懂，没懂的同学可以多看几遍。

现在我们回到对数的分析

现在假设我们正在枚举 j 来更新答案，有一个数 k， j < k < i
再来假设 k 比 j 优（之所以要假设正是要推出具体情况方便舍解）

则有

f[k] + sum[i] - sum[k] - a[k + 1] * (i - k) <= 
 f[j] + sum[i] - sum[j] - a[j + 1] * (i - j) (k > j)

移项消项得

f[k] - sum[k] + a[k+ 1] * k - (f[j] - sum[j] + a[j + 1] * j) <= 
 i * (a[k + 1] - a[j+ 1])

将只与 i 有关的元素留下，剩下的除过去，得到

f[k] - sum[k] + a[k+ 1] * k - (f[j] - sum[j] + a[j + 1] * j) / 
 a[k + 1] - a[j + 1] <= i 
（这里注意判断除数是否为负， 要变号，当然这里排序过后对于 k > j a[k] 肯定大于 a[j]）

这个式子什么意思呢？我用人类的语言解释一下。
设 Xi = a[i], Yi = f[i] - sum[i] + a[i + 1] * i
那么原式即为如下形式：
(Yk - Yj) / (Xk - Xj) <= i

意思就是当有k 和 j 满足 j < k 的前提下满足此不等式
则证明 j 没有 k 优

而这个式子的左边数学意义是斜率，而右边是一个递增的变量，所以递增的 i 会淘汰队列里的元素，而为了高效的淘汰，我们会（在这道题里）选用斜率递增的单调队列，也就是上凸包。（再看看前面的图，是不是斜率在递增）

我们还可以从另一个角度理解维护上凸包的理由

仔细观察下面的图：

一开始，1 号点的截距比2号点更优
此处输入图片的描述

随着斜率的变化，两个点的截距变得一样了

然后，斜率接着变化，1号点开始没有2号点优了，所以要舍弃

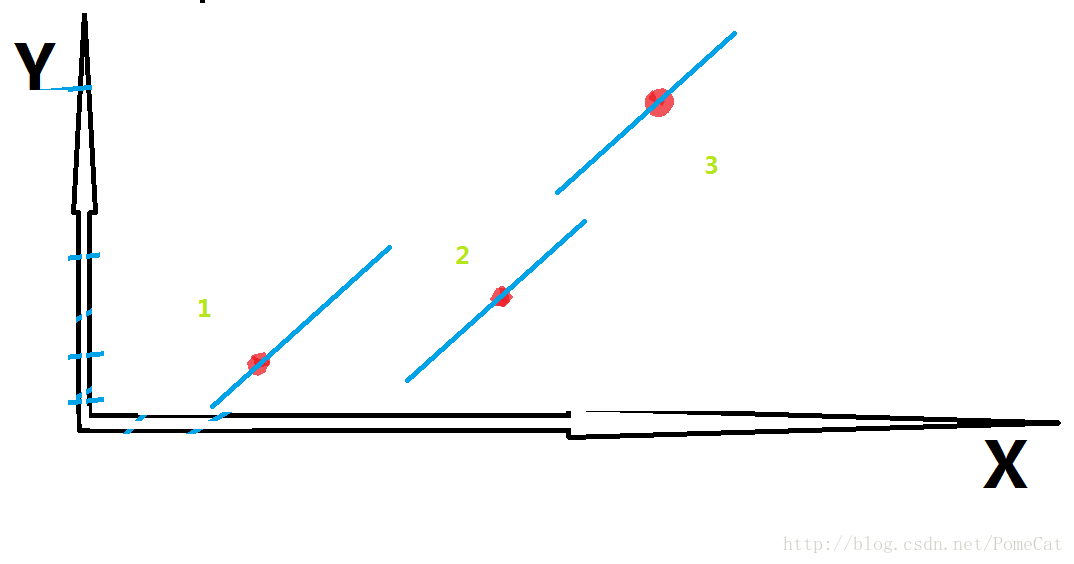
此处输入图片的描述
后面的过程，3号点会渐渐超过2号点，并淘汰掉2号点

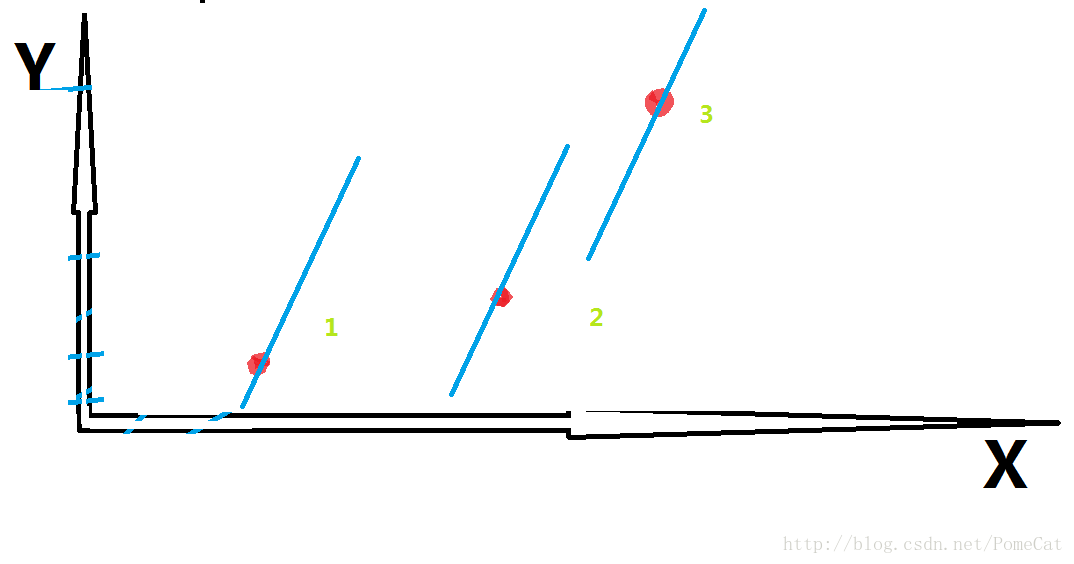
分析整个过程，最优点依次是 1 -> 2 -> 3，满足单调的要求

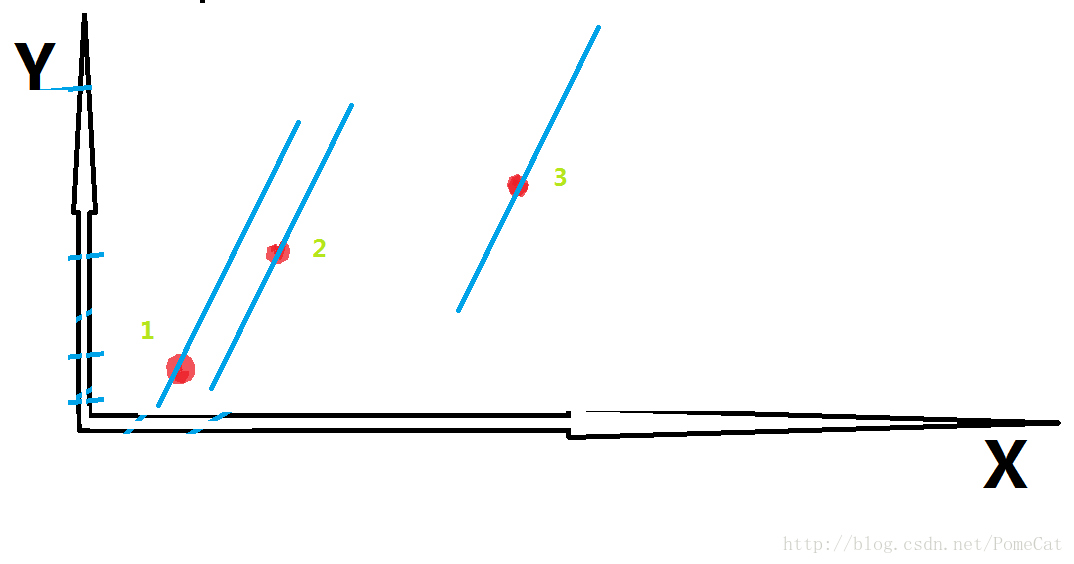
但是如果是一个上凸包会怎样呢？

这里只给出最终图（有兴趣的同学可以自己推一推），可以预见的是，在1赶超2前，3先赶超了2就破坏了顺序，因此不行
此处输入图片的描述
思路大概是清晰了，现在只剩下代码实现方面的问题了

下面就看看单调队列的操作

先将推出的X, Y用函数表示方便计算：
X：

dnt X( int i, int j )
{
    return a[j + 1] - a[i + 1];
}

（dnt 是 typedef 的 long long）

Y：

dnt Y( int i, int j )
{
    return f[j] - sum[j] + j * a[j + 1] - (f[i] - sum[i] + i * a[i + 1]);
}

处理队首：

for(; h + 1 < t && Y(Q[h + 1], Q[h + 2]) <= i * X(Q[h + 1], Q[h + 2]); h++);

从队尾维护单调性：
（这里是一个下凸包所以两点之间的斜率要递增，即斜率（1， 2） < 斜率（2， 3）, 前一个斜率比后一个小）

for(; h + 1 < t && Y(Q[t - 1], Q[t]) * X(Q[t], cur) >= X(Q[t - 1], Q[t]) * Y(Q[t], cur); t--);

（注意，要把除法写成乘的形式，不然精度可能会出问题）

斜率优化部分已经完结（说起来挺复杂其实代码很短），接下来就放出AC代码：

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;

typedef long long dnt;

int n, T, Q[405005];
dnt sum[405005], f[405005], a[405005];

dnt Y( int i, int j )
{
    return f[j] - sum[j] + j * a[j + 1] - (f[i] - sum[i] + i * a[i + 1]);
}

dnt X( int i, int j )
{
    return a[j + 1] - a[i + 1];
}

dnt DP( int i, int j )
{
    return f[j] + (sum[i] - sum[j]) - (i - j) * a[j + 1];
}

inline dnt R()
{
    static char ch;
    register dnt res, T = 1;
    while( ( ch = getchar() ) < '0'  || ch > '9' )if( ch == '-' )T = -1; 
        res = ch - 48;
    while( ( ch = getchar() ) <= '9' && ch >= '0')
        res = res * 10 + ch - 48;
    return res*T;
}

int main()
{
    sum[0] = 0;
    while(~scanf( "%d%d", &n, &T ))
    {
        a[0] = 0, f[0] = 0;
        for(int i = 1; i <= n; i++)
            scanf( "%lld", &a[i] );
        sort(a + 1, a + n + 1);
        for(int i = 1; i <= n; i++)
            sum[i] = sum[i - 1] + a[i];
        int h = 0, t = 0;
        Q[++t] = 0;
        for(int i = 1; i <= n; i++)
        {
            int cur = i - T + 1;
            for(; h + 1 < t && Y(Q[h + 1], Q[h + 2]) <= i * X(Q[h + 1], Q[h + 2]); h++);
            f[i] = DP(i, Q[h + 1]);
            if(cur < T) continue;
            for(; h + 1 < t && Y(Q[t - 1], Q[t]) * X(Q[t], cur) >= X(Q[t - 1], Q[t]) * Y(Q[t], cur); t--);
            Q[++t] = cur;
        }
        printf( "%lld\n", f[n] );
    }   
    return 0;
}

【CodeForces311B】Cats Transport

【在线测试提交传送门】

【问题描述】

  ssoi是一个大农场主，他养了m只猫，聘请了p个饲养员。沿着农场的道路有n座山，从左到右依次编号为1到n。第i座山和第i-1座山的距离是d[i]，饲养员都在第1座山。
  一天，小猫们都出去游玩，第i只猫游玩第h[i]座山，在t[i]时刻游玩结束，并在第h[i]座山等待饲养员去接它，所有猫都必须接回家。饲养员从第1座山出发走到第n座山，到达一座山时，将山上的猫接走，饲养员不会等待一只猫游玩结束，他只会接走正在等待的猫。饲养员的行走速度是1，他们非常有力，每次可以接走任意多只猫。
  例如，有两座山，d[2]=1，一只猫在第2座山（h[1]=2）,在时间3游玩结束，如果饲养员离开在时间2或者时间3离开第1座山，他能接走这只猫，因为饲养员不需要等待这只猫，但是如果他在时间1离开第1座山，他不能接走这只猫。
  请安排饲养员的出发时间，使得所有猫的等待的时间总和最小。

【输入格式】

第一行，3个整数n,m,p (2≤ n≤ 10^5, 1 ≤ m≤ 10^5, 1 ≤ p≤ 100)；
第二行，n-1个正整数d2,d3,...,dn (1≤ di＜10^4)；
接下来m行，每行两个整数hi和ti。(1≤ hi≤ n,0≤ ti≤ 10^9)。

【输出格式】

输出共一行，一个整数，表示所有猫的最小等待时间。

【输入样例】

【输出样例】

【解题思路】

  可以发现，每只猫的信息都可以浓缩为一个值：a[i]=t[i]-d[i]，即想要恰好接上这只猫，管理员的出发时间。那么，这只猫的等待时间即为管理员出发时间与这个值的差。 
 对a数组进行排序，这样每个管理员接走的猫一定是连续的一段。 
 求a[]的前缀和s[]。 
dp[i][j]表示前i个管理员接走前j只猫的最少总等待时间。 
 那么朴素的状态转移方程即为dp[i][j]=max{dp[i-1][k]+a[j]-a[k+1]+a[j]-a[k+2]+…+a[j]-a[j-1]}。 
 上式可化简为dp[i-1][k]+a[j]*(j-k)-(s[j]-s[k])。 
 那么朴素算法的时间复杂度为O(pm^2)。 
 因为有a[j]*k这一项，j和k无法完全分离，考虑斜率优化。 
 对于k2>k1，k2比k1优的充要条件是 ：
dp[i-1][k2]+a[j] * (j-k2)-(s[j]-s[k2])≤dp[i-1][k1]+a[j] * (j-k1)-(s[j]-s[k1]) 
记g(k)=dp[i-1][k]+s[k] 
化简得(g(k2)-g(k1))/(k2-k1)≤a[j]。 
 于是维护k递增、相邻两点斜率也递增，且所有斜率都大于a[j]的单调队列，则任意相邻两点都是左边优于右边，所以队首即为最优解。 
 维护的时候，因为a[j]单调不减，所以随着j增大，会出现队首两元素的斜率≤a[j]，也就是que[hd+1]优于que[hd]，这样弹出队首。 
 另外，插入新的j可能使尾部不满足斜率递增。也就是k(que[tl-1],que[tl])≤k(que[tl],j)。（分别记为k1，k2）那么对于以后出现的任何一个j’，如果k1大于a[j’]，那么que[tl-1]优于que[tl]。如果k1≤a[j’]，那么k2≤a[j’]，那么j优于que[tl]。所以que[tl]永远不是最优决策，弹出。 
 时间复杂度优化为O(pm)。 
 注意边界条件。

#include <bits/stdc++.h>
using namespace std;
const long long oo=1000000000233333;
int i,que[100010];
long long len[100010],a[100010],s[100010],dp[110][100010];
long long g(int k)
{
    return dp[i-1][k]+s[k];
}
int main()
{
    int j,k,m,n,p,q,x,y,z,hd,tl;
    scanf("%d%d%d",&n,&m,&p);
    for (i=2;i<=n;i++)
    {
        scanf("%d",&x);
        len[i]=len[i-1]+x;
    }
    for (i=1;i<=m;i++)
    {
        scanf("%d%d",&x,&y);
        a[i]=y-len[x];
    }
    sort(a+1,a+m+1);
    for (i=1;i<=m;i++)
      s[i]=s[i-1]+a[i];
    for (i=1;i<=m;i++)
      dp[0][i]=oo;
    for (i=1;i<=p;i++)
    {
        hd=1;
        tl=0;
        for (j=0;j<=m;j++)
        {
            while (hd<tl&&
              g(que[hd+1])-g(que[hd])<=
              a[j]*(que[hd+1]-que[hd]))
                hd++;
            dp[i][j]=g(que[hd])+a[j]*(j-que[hd])-s[j];
            while (hd<tl&&
              (g(j)-g(que[tl]))*
              (que[tl]-que[tl-1])<=
              (g(que[tl])-g(que[tl-1]))*
              (j-que[tl]))
                tl--;
            que[++tl]=j;
        }
    }
    printf("%lld\n",dp[p][m]);
}

剑锋OI

关注

1
点赞
踩
2

收藏

觉得还不错? 一键收藏
2
评论
动态规划之斜率优化专题

动态规划之斜率优化专题“DP的斜率优化——对不必要的状态量进行抛弃，对不优的状态量进行搁置，使得在常数时间内找到最优解成为可能。斜率优化依靠的是数形结合的思想，通过将每个阶段和状态的答案反映在坐标系上寻找解答的单调性，来在一个单调的答案（下标）队列中O（1）得到最优解。””一些试题中繁杂的代数关系身后往往隐藏着丰富的几何背景，而借助背景图形的性质，可以使那些原本复杂的数量关系和抽象的概念，显得直观，
复制链接

扫一扫