原文地址:http://blog.csdn.net/hjimce/article/details/49095371
作者:hjimce
一、相关理论
RNN(Recurrent Neural Networks)中文名又称之为:循环神经网络(原来还有一个递归神经网络,也叫RNN,搞得我有点混了,菜鸟刚入门,对不上号)。在计算机视觉里面用的比较少,我目前看过很多篇计算机视觉领域的相关深度学习的文章,除了OCR、图片标注、理解问答等这些会把CNN和RNN结合起来,其它的很少见到。RNN主要用于序列问题,如自然语言、语音音频等领域,相比于CNN来说,简单很多,CNN包含:卷积层、池化层、全连接层、特征图等概念,RNN基本上就仅仅只是三个公式就可以搞定了,因此对于RNN我们只需要知道三个公式就可以理解RNN了。说实话,一开是听到循环神经网络这个名子,感觉好难的样子,因为曾经刚开始学CNN的时候,也有很多不懂的地方。还是不啰嗦了,……开始前,我们先回顾一下,简单的MLP三层神经网络模型:
简单MLP模型
上面那个图是最简单的浅层网络模型了,x为输入,s为隐藏层神经元,o为输出层神经元。然后U、V就是我们要学习的参数了。上面的图很简单,每层神经元的个数就只有一个,我们可以得到如下公式:
(1)隐藏层神经元的激活值为:
s=f(u*x+b1)
(2)然后输出层的激活值为:
o=f(v*s+b2)
这就是最简单的三层神经网络模型的计算公式了,如果对上面的公式,还不熟悉,建议还是看看神经网络的书,打好基础先。而其实RNN网络结构图,仅仅是在上面的模型上,加了一条连接线而已,RNN结构图:
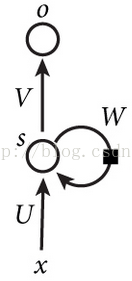
RNN结构图
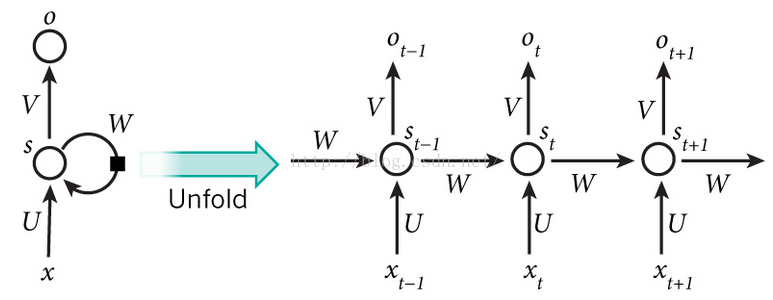
看到结构图,是不是觉得RNN网络好像很简单的样子,至少没有像CNN过程那么长。从上面的结构图看,RNN网络基础结构,就只有一个输入层、隐藏层、输出层,看起来好像跟传统浅层神经网络模型差不多(只包含输出层、隐藏层、输出层),唯一的区别是:上面隐藏层多了一天连接线,像圆圈一样的东东,而那条线就是所谓的循环递归,同时那个圈圈连接线也多了个一个参数W。还是先看一下RNN的展开图,比较容易理解:
我们直接看,上面展开图中,Ot的计算流程,看到隐藏层神经元st的输入包含了两个:来时xt的输入、来自st-1的输入。于是RNN,t时刻的计算公式如下:
(1)t时刻,隐藏层神经元的激活值为:
st=f(u*xt+w*st-1+b1)
(2)t时刻,输出层的激活值为:
ot=f(v*st+b2)
是不是感觉上面的公式,跟一开始给出的MLP,公式上就差那么一点点。仅仅只是上面的st计算的时候,在函数f变量计算的时候,多个一个w*s t-1。二、源码实现
下面结合代码,了解代码层面的RNN实现:
# -*- coding: utf-8 -*-
"""
Created on Thu Oct 08 17:36:23 2015
@author: Administrator
"""
import numpy as np
import codecs
data = open('text.txt', 'r').read() #读取txt一整个文件的内容为字符串str类型
chars = list(set(data))#去除重复的字符
print chars
#打印源文件中包含的字符个数、去重后字符个数
data_size, vocab_size = len(data), len(chars)
print 'data has %d characters, %d unique.' % (data_size, vocab_size)
#创建字符的索引表
char_to_ix = { ch:i for i,ch in enumerate(chars) }
ix_to_char = { i:ch for i,ch in enumerate(chars) }
print char_to_ix
hidden_size = 100 # 隐藏层神经元个数
seq_length = 20 #
learning_rate = 1e-1#学习率
#网络模型
Wxh = np.random.randn(hidden_size, vocab_size)*0.01 # 输入层到隐藏层
Whh = np.random.randn(hidden_size, hidden_size)*0.01 # 隐藏层与隐藏层
Why = np.random.randn(vocab_size, hidden_size)*0.01 # 隐藏层到输出层,输出层预测的是每个字符的概率
bh = np.zeros((hidden_size, 1)) #隐藏层偏置项
by = np.zeros((vocab_size, 1)) #输出层偏置项
#inputs t时刻序列,也就是相当于输入
#targets t+1时刻序列,也就是相当于输出
#hprev t-1时刻的隐藏层神经元激活值
def lossFun(inputs, targets, hprev):
xs, hs, ys, ps = {}, {}, {}, {}
hs[-1] = np.copy(hprev)
loss = 0
#前向传导
for t in xrange(len(inputs)):
xs[t] = np.zeros((vocab_size,1)) #把输入编码成0、1格式,在input中,为0代表此字符未激活
xs[t][inputs[t]] = 1
hs[t] = np.tanh(np.dot(Wxh, xs[t]) + np.dot(Whh, hs[t-1]) + bh) # RNN的隐藏层神经元激活值计算
ys[t] = np.dot(Why, hs[t]) + by # RNN的输出
ps[t] = np.exp(ys[t]) / np.sum(np.exp(ys[t])) # 概率归一化
loss += -np.log(ps[t][targets[t],0]) # softmax 损失函数
#反向传播
dWxh, dWhh, dWhy = np.zeros_like(Wxh), np.zeros_like(Whh), np.zeros_like(Why)
dbh, dby = np.zeros_like(bh), np.zeros_like(by)
dhnext = np.zeros_like(hs[0])
for t in reversed(xrange(len(inputs))):
dy = np.copy(ps[t])
dy[targets[t]] -= 1 # backprop into y
dWhy += np.dot(dy, hs[t].T)
dby += dy
dh = np.dot(Why.T, dy) + dhnext # backprop into h
dhraw = (1 - hs[t] * hs[t]) * dh # backprop through tanh nonlinearity
dbh += dhraw
dWxh += np.dot(dhraw, xs[t].T)
dWhh += np.dot(dhraw, hs[t-1].T)
dhnext = np.dot(Whh.T, dhraw)
for dparam in [dWxh, dWhh, dWhy, dbh, dby]:
np.clip(dparam, -5, 5, out=dparam) # clip to mitigate exploding gradients
return loss, dWxh, dWhh, dWhy, dbh, dby, hs[len(inputs)-1]
#预测函数,用于验证,给定seed_ix为t=0时刻的字符索引,生成预测后面的n个字符
def sample(h, seed_ix, n):
x = np.zeros((vocab_size, 1))
x[seed_ix] = 1
ixes = []
for t in xrange(n):
h = np.tanh(np.dot(Wxh, x) + np.dot(Whh, h) + bh)#h是递归更新的
y = np.dot(Why, h) + by
p = np.exp(y) / np.sum(np.exp(y))
ix = np.random.choice(range(vocab_size), p=p.ravel())#根据概率大小挑选
x = np.zeros((vocab_size, 1))#更新输入向量
x[ix] = 1
ixes.append(ix)#保存序列索引
return ixes
n, p = 0, 0
mWxh, mWhh, mWhy = np.zeros_like(Wxh), np.zeros_like(Whh), np.zeros_like(Why)
mbh, mby = np.zeros_like(bh), np.zeros_like(by) # memory variables for Adagrad
smooth_loss = -np.log(1.0/vocab_size)*seq_length # loss at iteration 0
while n<20000:
#n表示迭代网络迭代训练次数。当输入是t=0时刻时,它前一时刻的隐藏层神经元的激活值我们设置为0
if p+seq_length+1 >= len(data) or n == 0:
hprev = np.zeros((hidden_size,1)) #
p = 0 # go from start of data
#输入与输出
inputs = [char_to_ix[ch] for ch in data[p:p+seq_length]]
targets = [char_to_ix[ch] for ch in data[p+1:p+seq_length+1]]
#当迭代了1000次,
if n % 1000 == 0:
sample_ix = sample(hprev, inputs[0], 200)
txt = ''.join(ix_to_char[ix] for ix in sample_ix)
print '----\n %s \n----' % (txt, )
# RNN前向传导与反向传播,获取梯度值
loss, dWxh, dWhh, dWhy, dbh, dby, hprev = lossFun(inputs, targets, hprev)
smooth_loss = smooth_loss * 0.999 + loss * 0.001
if n % 100 == 0: print 'iter %d, loss: %f' % (n, smooth_loss) # print progress
# 采用Adagrad自适应梯度下降法,可参看博文:http://blog.csdn.net/danieljianfeng/article/details/42931721
for param, dparam, mem in zip([Wxh, Whh, Why, bh, by],
[dWxh, dWhh, dWhy, dbh, dby],
[mWxh, mWhh, mWhy, mbh, mby]):
mem += dparam * dparam
param += -learning_rate * dparam / np.sqrt(mem + 1e-8) #自适应梯度下降公式
p += seq_length #批量训练
n += 1 #记录迭代次数参考文献:
1、http://www.wildml.com/2015/09/recurrent-neural-networks-tutorial-part-1-introduction-to-rnns/
2、http://blog.csdn.net/danieljianfeng/article/details/42931721
**********************作者:hjimce 时间:2015.10.23 联系QQ:1393852684 原创文章,转载请保留原文地址、作者等信息***************










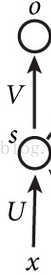
















 942
942

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








