OpenRoads Designer超高规则编辑对话框：超高过渡段选项设置

超高规则编辑对话框：超高过渡段选项（Runout and Transition Options）对话框设置如下图：

Runout and Transition Options这一栏主要是设置超高过渡段的实现方式。在此之前，我们先了解下面的基本概念：

• Runoff Length：指横坡从0%过渡到全超高所需要的长度。

• Runout Length：指从正常路拱过渡到0%横坡值所需要的长度。

超高过渡段长度指的是正常路拱过渡到全超高所需要的长度。

即Transition Length = Runout Length +Runoff Length，美国路线规范的超高过渡段仅包含Runoff Length，我想这应该是软件把Runout 和 Transition分开来说的原因。

《公路路线设计规范》(JTG D20-2017）（以下简称 规范）对超高过渡的规定：

7.5.6 超高过渡宜在回旋线全长范围内进行。当回旋线较长时，其超高过渡段应设在回旋线的某一区段范围内，超高过渡段的纵向渐变率不得小于1/330，全超高断面宜设在缓圆点或圆缓点处。

7.5.7 超高过渡段宜采用线性过渡方式。

规范中并没有规定从正常路拱过渡到0%横坡值所需要的长度为固定值，所以Runout Options下面的Fixed Length不勾选。

Non-Linear curve length：当Transition type不是线性（Linear）时会用到。

Present on tangent只有在没有缓和曲线，下面的Use Spiral Length 不勾选的情况下使用。

我们以下面的例子加以说明。

这段路线没有缓和曲线，并且超高过渡段长度是从正常路拱变化到全超高所需长度。那么我们需要设置Percent on Tangent 为0.8，并且把下面的Lengths are Total Transition勾上。如果超高过渡段长度是Runoff Length（从0%横坡变化到全超高所需长度），那么，Lengths are Total Transition不勾选。

Use Spiral Length：

• 勾选：超高过渡段长度为缓和曲线长；如果路线没有缓和曲线，超高过渡段长度需要计算。

• 不勾选：超高过渡段长度需要计算。

Start Inside Lane Rotation with Outside：

这个选项决定超高过渡方式。

• 勾选：内侧车道和外侧车道在同一桩号位置旋转，整个过程中，内侧车道和外侧车道不在一个平面上。

• 不勾选：外侧车道先旋转，达到反向路拱，此时内侧车道和外侧车道在一个平面上，然后内侧车道随外侧车道一起旋转。

Interpolate Table：

确定表格插值的取值。比如下面不同半径下超高的取值。

• 勾选：按插值取值。
• 不勾选：直接取大值。

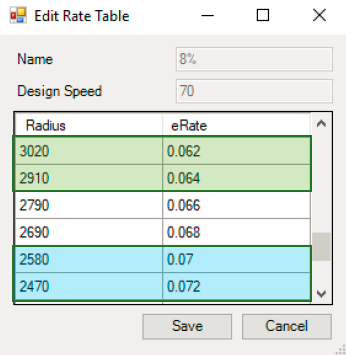
Radius	不勾选	勾选
3000	6.40%	6.24%
2500	7.20%	7.15%