《离散数学》期末练习题

《离散数学》期末练习题

一、填空题

1、若p，q为二命题，p→q真值为0 当且仅当 。
2、A={1,{2,3}}，则幂集P(A) = 。
3、对于公式x(P(x)∨Q(x))，其中P(x)：x=1，Q(x)：x=2，当个体域为{1,2}时，其真值为_______。
4、无向图为欧拉图的充要条件是 且图是连通的。
5、无向图G=<V,E>如下所示，则Δ(G)=________，δ(G)=__________。

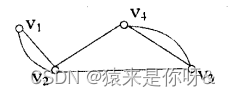
二、选择题

1、下列语句是命题的为（ ）。
A、我希望后天是晴天！；
B、；
C、2x>0当且仅当x大于0；
D、我正在说谎。
2、下列各项中，不是公式的是（ ）。
A、； B、；
C、； D、
3、下列选项中不成立的是（ ）。
A、若，则；
B、若，则；
C、若，则；
D、若，则。
4、下面各项中能构成图的度数列的是( )。
　 A、2,3,4,5,6,7； B、1,2,2,3,4；
C、2,1,1,1,2； D、3,3,5,6,0。
5、下列命题中不正确的是（　　）。

6、下列结果正确的是（ ）。

7、设G是连通平面图，有5个顶点，6个面，则G的边数是( )。
A、9条 B、5条
C、6条 D、11条.
8、设D的顶点数大于1，D=<V,E>是强连通图，当且仅当（　　）。
A、D中至少有一条通路
B、D中至少有一条回路
C、D中有通过每个顶点至少一次的通路
D、D中有通过每个顶点至少一次的回路

三、概念题

1、矛盾式（永假式）：
2、推理：
3、悬挂顶点与悬挂边:
4、欧拉通路:

四、计算题

1、用等值演算法或真值表法判断公式(p∨(q∧r))→(p∨q∨r)的类型；

2、(1) 已知图G有10条边, 4个3度顶点, 其余顶点的度数均小于等于2, 问G至少有多少个顶点?
(2)已知无向树T中, 有1个3度顶点, 2个2度顶点, 其余顶点全是树叶。试求树叶数。

六、应用题

设有a、b、c、d、e、f、g七个人，他们分别会讲的语言如下：a：英，b：汉、英，c：英、俄、西班牙，d：日、汉，e：德、西班牙，f：法、日、俄，g：法、德，能否将这七个人的座位安排在圆桌旁，使得每个人均能与他旁边的人交谈？ （提示：构造无向图，寻找一条Hamilton回路。）