题目:在一个二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
解题思路:从二维数组的右上角(或左下角)的元素开始判断,因为此元素是它所在行的最大数,是它所在的列的最小数。
如果它等于要查找的数字,则查找过程结束。
如果它大于要查找的数字,则可以排除它所在的列。
如果它小于要查找的数字,则可排除它所在的行。
这样如果要查找的数字不在数组的右上角,则每次判断都可以排除一行或一列以缩小查找范围,直到找到要查找的数字,或者查找范围为空。
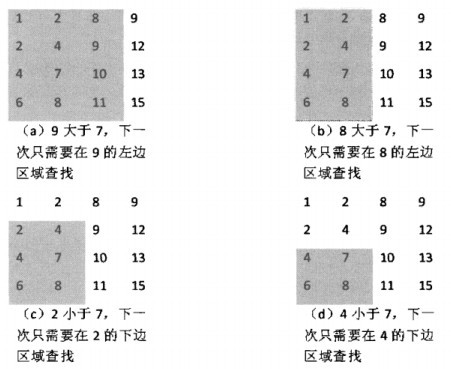
下图是在二维数组中查找7的示意图:
java代码实现:
public static void main(String[] args) {
int[][] arr = { { 1, 2, 8, 9 }, { 2, 4, 9, 12 }, { 4, 7, 10, 13 },
{ 6, 8, 11, 15 }, { 8, 10, 14, 17 } };
System.out.println(FindArray(arr, 5, 4, 8));// true
System.out.println(FindArray(arr, 5, 4, 22));// false
}
// rows--二维数组行数(arr.length)
// columns--二维数组列数(arr[0].length)
// number--要查找的数
public static boolean FindArray(int[][] arr, int rows, int columns,
int number) {
boolean found = false;
if (arr != null && rows > 0 && columns > 0) {
int row = 0;
int column = columns - 1;
while (row < rows && column >= 0) {
if (arr[row][column] == number) {
found = true;
break;
} else if (arr[row][column] > number) {
column--;
} else {
row++;
}
}
}
return found;
}2.旋转数组的最小数字(剑指offer-8)
题目:把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1.
解题思路:
1.我们用两个指针,分别指向数组的第一个元素和最后一个元素。按照题目旋转的规则,第一个元素应该是大于或者等于最后一个元素的(还有特例)。
2.接着我们得到处在数组中间的元素。如果该中间元素位于前面的递增子数组,那么它应该大于或者等于第一个指针指向的元素。此时数组中最小的元素应该位于该中间 元素的后面。我们可以把第一指针指向该中间元素,这样可以缩小寻找的范围。
3.如果中间元素位于后面的递增子数组,那么它应该小于或者等于第二个指针指向的元素。此时该数组中最小的元素应该位于该中间元素的前面。我们可以把第二个指针指向该中间元素,这样同样可以缩小寻找的范围。我们接着再用更新之后的两个指针,去得到和比较新的中间元素,循环下去。
按照上述的思路,我们的第一个指针总是指向前面递增数组的元素,而第二个指针总是指向后面递增数组的元素。最后第一个指针将指向前面子数组的最后一个元素, 而第二个指针会指向后面子数组的第一个元素。也就是它们最终会指向两个相邻的元素,而第二个指针指向的刚好是最小的元素。这就是循环结束的条件。
java代码:
public static int MinNumber(int[] numbers , int length)
{
if(numbers == null || length <= 0)
return 0;
int index1 = 0;
int index2 = length - 1;
int indexMid = index1;//旋转为0直接返回numbers[0]
while(numbers[index1] >= numbers[index2])
{
if(index2 - index1 == 1)
{
indexMid = index2;
break;
}
indexMid = (index1 + index2) / 2;
//如果下标为index1、index2和indexMid指向的三个数字相等,则只能顺序查找
if(numbers[index1] == numbers[index2] && numbers[indexMid] == numbers[index1])
return MinInOrder(numbers , index1 , index2);
if(numbers[indexMid] >= numbers[index1])
index1 = indexMid;
else if(numbers[indexMid] <= numbers[index2])
index2 = indexMid;
}
return numbers[indexMid];
}
//顺序查找
public static int MinInOrder(int []numbers , int index1 , int index2)
{
int result = numbers[index1];
for(int i = index1 + 1 ; i <= index2 ; ++i)
{
if(result > numbers[i])
result = numbers[i];
}
return result;
}
3.调整数组顺序使奇数位于偶数前面(剑指offer-14)
题目:输入一个整数数组,调整数组中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半部分。要求时间复杂度为O(n)。
解析:设2个头尾指针begin和end, begin从头往前遍历,遇到奇数的话,说明这个数在在正确的位置,所以继续往前遍历直到遇到第一个偶数。同样end指针从后往前遍历,遇到偶数的话,说明这个数在正确的位置,所以继续往前遍历,直到遇到第一个奇数。交换着2个数,然后继续上两步操作,只要满足begin<end;
// 调整数组顺序使奇数位于偶数前面
public static void Reorder(int[] pData, int length) {
if (pData == null || length == 0)
return;
int begin = 0;
int end = length - 1;
while (begin < end) {
while (pData[begin] % 2 == 1)
begin++;// 从前往后读到第一个偶数
while (pData[end] % 2 == 0)
end--;// 从后往前,读到第一个奇数
if (begin < end)// 这个if是有必要的,不然如果事先已经有序的话,奇偶数交界处的2个数会被调换过来
{
// 交换前面的第一个偶数和后面的第一个奇数
pData[begin] = pData[begin] ^ pData[end];
pData[end] = pData[begin] ^ pData[end];
pData[begin] = pData[begin] ^ pData[end];
begin++;
end--;
}
}
}后续: 数据结构---数组(2)























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








