重建二叉树

由前序遍历序列和中序遍历序列重建二叉树：

package leetCode;
import java.util.*;

public class BinaryTree {
	public static TreeNode Construct(int[] preOrder,int[] inOrder){
		int len=preOrder.length;
		if(preOrder==null||inOrder==null||len<=0) {
			return null;
		}
		return CoreConstruct(preOrder,0,len-1,inOrder,0,len-1);
	}
	public static TreeNode CoreConstruct(int[] preOrder,int startpreOrder,int endpreOrder,
			int[] inOrder,int startinOrder,int endinOrder)
	{
		//return null;
		int rootvalue=preOrder[startpreOrder];//前序遍历第一个节点的值为根节点
		TreeNode root=new TreeNode(rootvalue);
		root.left=null;
		root.right=null;
		if(startpreOrder==endpreOrder) {//递归基
			if(startinOrder==endinOrder&&preOrder[startpreOrder]==inOrder[startinOrder]) {
				return root;
			}
			else {
				System.out.println("Invalid input 2");
				//throw new Exception("Invalid input 1");
			}
		}
		//在中序遍历中找到根节点的值
		int rootinOrder=startinOrder;
		while(rootinOrder<=endinOrder&&inOrder[rootinOrder]!=rootvalue) {
			rootinOrder++;
		}
		//在输入两个序列不匹配的情况下
		if(rootinOrder==endinOrder&&inOrder[rootinOrder]!=rootvalue) {
			System.out.println("Invalid input 2");
		}
		
		int leftLength=rootinOrder-startinOrder;//获得左子树的长度
		int leftpreOrderEnd=startpreOrder+leftLength;//在前序遍历序列中确定左子树的长度
		//接下来在前序遍历序列中确定左子树和右子树的长度
		if(leftLength>0) {//构建左子树,如果左子树的长度大于0
			root.left=CoreConstruct(preOrder,startpreOrder+1,leftpreOrderEnd,inOrder,startinOrder,rootinOrder-1);
		}
		if(leftLength<endpreOrder-startpreOrder) {//只要左子树长度没有大于等于前序遍历序列的总长度，则说明还有右子树
			root.right=CoreConstruct(preOrder,leftpreOrderEnd+1,endpreOrder,inOrder,rootinOrder+1,endinOrder);	
		}
		return root;
	}
}
class TreeNode{
	int val;
	TreeNode left;
	TreeNode right;
	TreeNode(int x){val=x;}
}

根据前序遍历序列和中序遍历序列来重构二叉树

前序遍历：先访问跟节点，再访问左子树，接着访问右子树。

中序遍历：先访问左子树，再访问跟节点，接着访问右子树。

后续遍历：先访问右子树，再访问左子树，接着访问根节点。

 

过程：

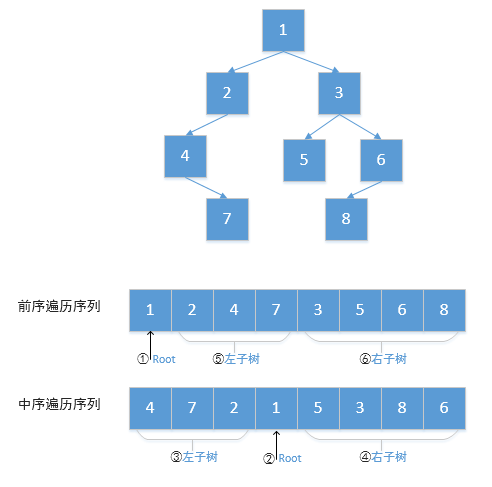
1.首先前序遍历第一个节点即为整个树的根节点。

2.接着在中序遍历序列中找到根节点所处的位置。

3.在中序遍历根节点所处的位置，左侧即为左子树，右侧即为右子树。分别算出左子树和右子树的长度。

4接着，回到前序遍历序列，根据左右子树的长度，在前序遍历序列中找到左右子树。5.这样我们就分别再次在前序遍历和中序遍历序列中划分了左右子树。

6.递归的分别构建左子树和右子树。之后再划分。

      

实现：

主函数：递归的调用辅助函数

1.     若前序或中序为空或长度小于0则返回null。

2.     递归调用辅助函数构造二叉树。

辅助函数：

1.     前序遍历序列的第一个节点为根节点。

2.     写递归基，如果前序初始节点序号等于结束节点序号，中序初始节点序号等于结束节点序号，并且前序初始节点值等于中序初始节点值。（总之，就是只有一个节点，并且前序中序节点值相等）。

3.     在中序遍历中找到根节点的值位置。

4.     如果在中序遍历序列中没有找到则抛出异常。

5.     得到左子树长度