poj 1127 Jack Straws 线段判交+并查集

最新推荐文章于 2020-02-07 15:21:14 发布

Bipedal_Bit

最新推荐文章于 2020-02-07 15:21:14 发布

阅读量1k

点赞数

分类专栏：解题报告文章标签： acm poj 计算几何线段相交并查集

本文链接：https://blog.csdn.net/bipedal_bit/article/details/44725461

版权

解题报告专栏收录该内容

18 篇文章 0 订阅

订阅专栏

Jack Straws

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 3277		Accepted: 1473

Description

In the game of Jack Straws, a number of plastic or wooden "straws" are dumped on the table and players try to remove them one-by-one without disturbing the other straws. Here, we are only concerned with if various pairs of straws are connected by a path of touching straws. You will be given a list of the endpoints for some straws (as if they were dumped on a large piece of graph paper) and then will be asked if various pairs of straws are connected. Note that touching is connecting, but also two straws can be connected indirectly via other connected straws.

Input

Input consist multiple case,each case consists of multiple lines. The first line will be an integer n (1 < n < 13) giving the number of straws on the table. Each of the next n lines contain 4 positive integers,x1,y1,x2 and y2, giving the coordinates, (x1,y1),(x2,y2) of the endpoints of a single straw. All coordinates will be less than 100. (Note that the straws will be of varying lengths.) The first straw entered will be known as straw #1, the second as straw #2, and so on. The remaining lines of the current case(except for the final line) will each contain two positive integers, a and b, both between 1 and n, inclusive. You are to determine if straw a can be connected to straw b. When a = 0 = b, the current case is terminated.

When n=0,the input is terminated.

There will be no illegal input and there are no zero-length straws.

Output

You should generate a line of output for each line containing a pair a and b, except the final line where a = 0 = b. The line should say simply "CONNECTED", if straw a is connected to straw b, or "NOT CONNECTED", if straw a is not connected to straw b. For our purposes, a straw is considered connected to itself.

Sample Input

Sample Output

CONNECTED 
NOT CONNECTED 
CONNECTED 
CONNECTED 
NOT CONNECTED 
CONNECTED
CONNECTED
CONNECTED
CONNECTED

==================================================================================================

题目大意：地上若干根木棍长短不一，木棍相互接触则算作相互连接，连接具有传递性，即间接连接也算连接。注意如果把木棍视为线段，有两种情况都视为木棍相互接触：

①线段相交（包括端点重合）；

②线段共线且有重叠部分。

输入数据（1组）：

木棍数（2~12）

木棍1：x1 y1 x2 y2（int型）

木棍2：x1 y1 x2 y2（int型）

...

木棍编号1 木棍编号2（1~木棍数）

...

某对木棍编号为“0 0”则结束本组查询。

某组木棍数为0则结束程序。

输出数据：

每接收一对木棍编号，判断连接，输出“CONNECTED”或“NOT CONNECTED”。

解题思路：看到连接具有传递性就该想到木棍将组成集合，判断连接即判断木棍是否属于同一个集合，用并查集再方便不过了。然后是决定并查集合并集合的条件，也就是上面提到的两种情况：线段相交和共线重叠。

判断线段相交，有一个典型算法：快速排斥+跨立实验。

①快速排斥：

设以线段 P1P2 为对角线的矩形为R，设以线段 Q1Q2 为对角线的矩形为T，如果R和T不相交，显然两线段不会相交。

②跨立实验：
（下面的公式中*代表点积，×代表叉积）

如果两线段相交，则两线段必然相互跨立对方。
若P1P2跨立Q1Q2 ，则矢量 ( P1 - Q1 ) 和( P2 - Q1 )位于矢量( Q2 - Q1 ) 的两侧，
即( P1 - Q1 ) × ( Q2 - Q1 ) * ( P2 - Q1 ) × ( Q2 - Q1 ) < 0。
上式可改写成( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) > 0。
当 ( P1 - Q1 ) × ( Q2 - Q1 ) = 0 时，说明 ( P1 - Q1 ) 和 ( Q2 - Q1 )共线，但是因为已经通过快速排斥试验，所以 P1 一定在线段 Q1Q2上；
同理，( Q2 - Q1 ) ×(P2 - Q1 ) = 0 说明 P2 一定在线段 Q1Q2上。
所以判断P1P2跨立Q1Q2的依据是：( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) >0。
同理判断Q1Q2跨立P1P2的依据是：( Q1 - P1 ) × ( P2 - P1 ) * ( P2 - P1 ) × ( Q2 - P1 ) >0。

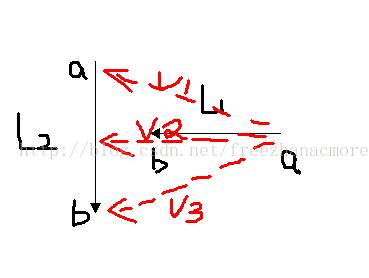
下面以直线的跨立实验详细说明下：

PS：直线可以无限延长，所以如果 L1 跨立了 L2，那么L2 必定跨立 L1, 那么 L1 与 L2 必然相交

线段就要判断 L1 跨立 L2 并且 L2 跨立 L1 才能说明二者相交。

如图所示：直线 L2 跨立了直线 L1, L2与 L1 必然相交，但是如果它们是线段的话，是不相交的。

cross(V1, V2) 代表向量 V1和 V2的叉积。

注意到 V1 偏向 V2 和 V2 偏向 V3 的方向是相同的，如果偏转的方向相同，那么说明他们的叉积必定同为正或者同为负。

当然上面的这个图自己比划一下就可以知道cross(V1, V2) 是为正的，所以如果 cross(V1,V2)*cross(V2, V3) > 0 那么说明 L2 跨立 L1。

我写这道题时刚开始只用了跨立实验，没做快速排斥，但是后来发现忽略了共线的情况，于是共线的线段做了是否重叠的特殊判断，衍生出了跨立实验+共线特判的套路。

典型套路和我使用的套路各有利弊，请大家视情况自行选择。有心的同学可以试试用典型套路交能不能快一些。

#include <cstdio>

/**
* 三维向量
*/
struct V
{
    double x;
    double y;
    double z;
    V(double X, double Y, double Z):x(X),y(Y),z(Z){}
    double operator *(const V &b)const//向量点乘
    {
        return x*b.x+y*b.y+z*b.z;
    }
};

/**
* 二维点
*/
struct P
{
    int x;
    int y;
    P(){}
    P(int X, int Y):x(X),y(Y){}
    V operator -(const P &b)const//点->向量
    {
        return V(x-b.x,y-b.y,0);
    }
};

const int LINE_MAX = 15;
/**
* 二维线段
*/
struct L
{
    P a;
    P b;
    L(){}
    L(P A, P B):a(A),b(B){}
}line[LINE_MAX];

V vecCross(V a, V b)//向量叉乘
{
    return V(0,0,a.x*b.y-b.x*a.y);
}

bool segment(L p, L q)//判断线段是否跨立或重叠
{
    V v1 = p.a-q.a;
    V v2 = q.b-q.a;
    V v3 = p.b-q.a;
    V c1 = vecCross(v1,v2);
    V c2 = vecCross(v2,v3);
    double tmp = c1*c2;
    double absTmp = tmp < 0?-tmp:tmp;
    if( absTmp < 1e-5 )//判断共线线段是否有重叠部分，( P1 - Q1 ) × ( Q2 - Q1 ) = 0做了精度处理
    {
        int pMax = p.a.x;
        int pMin = p.b.x;
        int qMax = q.a.x;
        int qMin = q.b.x;
        if( p.a.x < p.b.x )
        {
            pMax = p.b.x;
            pMin = p.a.x;
        }
        if( q.a.x < q.b.x )
        {
            qMax = q.b.x;
            qMin = q.a.x;
        }
        if( pMin > qMax || pMax < qMin )
            return false;
        return true;
    }
    return tmp > 0;//判断不共线线段是否跨立
}

bool cross(L p, L q)//线段相交
{
    return segment(p,q)&&segment(q,p);
}

//并查集
const int CASE_MAX = 13;
int father[CASE_MAX];
int getFather(int x)//x为根则其父亲为自己，否则递归寻找父亲并将沿路同一个集合的元素指向同一个根
{
    return (!father[x])?x:( father[x] = getFather(father[x]) );
}
void _union( int x , int y )//将两个元素所在集合合并
{
    int fx = getFather(x);
    int fy = getFather(y);
    if( fx != fy )
        father[fy] = fx;
}

int main()
{
    int t;
    while( scanf("%d", &t), t )
    {
        for( int i = 0 ; i < LINE_MAX ; i++ )//初始化父亲数组
            father[i] = 0;
        int lineCnt = 1;
        while( t-- )//输入边
        {
            int x, y;
            scanf("%d%d", &x, &y);
            P p1 = P(x,y);
            scanf("%d%d", &x, &y);
            P p2 = P(x,y);
            line[lineCnt++] = L(p1,p2);
        }
        for( int i = 1 ; i < lineCnt ; i++ )//根据边相交情况划分边的集合
            for( int j = i+1 ; j < lineCnt ; j++ )
                if( cross(line[i],line[j]) )
                    _union(i,j);
        int no1, no2;
        while( scanf("%d%d", &no1, &no2) )//判断是否同集合并输出答案
        {
            if( !no1 || !no2 )
                break;
            bool ok = (getFather(no1) == getFather(no2));
            printf("%s\n", ok?"CONNECTED":"NOT CONNECTED");
        }
    }
    return 0;
}



/**************************************
Memory: 352K		Time: 63MS
Language: G++		Result: Accepted
**************************************/

/***********测试数据*************
8
0 0 1 0
3 0 3 1
4 0 4 1
5 0 6 0
4 0 5 0
3 0 4 0
2 0 3 0
1 0 2 0
(这些应该互相全CONNECTED,出NOT就错)

3
1 1 2 2
3 3 4 4
0 0 1 0
(这些互相全NOT CONNECTED,注意#1 #2共线且不相交)

2
0 2 0 0
0 0 1 0
(题里给的数据,共线相交）
 ******************************/