AcWing 3959：天然气管道 ← 曼哈顿距离

【题目来源】
https://www.acwing.com/problem/content/3962/

【题目描述】
某市有 n 个采气点和 n 个配气站。
现在，要给它们一一配对，每个采气点搭配一个配气站，它们之间用天然气管道连接，从而实现天然气供给。
已知，管道建设必须由采气点开始，且管道必须沿正东（x 轴正方向）或正南（y 轴负方向）方向铺设。
为了解决成本，天然气管道的总长度越短越好。
请计算，天然气管道的最短总长度。

【输入格式】
第一行包含整数 n。
接下来 n 行，每行包含两个整数 x，y，表示一个采气点的坐标为 (x, y)。
最后 n 行，每行包含两个整数 x，y，表示一个配气站的坐标为 (x, y)。

【输出格式】
一个整数，表示天然气管道的最短总长度。

【数据范围】
2≤n≤50000 ,
0≤x, y≤10^5。

【输入样例】
3
3 5
1 2
4 3
6 3
5 2
2 1

【输出样例】
9

【样例解释】

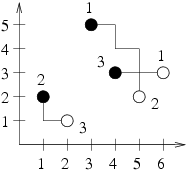
【算法分析】
● 本题乍一看，以为是寻求最优匹配。但仔细分析，发现并没有那么复杂。分析过程如下：
（1）根据题意，由于采气点与配气站一一配对，且管道建设必须由采气点开始，沿正东或正南方向铺设，所以配对成功的采气点 s 与配气站 e 必然满足“配气站的横坐标大于等于采气点的横坐标，配气站的纵坐标小于等于采气点的纵坐标”，则其曼哈顿距离计算公式为 s.y-e.y+e.x-s.x。
（2）不失一般性，设 s1、s2 是任意两个采气点，e1、e2 是任意两个配气站。则由 s1、s2 及 e1、e2 可得如图所示的两种组合及各自的曼哈顿距离计算式。

仔细观察示意图易得，不管哪种组合，其计算曼哈顿距离的式子是相同的。所以本题不需复杂的算法，只需简单的加减运算即可。

【算法代码】

#include <bits/stdc++.h>
using namespace std;

int n;
int x,y;
long long ans;

int main() {
    cin>>n;
    for(int i=1; i<=n; i++) {
        cin>>x>>y;
        ans-=x, ans+=y;
    }
    for(int i=1; i<=n; i++) {
        cin>>x>>y;
        ans+=x, ans-=y;
    }
    cout<<ans<<endl;

    return 0;
}

/*
in:
3
3 5
1 2
4 3
6 3
5 2
2 1

out:
9
*/

【参考文献】
https://www.cnblogs.com/guangheli/p/10959879.html
https://www.cnblogs.com/Ch-someone/p/9724806.html
https://blog.csdn.net/m0_72853403/article/details/129374047