Problem E: 积木积水
Description
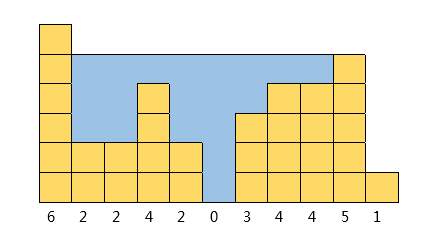
现有一堆边长为1的已经放置好的积木,小明(对的,你没看错,的确是陪伴我们成长的那个小明)想知道当下雨天来时会有多少积水。小明又是如此地喜欢二次元,于是他把这个三维的现实问题简化成二维的问题。设雨量无穷、积木不透水、积木间无缝连接,问在这个二次元的世界里,已放置好的积木会有多少单位的积水量?
Input
第一行包含一个整数T(T≤100),表示接下来的测试样例个数。 每个测试样例有两行组成: 第一行包含一个整数N(N≤1e6),表示积木的列数; 第二行包含N个整数Ai(Ai≤1e6),表示第i列积木的个数。
Output
每个样例输出一行,包含一个整数,为题目所求。
Sample Input
1
11
6 2 2 4 2 0 3 4 4 5 1
Sample Output
19
HINT
来源: http://gdutcode.sinaapp.com/problem.php?cid=1039&pid=4
#include <bits/stdc++.h>
using namespace std;
#define MAXN 1000000
int A[MAXN+1];
long long ans;
void CAL(int lef,int rig) //产生W结构时且W中点大于任一端点则分治,否则直接计算
{
int L_max=A[lef],R_max=A[rig],MAX= -20,LOC_max=0;
for(int i=lef+1;i<=rig-1;i++)
if(MAX<A[i]) { MAX=A[i];LOC_max=i; }
LOC_max = (A[LOC_max]>=L_max||A[LOC_max]>=R_max)?LOC_max:0;
if(LOC_max) {CAL(lef,LOC_max);CAL(LOC_max,rig);return;}
else
{
int ave=min(A[lef],A[rig]);
for(int i=lef+1;i<=rig-1;i++) ans+=(ave-A[i]);
}
return;
}
int main()
{
int T;scanf("%d",&T);
for(int i=1,n,j;i<=T&&scanf("%d",&n);i++)
{
int lef,rig;
for(j=1;j<=n;j++) scanf("%d",&A[j]);
for(j=1;j<=n&&A[j]<=A[j+1];j++); lef=j;//去掉左端递增项
for(j=n;j>=1&&A[j]>=A[j-1];j--); rig=j;//去掉右端递减项
ans=0;CAL(lef,rig);
printf("%I64d\n",ans);
}
return 0;
}





















 4388
4388











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








